Parallax (Greek παραλλλάξ , from παραλλλαγή , “change, alternation”) is a phenomenon where the apparent position of an object changes relative to a distant background based on the observer’s position.
To determine the distance to the object, one can use the known distance between the observation points D (base) and the offset angle α in radians:

Parallax is commonly employed in geodesy and astronomy to measure the distance to distant objects, particularly in parsecs. It is also the fundamental principle behind binocular vision.

Astronomy
Daily Parallax
The daily parallax, also known as geocentric parallax, refers to the difference in directions to the same celestial object as observed from the Earth’s center of mass (geocentric direction) and from a specific point on the Earth’s surface (topocentric direction).
Due to the Earth’s rotation around its axis, the position of the observer changes cyclically. At the equator, the parallax base is equivalent to the Earth’s radius, which is approximately 6371 km.
When observing the Moon, its apparent displacements against the backdrop of stars (compared to the calculated orbital motion) can reach up to 2 degrees (corresponding to a parallax of 1 degree). Ancient Greek astronomers were the first to notice these displacements, which allowed them to accurately determine the distance to the Moon.
The planets’ daily parallax is quite small (only 24″ for Mars during the great opposition), but it was the primary method of measuring absolute distances in the Solar System before radar became available. The most convenient events for this purpose were Venus passing across the Sun’s disk and asteroids that came close to Earth. Relative distances can be easily determined based on Kepler’s laws, so measuring just one distance is enough to determine all of them.
Yearly parallax
The yearly parallax is the measurement of the angle at which the Earth’s orbit, with its major semi-axis perpendicular to the star’s direction, is observed from the star.
Yearly parallaxes serve as indicators of star distances. A distance with a yearly parallax equal to 1 arc second is known as a parsec (1 parsec = 3.085678-10 16 m). The closest star, Proxima Centauri, has a parallax of 0.77″, which means its distance is 1.298 pc.
Centennial parallax
Centennial parallax refers to the phenomenon where the apparent position of an object on the celestial sphere changes due to a combination of its proper motion and the motion of the solar system within the galaxy.
Parallax in photography
Viewfinder parallax


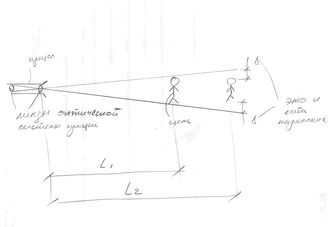
The phenomenon of viewfinder parallax occurs when there is a discrepancy between the image observed through an optical non-mirror viewfinder and the resulting image captured in a photograph. Parallax is typically negligible when shooting subjects at a distance, but becomes increasingly significant when photographing subjects up close. This discrepancy is caused by the difference in distance (known as the basis) between the optical axes of the lens and the viewfinder. The specific value of parallax can be calculated using the following formula:

The distance (basis) between the optical axes of the lens and viewfinder is known as  . Additionally, the focal length of the camera lens is an important factor. Another crucial factor is the distance to the pointing plane (shooting object), which is represented by
. Additionally, the focal length of the camera lens is an important factor. Another crucial factor is the distance to the pointing plane (shooting object), which is represented by  .
.
Parallax of the Viewfinder (Sighting Plane)
When it comes to the viewfinder, parallax is a unique phenomenon. It is not simply the difference in height between the sight axis and the barrel axis, but rather the discrepancy in distance between the shooter and the target.
Parallax in Rangefinders
Parallax in rangefinders refers to the angle at which an object appears when focusing with an optical rangefinder.
Parallax in Stereoscopic Vision
Parallax in stereoscopic vision pertains to the angle at which an object is perceived when viewed with both eyes or captured with a stereoscopic camera.
Temporal parallax
Temporal parallax refers to the phenomenon of object shape distortion that occurs when capturing images with a camera equipped with a curtain shutter. This distortion is a result of the sequential exposure of different parts of the photosensitive element as the shutter slit moves. As a consequence, the shape of fast-moving objects may appear distorted in the captured image. For instance, if an object moves in the same direction as the shutter slit, its image will be stretched, whereas if it moves in the opposite direction, it will appear narrowed.
Historical Background
In the realm of scientific inquiry, Galileo Galilei put forth the hypothesis that if the Earth were to revolve around the Sun, a phenomenon known as parallax would manifest itself in the form of impermanence, particularly when it comes to distant stars.
The initial endeavors to observe the yearly parallax of stars proved fruitful when V. J. Struve successfully accomplished this task for Vega (α Lyra) in 1837. The findings were then documented and published. However, it was not until 1838 that truly reliable measurements of the annual parallax were obtained by F. W. Bessel, specifically in relation to the star 61 Swan. Bessel is duly credited with the priority of the discovery of the annual parallax of stars.
Related Content
Recommended Readings
- Yashtold-Govorko V. A. Photography and image processing. Photography techniques, formulas, terminology, recipes. 4th Edition, condensed – Moscow: “Art”, 1977.
Additional Resources
How can we measure the distance to the stars? The parallax method relies on the observation that when viewed from different positions on Earth’s orbit, nearby objects appear to move faster than distant ones. By measuring the slight change in the observer’s position, we can determine that the nearest stars are millions of times farther from Earth than the Sun. Most of these stars are located in the disk-shaped structure that forms our Galaxy, which is visible as a band in the sky known as the Milky Way.

Once it was evident that the stars were not mere openings in glass orbs but rather countless far-off suns, the inquiry emerged regarding their distance. The configurations in which the distant stars are organized are referred to as constellations – such as the hunter Orion, the Big Dipper, and the Southern Cross. However, it required ages to comprehend how these stars are positioned in the vast expanse of space.
One indication is the uneven distribution of stars in the sky, with the majority of them concentrated in the luminous belt known as the Milky Way. This belt appears brightest in the Southern Hemisphere, particularly near the constellation Sagittarius, where dark clouds and luminous nebulae create a captivating celestial scene. Presently, it is understood that the Milky Way consists of billions of faint stars that blend together to form a faint glow when observed with the naked eye. By mapping the positions of these stars, it becomes apparent that they are organized into spiral arms. Our Sun resides within one of these spiral arms, akin to a peaceful suburban neighborhood within our galaxy. But how was this determined?
Angular seconds
Scientists in the field of astronomy utilize projections of angles to determine distances in the celestial realm. The approximate measurement of the Moon’s size equates to half a degree. A degree is further partitioned into 60 angular minutes (´), which are then subdivided into 60 angular seconds (´´). Remarkably, an angular second is equivalent to 1/3600 of a degree.
The Milky Way Galaxy

The Milky Way, known as Via Lactea in Latin, has long been a subject of fascination for ancient civilizations. Greek philosophers such as Aristotle and Anaxagoras believed that it consisted of a vast expanse of burning stars, but lacked the means to verify this hypothesis. It was not until 1610, when Galileo turned his telescope towards the heavens, that the veil of uncertainty was lifted and individual stars became discernible.
The distribution of stars in the vast expanse of the cosmos was a topic pondered by philosopher Immanuel Kant. In his treatise from 1755, he argued that the stars within the Milky Way are arranged in a colossal disk, held together by the force of gravity – similar to the way planets in our solar system orbit the sun in a single plane. The stars appear as a band in the sky because of our position within this disk.

During the year 1785, an astronomer from Britain named William Herschel conducted a thorough examination of the structure of the Milky Way by carefully observing numerous stars. As he plotted the positions of these stars, he came to the realization that there was a higher concentration of stars in a specific region of the sky. Herschel proposed the idea that the Sun is located on the disk of the Milky Way, challenging the previous belief that it was positioned at the center.

In a distant realm
Even though it was previously believed that all stars were positioned at an equidistant distance from our planet, astronomers have gradually come to acknowledge the unlikelihood of this assumption. It is evident that stars are not uniformly dispersed. Isaac Newton’s theory of gravitation proposed that if stars possessed enough mass, they would be attracted to one another, similar to how planets are pulled towards the sun. However, given that stars are not clustered together, it appears that this gravitational force is not sufficiently strong. As a result, stars are positioned at significant distances from each other. By contemplating in this manner, Newton became one of the first individuals to fathom the immense remoteness of stars.
Astronomers have sought ways to determine the distance to a specific star. One approach involves measuring its brightness: if a star’s brightness is similar to that of the Sun, it should decrease in proportion to the square of the distance. Utilizing this assumption, the Dutch physicist Christian Huygens (1629-1695) computed the distance to Sirius, the brightest star in the night sky. He carefully selected the size of a small aperture in a screen so that it allowed an amount of sunlight equivalent to the light emitted by Sirius. By comparing the size of the aperture to the size of the Sun, he inferred that Sirius must be tens of thousands of times farther away. Later, Newton estimated that Sirius was a million times more distant than the Sun by comparing its brightness to that of Saturn. Newton’s estimate was nearly accurate: Sirius is actually located at approximately half that distance. Thus, the vastness of interstellar space was unveiled.


"If I have observed a greater distance than others, it is because I have been supported by the knowledge and discoveries of those who came before me" Isaac Newton, in a correspondence with Robert Hooke (1676)
Parsecs
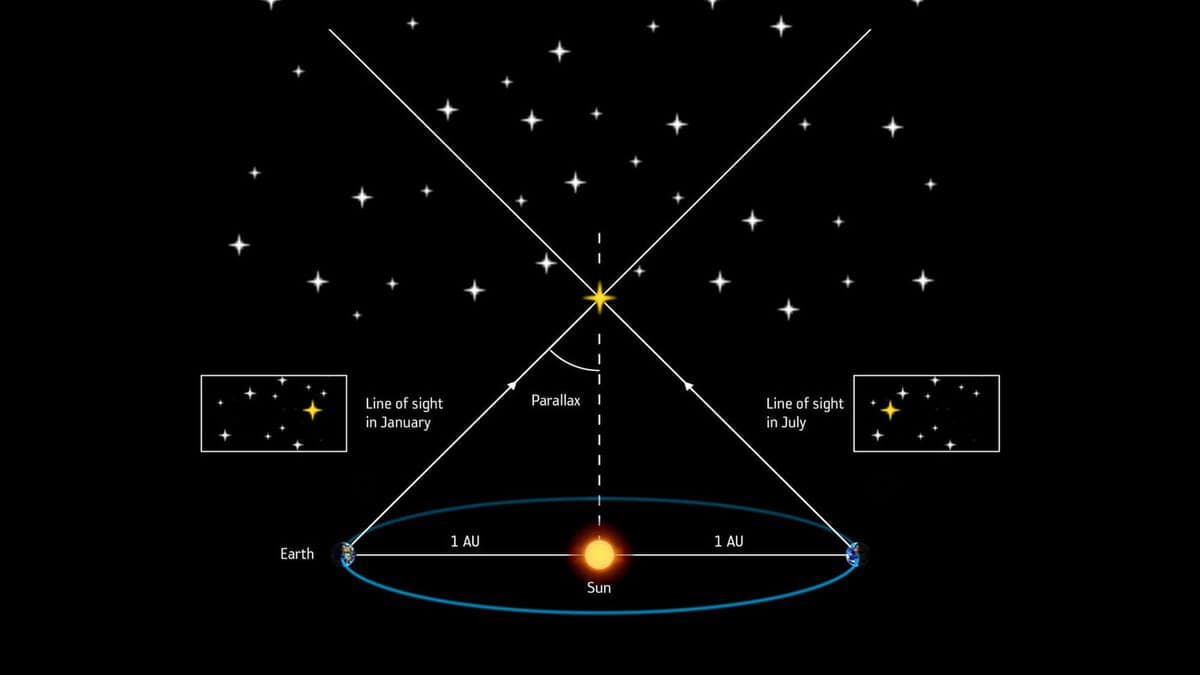
The concept of stellar parallax in astronomy refers to the measurement of the apparent shift in the position of a star when viewed from different vantage points, such as Earth and the Sun. Specifically, it represents the angle at which the average radius of Earth’s orbit would be observed from the star’s center of mass. A unit of measurement known as a parsec, which is equivalent to 3.26 light-years, is defined based on this parallax being one arc second.
Parallax
However, the brightness of stars varies and is not always the same as that of the Sun.
In 1573, Thomas Diggs, an astronomer from Britain, proposed the application of the parallax method, commonly used in geography, to study stars. Parallax refers to the change in the angle at which an object is perceived as it is observed from different positions. For example, when traveling across a country, the direction to a nearby hill changes more rapidly compared to that of a distant mountain. Similarly, while driving a car, the trees closer to you appear to pass by at a faster rate than those that are further away. The apparent positions of stars as observed from Earth are also affected by the elliptical orbit of our planet around the Sun, and the magnitude of this shift depends on the distance between us and the stars.
Astronomers were quick to investigate these yearly movements of stars – to calculate their distance and verify the heliocentric model of the solar system. However, during this process, they made an unexpected discovery. In 1674, Robert Hooke published data regarding the movement of the gamma star of Draco, a brilliant star that crosses directly over London’s latitude. Hooke was able to make precise observations by creating a special aperture in the roof of his own house. In 1680, Jean Picard reported that Polaris was shifting by 40 angular seconds per year, a finding that was later confirmed by John Flamsteed in 1689.
Curious to decipher the meaning of these alterations, James Bradley replicated the observations and documented the Dragon gamut’s seasonal shifts – in 1725 and 1726. However, these shifts differed from parallax: the magnitude of the shift should have been dependent on the distance to the star, but all the observed stars manifested the same type of shift.
Bradley found himself perplexed by this phenomenon. After a couple of years, he had an epiphany: just as a weathervane on a mast adjusts its direction as the ship turns, displaying the combined effect of the wind and the ship’s movement, the Earth’s motions alter our perspective of the stars. As we revolve around the Sun, all the stars exhibit a slight wobble. This unforeseen revelation, known as stellar aberration, also serves as confirmation of the Earth’s orbit around the Sun.
Parallax was only discovered when instruments became precise enough to detect it. The first successful measurements were conducted by Friedrich Bessel in 1838, specifically for star 61 in the constellation Swan. Due to the vast distances of stars, their parallax is extremely small and challenging to measure. As an example, the parallax of our closest star, Proxima Centauri, is less than one arcsecond, which is 50 times smaller than its aberration. In the present day, satellites like the European Space Agency’s Hipparchus have accurately determined the positions of 100,000 nearby stars, enabling the calculation of distances to many others. However, parallax can only be observed at distances within approximately 1% of the size of our Galaxy.
Robert Hooke, born in 1635 and died in 1703.


The Earth is not a stationary object in space. It rotates on its axis every 24 hours, creating a day and night cycle. Additionally, it orbits around the Sun, completing one revolution in 365 days, which is known as a year.
Overview
The Earth’s orbit has a radius of approximately 150 million kilometers, which is equivalent to one astronomical unit. As a result, all celestial objects in the Earth’s sky also undergo annual “loops” or parallactic motion. The farther a celestial object is from the Earth, the less noticeable its parallactic motion becomes in the Earth’s sky. The term “parallax” comes from the Greek word meaning “displacement.”
Historical Background
The concept of diurnal (geocentric) parallax refers to the measurement of the Earth’s radius as observed from a specific celestial body. Another related concept is horizontal parallax, which measures the angle at which the equatorial radius of the Earth is seen from the center of a celestial body when it is positioned at the true horizon. The true horizon is a conceptual circle on the celestial sphere that is perpendicular to the plumb line at the observer’s location. The differences between diurnal and horizontal parallax can be attributed to the Earth’s non-spherical shape, with the polar radius being 21 km shorter than the equatorial radius.
The diurnal parallax has played a significant role throughout the history of astronomy as it is the simplest and most reliable method for determining distances to objects in the Solar System. In fact, it was the only geometric method available for measuring distances in the Solar System until radar, laser ranging, and radio interferometry techniques were developed for interplanetary missions. The Earth’s radius serves as the baseline for calculating the diurnal parallax. The Moon (with a diurnal parallax of 57 angular minutes) and the Sun (with a diurnal parallax of 9 angular minutes) have the largest values. For all the planets in the Solar System, the diurnal parallax undergoes regular changes and is much smaller than an angular minute. Venus has a range of 0.1-0.6 angular minutes, Mars has a range of 0.1-0.4 angular minutes, Jupiter and Saturn have less than 0.1 angular minutes, and Uranus and Neptune have less than one angular second.
The parallax of the Moon and Sun was first determined by ancient Greek astronomers through observations of lunar eclipses, allowing them to calculate the parallax of the Moon from a single location. In 129 BC, the ancient Greek astronomer Hipparchus of Nicaea (180-125 BC) estimated the parallax of the Sun to be 7 angular minutes, the highest angle that could not be discerned by the naked eye. Prior to Hipparchus, another ancient Greek astronomer, Aristarchus of Samos (310-230 B.C.), had also conducted similar calculations.
However, Claudius Ptolemy, an astronomer from Alexandria who lived from 100-170 AD, held a different belief. He thought that the distance to the Moon was influenced by its phases. This caused a significant disagreement among astronomers in the ancient world regarding the estimates of the Moon’s and the Sun’s parallaxes. Ptolemy’s mistake regarding the correlation between the size of the Moon’s parallax and its phases later became a major point of criticism for the Ptolemaic world system. Nicolaus Copernicus, a young scholar born in 1473 and died in 1543, measured the Moon’s parallax while he was studying in Italy under the guidance of his teacher Novara. On March 9, 1497, during an eclipse of the bright star Aldebaran in Bologna, observations of the Moon’s position revealed that its parallax was not influenced by its phase. In the following centuries, simultaneous observations from the northern and southern hemispheres became common practice in accurately measuring the parallaxes of the Moon, Sun, and Mars. For instance, in the 18th century, such observations were conducted at the Cape of Good Hope Observatory in southern Africa and the Berlin Observatory.
Comparison between the heliocentric and geocentric models of the universe
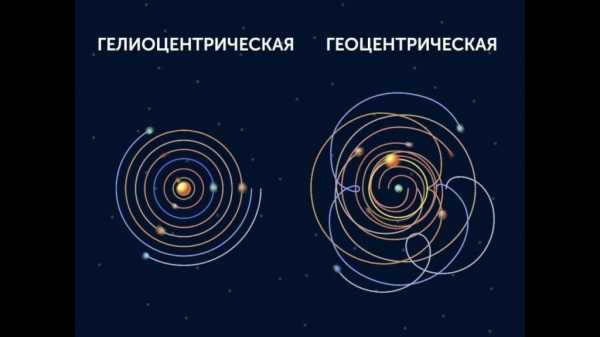

The heliocentric and geocentric world systems are being compared.
Vasily Struve and the Pulkovo Observatory where he was employed

In the years 1837-1838, three researchers, namely Basil Struve (1793-1864), Friedrich Bessel (1784-1846), and Thomas Henderson (1798-1844), made the first reliable measurements of stellar parallaxes. Struve calculated the parallax of the star Vega, Bessel measured that of 61 Swan, and Henderson determined the parallax of Alpha Centauri. However, as early as 1822, Friedrich Struve, working at the Derpt Observatory in present-day Estonia, had already obtained fairly accurate measurements of the parallaxes of several bright stars, such as Altair.
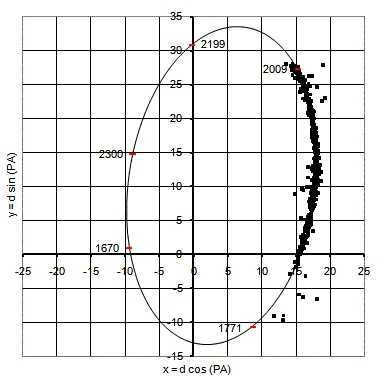
The 61 Swan system displays the orbital motion of stars, with astronomers’ measurements depicted by black marks.
Furthermore, there was an earlier publication by French astronomer Dominique Arago (1786-1853) that provided the parallax value for 61 Swan, though it contained a significant error. However, F. Bessel’s results, which were based on over 400 astrometric measurements, were widely accepted as the most reliable by the global scientific community.
By contrast, Vega was only measured astrometrically 17 times by F. Struve. Furthermore, Bessel’s research was made easier by the fact that the binary system 61 Cygni exhibited observable orbital movement. This allowed for a comparison of the parallaxes of both stars in the system.
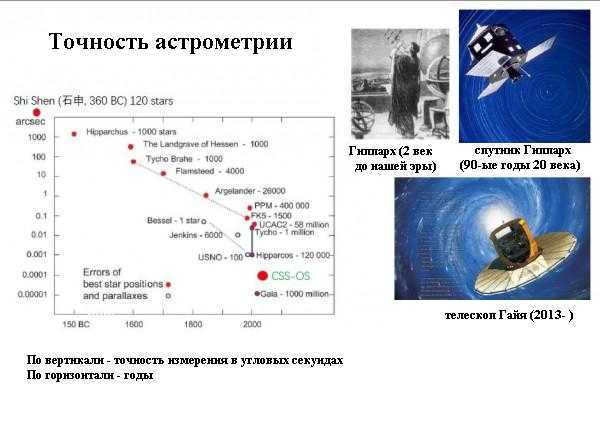
Advancements in the precision of determining the positions of stars have significantly improved over the past 2.5 millennia.
The fundamentals of geometry and trigonometry
When computing the lunar parallax, the principles of geometry heavily rely on a right-angled triangle. A right-angled triangle is a triangle that contains one angle measuring 90 degrees.
In a right triangle, the two sides that create a 90-degree angle are referred to as the catheti, while the side opposite the 90-degree angle is known as the hypotenuse. The total of all angles in a right triangle amounts to 180 degrees. Based on this information, it is possible to determine that with a given cathetus (the Earth’s radius) and the angle between the hypotenuse and the cathetus (daily parallax), the length of the hypotenuse (distance to the celestial body) can be calculated by dividing the known cathetus by the sine of the daily parallax.
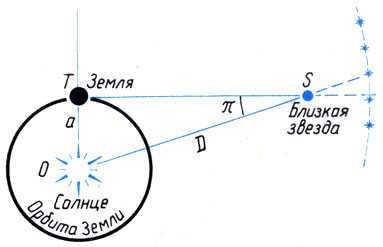

In this scenario, the radius of the Earth’s orbit around the Sun takes the place of the Earth’s radius, while the annual parallax replaces the diurnal parallax
The sine function in a right triangle represents the ratio of the side opposite the given angle to the hypotenuse.
A similar method is used to calculate trigonometric distances to stars.
Due to the vast distances between stars (with the closest star being 270 thousand astronomical units away from the Sun), the most common method for calculating trigonometric distances involves utilizing the ratio of 206265 angular seconds and the measured annual parallax, which is also expressed in angular seconds. The value 206265 represents the number of angular seconds in a single radian. A radian is defined as the angle that corresponds to the arc of a circle with a length equal to the radius of that circle.
Specific examples of the application of daily and annual parallax
For countless millennia, the Solar System was believed to consist of only nine known objects, including Earth, Moon, Sun, Mercury, Venus, Earth, Mars, Jupiter, and Saturn. This belief remained unchallenged until the occasional appearance of comets in the inner regions of the Solar System. However, in the 18th century, astronomers made groundbreaking discoveries by identifying new planets and asteroids, such as Uranus and Ceres. These new findings prompted astronomers to devise methods for calculating the orbits of celestial bodies within the Solar System using the fewest possible measurements. In 1801, the brilliant German mathematician Friedrich Gauss (1777-1855), at just 24 years old, developed a mathematical technique to locate the elusive Ceres. This revolutionary method allowed for the determination of the celestial body’s orbit based on only three observations.
Simultaneously, it is possible to calculate the approximate distance to a celestial entity within the Solar System based on only two observations. This is particularly applicable when it comes to detectable entities located beyond the orbit of Neptune (TNO). In the case of such entities, their motion speed is minimal in comparison to the Earth’s orbital speed (a few hundred meters per second versus 30 km per second). Consequently, the observed distance from the Sun (heliocentric distance) to TNOs in astronomical units can be determined by the straightforward ratio of 150/q, where q represents the object’s angular velocity in angular seconds within one hour.

Recently, the VLBA radio interferometer achieved a remarkable feat in radio astronomy by measuring the farthest parallax ever recorded. They determined that the interstellar cloud G007.47+00.05, located in the outer arm of Shield-Centaurus, is situated at a distance of 20 thousand parsecs or 67 thousand light years.
Parallaxes beyond our galaxy
In the constellation Sagittarius, the Solar System is just one of the many planetary systems that orbit around the center of our galaxy. It takes approximately 225-250 million years for the Solar System to complete one revolution around the galactic center, also known as a galactic year. The average speed of the Solar System in interstellar space is about 220 km per second. Due to variations in galactic orbits, the trajectories, angular velocities, and spatial velocities of other stars in our sky differ from those of Earth.
As mentioned previously, the discovery of stars’ proper motions was first made by the English astronomer Edmond Halley (1656-1743) in 1718. This important finding occurred a hundred years before the first parallax measurements, making stars with high proper motions particularly intriguing for such measurements. Two out of the three initial parallaxes published in 1837-1838 were obtained from stars with high proper motion (61 Swan and Alpha Centauri). These systems have a proper motion of approximately 4 angular seconds per year. To put this into perspective, the third star Vega has a much lower proper motion, which is 20 times less (F. Bessel selected Vega for parallax measurements due to its exceptional brightness in the northern sky). In the subsequent years, the search for unknown nearby stars typically began with the identification of stars with high proper motion (for instance, this is how Proxima Centauri and Barnard’s Star were discovered in the 20th century). Consequently, astronomers have recently started to discover nearby star systems with minimal proper motion (0.15 angular seconds per year or even less). However, it’s worth noting that this trend may not hold true for dense star fields or areas close to exceptionally bright stars.
Naturally, our galaxy is not a stationary object in the vast expanse of the Universe. Presently, astronomers theorize that our galaxy, along with its neighboring galaxies (known as the Local Group of Galaxies), is a constituent of the supercluster of galaxies situated within the Virgo constellation. Investigations into relic radiation during the latter part of the 20th century revealed that the Solar System is in motion relative to relic radiation, with a velocity of 368 ± 2 km/s (equivalent to 78 astronomical units per year). As a result of this motion, an object located one million parsecs away and positioned perpendicularly to the extragalactic apex would demonstrate a proper motion of 78 angular microseconds per year (or millionths of an angular second) in the Earth’s sky. Recent decades have witnessed significant advancements in measurement accuracy, making such precise measurements well within reach. The measurement of proper motions in nearby galaxies relies heavily on imagery obtained from prominent ground-based telescopes, as well as space telescopes like Hubble and Gaia, along with data collected from radio interferometers. For instance, the calculation of the proper motion of the galaxy M31 has enabled astronomers to predict its eventual collision with our galaxy in a few billion years.
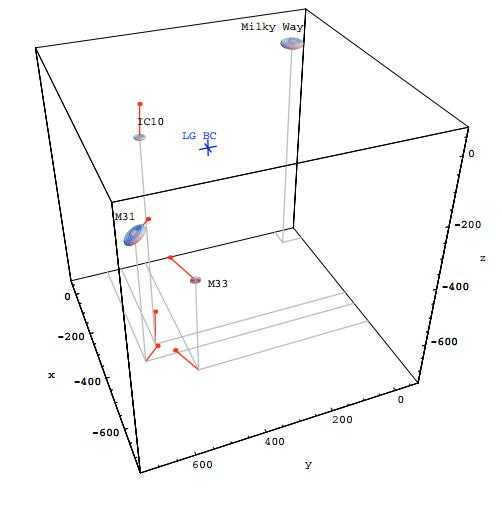

The diagram depicting the motion of galaxies within the Local Group in relation to our galaxy is based on the study conducted by A. Brunthaler et al. in 2007
The measured proper motion of the Andromeda galaxy at a distance of 0.8 million parsecs was approximately 50 angular microseconds per year. In contrast, modern radio interferometers have the capability to record galaxy proper motions based on maser observations up to a distance of 20 million parsecs over a period of 10 years. The challenge in measuring the proper motions of galaxies lies in the necessity to differentiate the overall motion of the entire galaxy from the orbital motion of individual star clusters or interstellar nebulae within it. The solution to this dilemma is to measure the proper motion of galaxy nuclei. In this regard, galaxies with active nuclei (quasars) – one of the brightest radio sources in the Earth’s sky – serve as a convenient source for measuring extragalactic proper motions. A paper published in 2005 titled “Quasar Apparent Proper Motion Observed by Geodetic VLBI Networks” reveals that geodetic radio interferometers were able to measure or limit the proper motion of 580 quasars between 1980 and 2002.
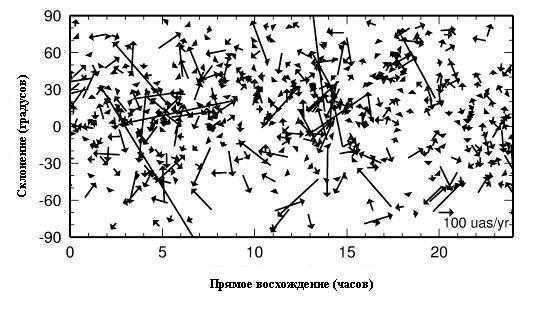
Several hundred angular microseconds are the proper motions of many of these celestial objects
The majority of these sources were situated at immense distances, spanning billions of light-years.
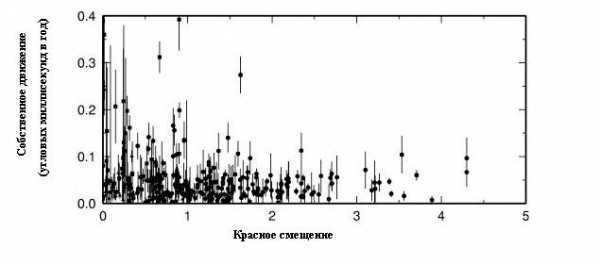
In 2017, a publication presented a comprehensive list detailing the proper motions of 713 extragalactic radio sources, which were observed over an average span of approximately 22 years. The measurements exhibited an average error rate of 24 angular microseconds per year. These observations enabled us to document the acceleration of the Solar System’s movement along its galactic orbit, with a statistical significance level of 6.3 sigma. This occurrence results in a systematic alteration in the angular velocity of extragalactic objects, amounting to several microseconds per year.
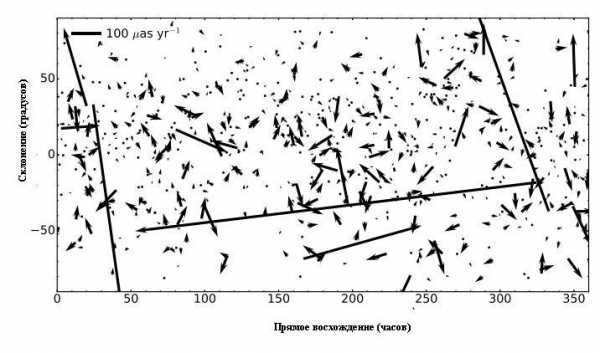
A map displaying the proper motions recorded in the recently released catalog is available for reference.
Among the entries in the catalog, the radio galaxy SDSS J213836.38+001241.8 stands out with the largest observed proper motion of approximately 1.5 angular milliseconds per year. This galaxy also boasts an observed optical luminosity of around 23 star magnitudes, with a redshift measurement of 0.6. For comparison, a neighboring galaxy, the Large Magellanic Cloud, exhibits a proper motion of 2 angular milliseconds.
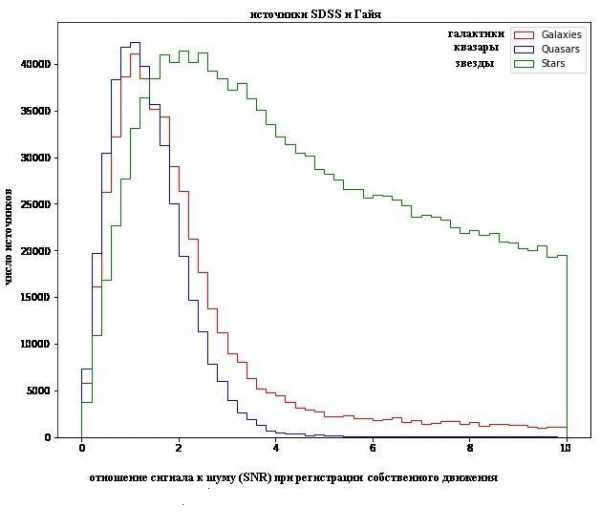

The initial publications of the GAIA space telescope, which functions in the optical spectrum, were also capable of detecting the proper movements of various galaxies and quasars.
In recent years, the importance of recording the proper motions of extragalactic objects has been growing due to the quest for dark matter. It has been hypothesized that dark matter exists based on the unusually high radial velocities observed in the outer regions of numerous galaxies. These radial velocities have been measured by analyzing the spectra. By measuring the proper motion of these anomalous regions, we can gain a better understanding of this phenomenon.
The lesser angle (at the celestial body) in a right-angled triangle where the hypotenuse represents the distance from the Sun to the celestial body and the smaller leg represents the major semi-axis of the Earth’s orbit. G. p. is utilized to calculate distances to celestial bodies: due to the immense distance of celestial bodies, their distances can be considered inversely proportional to G. p. Refer to Parallax (in astronomy).
Big Soviet Encyclopedia. – Moscow: Soviet Encyclopedia . 1969-1978 .
YEARLY PARALLAX refers to the angle at which a celestial luminary is observed in a right triangle. In this triangle, the hypotenuse represents the distance from the Sun to the luminary, while the shorter side represents the distance from the Sun to the Earth. Due to their small size, annual parallaxes can be considered inversely proportional … … … according to the Big Encyclopedic Dictionary
YEARLY PARALLAX – YEARLY PARALLAX is an angular displacement on the celestial sphere that occurs over a period of six months. This displacement occurs in a triangle where the opposite side of the angle is equal to half of the Earth’s orbit, which is equivalent to one astronomical unit … according to the Scientific and Technical Encyclopedic Dictionary
Yearly parallax refers to a small angle observed at a celestial object in a right triangle. In this triangle, the hypotenuse represents the distance (R) from the Sun to the celestial object, while the shorter cathetus represents the distance from the Sun to the Earth. Due to their small size, yearly parallaxes can be considered inversely proportional to R. This concept is often discussed in the Encyclopedic Dictionary of Natural Science.
PARALLAX – (ast.) The parallax is the angle formed by visual lines directed to the same object from two different points. Once the parallax of the object is known and the distance between the two points from which this object was observed, it is possible to determine the distance of the object from … … … The Dictionary of Foreign Words of the Russian Language
PARALLAX – (from Greek parallaxis deviation) 1) A parallax is an apparent change in the position of an object (body) due to the movement of the observer’s eye. 2) In astronomy, a parallax is an apparent change in the position of the celestial luminary due to the movement of the observer. There is a distinction between parallax, … … … The Big Encyclopedic Dictionary
PARALLAX – Parallax, parallax, man. (Greek. parallaxis evasion) (ast.). An angle that measures the apparent shift of a celestial body as the observer moves from one point in space to another. Daily parallax (the angle between the directions to the celestial body from a given location … Ushakov’s Explanatory Dictionary
Parallax – This term has other definitions, see Parallax. Parallax (meaning). Parallax diagram Parallax (Greek … Wikipedia
Parallax – a; m. [Greek parallaxis deviation] 1. Spec. The apparent shift of a observed object due to the movement of the observer’s eye. Correction for p. Error in calculations due to parallax. 2. Astron. The apparent shift of the celestial body (star relative … Encyclopedic Dictionary
The concept that stars are distant suns was first mentioned in ancient times. However, determining their exact distance from Earth remained a mystery for a long time. Aristotle himself realized that if the Earth was in motion, observing the position of a star from two opposite points on the Earth’s orbit would result in a change in the direction towards the star. This apparent displacement, known as parallax, could be used as a measure of the star’s distance: the greater the displacement, the closer the star. Surprisingly, neither Aristotle nor Copernicus were able to detect this displacement. It wasn’t until the late 19th century, when telescopes were equipped with precise angular measurement devices, that scientists were finally able to measure the parallax in the closest stars.
In 1837, the first reliable measurements of the annual parallax were taken. Russian astronomer Vasily Yakovlevich Struve (1793-1864) conducted these measurements for Vega (a Lyra), the brightest star in the Northern Hemisphere. Around the same time, scientists in other countries determined the parallaxes of two additional stars, one of which was Alpha Centauri. This particular star, which cannot be seen from Russia, turned out to be the closest to Earth. Its annual parallax was only 0.75″. To put this into perspective, a 1-mm-thick wire at this angle can be seen with the naked eye from a distance of 280 meters. It is no wonder that such minuscule angular displacements went unnoticed for so long.
The distance to the nearest star with a parallax of p = 0.75″ is calculated as D = 206265″/0.75″ = 270000 astronomical units. The units used to measure such vast distances are the parsec and the light year.
If accurate and meticulous measurements establish the annual parallax of a star, the distance D to the star can be determined using the formula: D = a/sinp, where a represents the radius of the Earth’s orbit. Considering the smallness of the angle p, which can be expressed in seconds of arc, we can rewrite the formula as: D = a/p”sinl.
If we take a as a unit, then, by knowing that sin1 = 1/206265, we can derive the formula: D = 206265/p”” astronomical units. Due to their vastness, distances to stars are usually expressed in light years or parsecs.
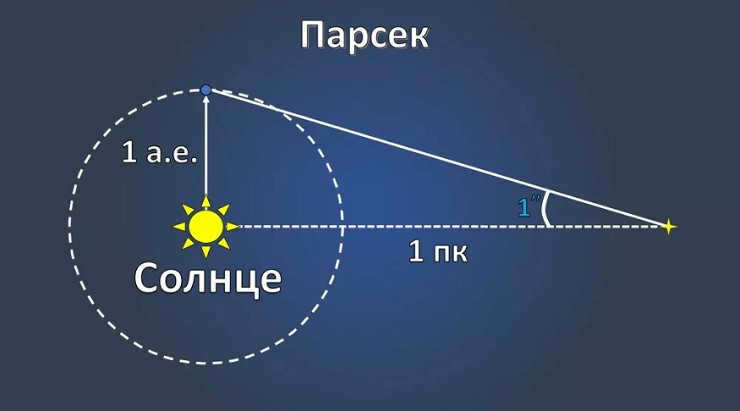
A light-year is the distance covered by a ray of light in the span of one year. To convert it into kilometers, one needs to multiply the speed of light by the number of seconds in a year. A parsec is a measurement of distance that corresponds to the annual parallax in one second of an arc. It represents the distance at which the line segment connecting the Earth and the Sun is observed at an angle of 1″.
The distance D to a star in parsecs can be calculated by taking the inverse of its annual parallax value p, expressed in seconds of an arc: D = 1/p”.
For instance, if the parallax of the closest star is 0″,75 (equivalent to 4/3 seconds of an arc), then its distance would be 4/3 parsecs.
1 parsec is equal to 3.26 light years, 206,265 astronomical units, or 3 x 10^13 kilometers.
The light emitted by the nearest and brightest star to us, Alpha Centauri, takes more than four years to reach us, and light from other stars takes even longer.
To grasp the vastness of this distance, let’s envision a jet aircraft traveling at a speed of 1000 km/h making its way from Earth to this particular star. It would take an astonishing 4.5 million years for the plane to reach its destination.
Other stars are even more remote from us (or, in other words, from the Sun). The distances to the majority of stars remain unknown – they are so immense that their parallaxes are too minuscule to be accurately measured using the aforementioned method. However, alternative methods of determining stellar distances have been developed based on the measurement of nearby star parallaxes.
The annual parallax of a star refers to the alteration in the star’s coordinates as a result of the observer’s change in position due to the earth’s orbit around the sun. This phenomenon provides evidence of the earth’s movement around the sun and serves as the primary means of determining distances to stars. The annual parallax value of a particular star corresponds to the angle at which the major semi-axis of the Earth’s orbit is perceived from the star’s location. Due to the vast distances to stars, even the closest ones exhibit annual parallaxes that are less than a fraction of a second of arc.
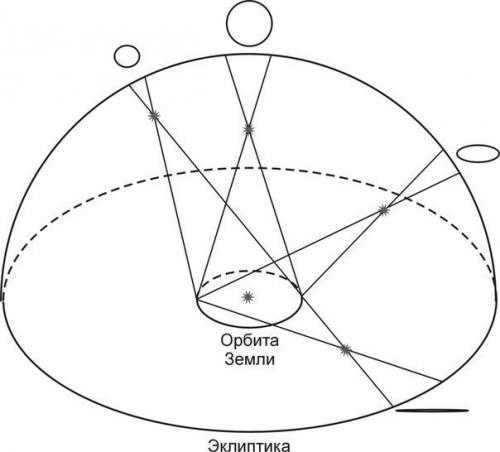
Primary positions.
Due to the earth’s orbit around the sun, the positions of stars in the sky must undergo a parallactic shift. The visible path of a star’s trajectory in the sky takes the shape of an ellipse, with the major semi-axis being parallel to the ecliptic.
If the star is observed close to the ecliptic, the maximum parallactic angle, which is the angle formed by the star, the earth, and the sun, can be determined using the following equation.
sin p = a/r, where a represents the distance between the earth and the sun, and r is the distance from the sun to the star. Only when the star is observed near the pole of the ecliptic, the parallactic angle is calculated using the formula.
p=1/r (1? 1/206 265 radians, 1 pc? 206,265 a. e. . So, when the parallax is 1", the distance to the star is equivalent to one parsec.
When measuring stellar parallaxes, it is common practice to determine the star’s position relative to other, much fainter stars, which are assumed to be significantly farther away than the star being studied (differential method of measuring annual parallaxes).
In addition to the annual parallax, there are currently other methods for determining the distance to stars. However, all of these methods ultimately require calibration using the parallactic method.
How is parallax measured?
The measurement of parallax is determined by the angle at which the major semi-axis of the Earth’s orbit (perpendicular to the line of sight) is observed from a star. The distance to an object with an annual parallax of 1 arc second is referred to as a parsec (1 parsec = 3.085678-1016 meters).
What does parallax mean in astronomy?
Parallax, also known as parallactic displacement, is a phenomenon in astronomy that refers to the apparent movement of celestial objects on the celestial sphere. This movement is caused by the observer’s motion in space due to the rotation of the Earth (known as diurnal parallax), the Earth’s revolution around the Sun (known as annual parallax), and the movement of the solar system within the Galaxy (known as secular parallax).
Galaxy. Galaxies
Galaxies are vast formations of stars, gas, and dust that are bound together by the force of gravity. These immense structures in the universe can vary in shape and size. Most celestial objects are part of a specific galaxy. These include stars, planets, satellites, nebulae, black holes, and asteroids. Some galaxies contain substantial amounts of invisible dark energy. Because galaxies are separated by empty space, they are often referred to as oases in the cosmic desert. On the Kvant.Space space portal, you can find articles about galaxies and their constituents.
Tabular overview of the main types of galaxies
| Spheroidal component | The entire galaxy | Yes | Very faint |
| Stellar disk | None or weak | Main component | Main component |
| Gas-dust disk | No | Yes | Yes |
| Spiral branches | No or only near the core | Yes | No |
| Active nuclei | Present | Present | No |
| Percentage of total number of galaxies | 20% | 55% | 5% |

Our Milky Way
The Milky Way galaxy contains billions of stars, including our closest star, the Sun. When we gaze at the night sky, we are greeted by a vast array of stars. This celestial spectacle was referred to as the Galaxy by the ancient Greeks.

If we had the chance to observe this star system from an external perspective, we would witness a flattened sphere containing over 150 billion stars. The enormity of our galaxy is difficult to fathom. It would take a beam of light a hundred thousand Earth years to travel from one side to the other! The center of our Galaxy is occupied by the nucleus, which gives rise to massive spiral arms teeming with stars. The distance from the Sun to the core of the Galaxy spans 30,000 light years. The solar system resides on the outskirts of the Milky Way.
Despite the vast collection of cosmic bodies, stars within the Galaxy are scarce. To put it into perspective, the distance between the closest stars is tens of millions of times larger than their diameters. It would be incorrect to assume that stars are randomly scattered throughout the Universe. Their placement is influenced by gravitational forces, which keep these celestial bodies within a specific plane. These star systems, with their own gravitational fields, are referred to as galaxies. In addition to stars, galaxies consist of gas and interstellar dust.
There are numerous other galaxies that constitute the entirety of the Universe. The ones closest to us are situated approximately 150,000 light-years from our location. These galaxies can be observed in the southern hemisphere’s sky in the form of tiny, hazy patches. They were initially documented by Pigafett, who was part of the Magellanic expedition that circumnavigated the globe. These celestial formations are scientifically referred to as the Large and Small Magellanic Clouds.

The Andromeda Nebula, also known as the closest galaxy to us, can be easily observed from Earth using regular binoculars. In fact, on a clear day, it can even be seen with the naked eye due to its significant size.

The galaxy has a remarkable shape that can be described as a colossal spiral curve in the vastness of space. Positioned on one of the spiral arms, at a distance of about three-quarters from the center, lies our solar system. Every celestial object within the galaxy orbits around the central core, influenced by the immense gravitational force it exerts. Back in 1962, astronomer Edwin Hubble categorized galaxies based on their appearance, resulting in the classification of elliptical, spiral, irregular, and junction galaxies.

There are countless galaxies in the portion of the Universe that is accessible to astronomical research. Astronomers collectively refer to them as the Metagalaxy.
The galaxies of the Universe
Galaxies are vast collections of stars, gas, and dust that are held together by gravity. They can vary greatly in shape and size. The majority of cosmic objects belong to a galaxy, including black holes, asteroids, stars with satellites and planets, nebulae, and neutron satellites.

Annual Parallax Video. Part 1: explanation
History of Horizontal Parallax
The geocentric parallax, commonly known as the diurnal parallax, refers to the angle at which the Earth’s radius is observed from a specific celestial body. Another important concept to consider is the horizontal parallax. The horizontal parallax is the angle at which the equatorial radius of the Earth is observed from the center of a celestial body when it is positioned on the true horizon. The true horizon is a theoretical circle on the celestial sphere that is perpendicular to the plumb line at the observation point. The distinction between diurnal and horizontal parallax arises from the Earth’s non-spherical shape, with the polar radius being 21 km shorter than the equatorial radius.
The parallax of the Moon and Sun was first determined by ancient Greek astronomers through observations of lunar eclipses. This allowed them to calculate the parallax of the Moon from a fixed location. Hipparchus of Nicaea (180-125 BC), an ancient Greek astronomer, estimated the parallax of the Sun to be 7 angular minutes in 129 BC, which is the maximum angle that can be detected by the naked eye. Prior to Hipparchus, Aristarchus of Samos (310-230 BC) also made similar calculations.
However, Claudius Ptolemy, an astronomer from Alexandria (100-170 AD), had a different belief regarding the distance to the Moon. He thought that it varied depending on its phases. This created a significant disagreement among the ancient astronomers when it came to estimating the parallaxes of the Moon and the Sun. Ptolemy’s error in assuming that the size of the Moon’s parallax was connected to its phases later became one of the main criticisms of the Ptolemaic world system. It was during his time in Italy that a young Nicolaus Copernicus (1473-1543 AD) measured the Moon’s parallax with his teacher Novara. Their observations during the eclipse of the bright star Aldebaran in Bologna on March 9, 1497 revealed that the Moon’s parallax was not influenced by its phase. As centuries passed, simultaneous observations from both the northern and southern hemispheres became common practice in accurately measuring the parallaxes of the Moon, Sun, and Mars. For instance, in the 18th century, such observations were conducted at the Cape of Good Hope Observatory in southern Africa and the Berlin Observatory.
Parsec. What does the term “parsec” mean?

Definition of the term
What does parsec mean?
Luminosity
Luminosity refers to several physical quantities.
In the field of photometry, luminosity is a measure of the light flux emitted from a small area of a luminous surface per unit area. It is calculated by dividing the luminous flux emitted from the specific area of the surface by the area itself:
where dΦv is the luminous flux emitted from a surface area of d S. Luminosity in the International System of Units (SI) is measured in lm/m². 1 lm/m² corresponds to the luminosity of a surface with an area of 1 m2 that emits a light flux of 1 lm.
The energy photometric quantity that corresponds to luminosity is energy luminosity (emissivity). Its definition is similar to that of luminosity, but it uses radiation flux Fe instead of light flux Φv. The SI unit of energy luminosity is W/m².
In astronomy, luminosity refers to the total energy emitted by an astronomical object (such as a planet, star, or galaxy) per unit time. It is typically measured in absolute units (SI – W; GHS – erg/s) or in units relative to the Sun’s luminosity (L ☉ = 3.86⋅1033 erg/s = 3.86⋅1026W).
The luminosity of the brightest stars is millions of times greater than that of the Sun.
In the field of experimental particle physics, luminosity serves as the indicator of the intensity of particle collisions between beam particles and particles of a stationary target (or between particles of two opposing beams in the case of colliders). Luminosity, denoted as L, is quantified in units of cm-2-s-1. The product of the reaction cross section and the luminosity provides the average rate of this process within a specific collider, denoted as N˙process=L⋅σprocess>_>=L\cdot \sigma _>> .
The initial luminosity of the Large Hadron Collider during the early stages of operation was limited to 1029 particles/cm²-s. However, it has been steadily increasing since then. The ultimate objective is to achieve a nominal luminosity of 1.7⋅1034 particles/cm²-s, which is comparable to the luminosity levels observed at the BaBar facility in SLAC, USA, and the Belle facility in KEK, Japan. Notably, the KEKB collider currently holds the world record for luminosity in gas pedal systems with counter beams, with a value of 2.11⋅1034cm-2-s-1.
How can we determine the distance to a star using parallax?
To calculate the distance D to a star in parsecs, we can use the inverse of its annual parallax p, which is measured in seconds of arc. For instance, if the closest star has a parallax of 0.75 (or 4/3) seconds of arc, its distance would be 4/3 parsecs. It’s important to note that 1 parsec is equivalent to 3.26 light-years, 206,265 astronomical units, or 3*10^13 km.
The annual parallax of a star is a phenomenon that occurs when the observer’s position changes due to the Earth orbiting around the Sun. This change in position causes a shift in the star’s coordinates and serves as evidence for the Earth’s motion around the Sun. It is also the primary method used to measure distances to stars. The annual parallax of a specific star can be calculated by determining the angle at which the major semi-axis of the Earth’s orbit is visible from the star’s location. Due to the vast distances to stars, even the closest ones have annual parallaxes that are less than one second of arc.
The stellar parallax serves as the foundation for the parsec, which is a unit of distance used in astronomy. The parsec represents the distance from the Sun to an astronomical object that has a parallax angle equal to one arc second. It is important to note that the scale of 1 a.u. (astronomical unit) and 1 parsec are not proportional, with 1 parsec being approximately equal to 206,265 a.u.
Stellar parallax refers to the apparent movement of a nearby star (or any other object) against the backdrop of far-off objects. This phenomenon is caused by the varying positions of the Earth as it orbits the Sun. The observed shift is most pronounced when the Earth is on opposite sides of the Sun, which happens approximately every six months. During this time, the distance between observations is about two astronomical units. The parallax itself is regarded as half of this maximum shift, which is roughly equivalent to the observed movement that would result from the different positions of the Earth and the Sun, with a baseline distance of one astronomical unit (Australia).
The detection of stellar parallax has posed a significant challenge in the field of astronomy for centuries, leading to numerous debates. However, in 1838, Friedrich Bessel successfully measured the parallax of the star 61 Swan using the Fraunhofer heliometer at the Königsberg Observatory.
Throughout the course of one year, the relative position of the star S is observed in relation to other stars that are visible in its vicinity:
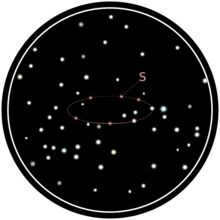

Reference points are used to determine the path of S, which are stars that did not show any apparent movement relative to each other.
The path observed is in the form of an ellipse, which is a projection of the Earth’s orbit around the Sun. This projection is made against a distant backdrop of fixed stars, with the point S representing the Earth’s position. As S moves further away from the Earth’s orbital axis, the eccentricity of its path increases. The center of the ellipse corresponds to the point where S is visible from the Sun:
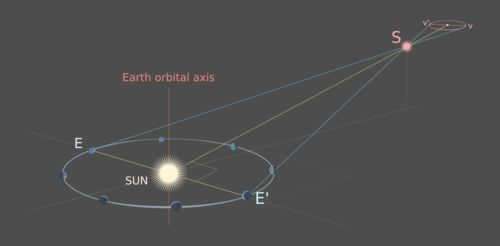
In astronomy, stellar parallax refers to the apparent shift in the position of a star when observed from different points in Earth’s orbit around the Sun. This shift occurs because the plane of Earth’s orbit is at an angle to the line from the Sun through the star. The vertices v and v’ represent the Earth’s positions E and E’ projected onto the elliptical path of the star S. The line E-E’ intersects the line Sun-S at a right angle point, creating an isosceles triangle with the points E, E’, and S. The line Sun-S serves as the axis of symmetry for this triangle.
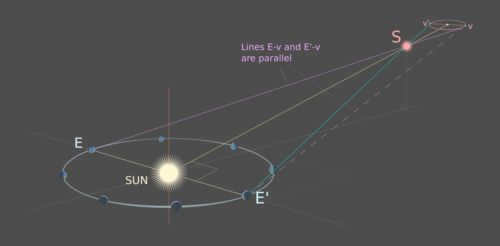
Given that the line E’-v’ intersects the parallel lines Ev and E’-v in the same (approximately Euclidean) plane, it can be concluded that the angles at which these parallel lines intersect with the transversal are identical. In other words, the angle θ formed by the rays of sight of Ev and E’-v’ is equal to the angle θ formed by E’-v and E’-v’, which represents the angle θ between the observed positions of S relative to its seemingly stationary stellar surroundings.

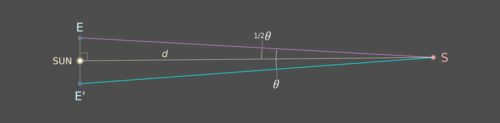
The current distance from the Sun to S can be determined using basic trigonometry:
Therefore, the distance, d, can be calculated as E-Sun divided by the tangent of half the angle, θ, where E-Sun is equal to 1 AU.
Parallax decreases as the distance between the observer and an object increases.
Measurements of stellar parallax are given in small units of angular seconds or even milliseconds. The distance unit parsec is defined as the length of a segment of a leg of a right triangle, adjacent at an angle of one angular second at one vertex, where the length of the other leg is 1 AU. Because stellar parallaxes and distances involve such thin right-angled triangles, a convenient trigonometric approximation can be used to convert parallaxes (in arc seconds) to distance (in parsecs). The approximate distance is simply the inverse of the parallax: d (pc) ≈ 1 / p (arcsec). > \ approximately 1 / p >.> For instance, Proxima Centauri (the closest star to Earth other than the Sun), with a parallax of 0.7685, is at a distance of 1 / 0.7685 parsecs = 1.301 parsecs (4.24 sv years).

Dollond’s heliometer from the end of the 1700s
The concept of stellar parallax was not observable until the 19th century, making it a scientific argument against the heliocentric model during the early Modern Age. Based on Euclid’s geometry, it was understood that the effect would be too small to detect if the stars were located far enough away. However, due to various factors, such vast distances seemed unlikely. This was one of Tycho Brahe’s primary objections to Copernicus’ heliocentric model, as it required a massive and improbable gap between the orbits of Saturn and the eighth sphere (fixed stars) to explain the absence of observable stellar parallax.
James Bradley made his first attempt to measure stellar parallaxes in 1729. However, the telescope he used was unable to detect the motion of the star. Instead, he discovered aberrations of light and nutations of the Earth’s axis. During this endeavor, he was able to catalog 3,222 stars.
The 19th and 20th centuries
 Bessel heliometer
Bessel heliometer  Bamberg heliometer split lens (late nineteenth century)
Bamberg heliometer split lens (late nineteenth century)
One common method for measuring stellar parallax is through the use of annual parallax. This is determined by observing the difference in position of a star when viewed from both the Earth and the Sun. In other words, it measures the angle at which the star appears to move against the background of the Earth’s orbit around the Sun. The distance measurement unit used for annual parallax is the parsec, which is equivalent to 3.26 light-years. A parsec is defined as the distance at which the annual parallax of a star is equal to 1 arc second.
To measure annual parallax, astronomers observe the position of a star at multiple points throughout the year as the Earth orbits around it. This allows them to calculate the change in the star’s apparent position due to the Earth’s motion. Measuring annual parallax was a significant breakthrough in determining distances to nearby stars, as it provided the first reliable method for such calculations. The first successful measurements of stellar parallax using this method were conducted by Friedrich Bessel in 1838. He used a heliometer, a specialized instrument for measuring small angles, to observe the star 61 Swan.
Due to its challenging measurement, the number of stellar stars is estimated to be only around 60. By the end of the 19th century, parallaxes were obtained using the thread micrometer, resulting in limited data. However, the early 20th century saw a significant advancement with the introduction of astrographs and astronomical photographic plates, which accelerated the process. The 1960s brought about further progress with the introduction of automated plate measuring machines and advanced computer technology, allowing for more efficient compilation of star catalogs. Finally, in the 1980s, charge-coupled devices (CCDs) replaced photographic plates, reducing the optical error to just one millisecond of arc.
Stellar parallax remains the prevailing method for calibrating other measurement techniques (see Cosmic distance ladder). Accurate distance calculations based on stellar parallax necessitate determining the Earth-Sun distance, which is currently known with remarkable precision utilizing radar reflections from planetary surfaces.
The angles involved in these calculations are exceedingly small and therefore pose a challenge for measurement. The nearest star to the Sun (and also the star with the greatest parallax), Proxima Centauri, exhibits a parallax of 0.7685 ± 0.0002 arc second. This angle is roughly equivalent to the angle formed by a 2 centimeter diameter object at a distance of 5.3 km.
In 1896, the Kaffner Observatory in Vienna acquired a spacious heliometer, which was employed for the purpose of measuring the distances to various stars through trigonometric parallax. By the year 1910, this remarkable instrument had successfully deduced the parallax distances of 16 stars, out of the 108 celestial bodies that were already acknowledged by the scientific community during that era.
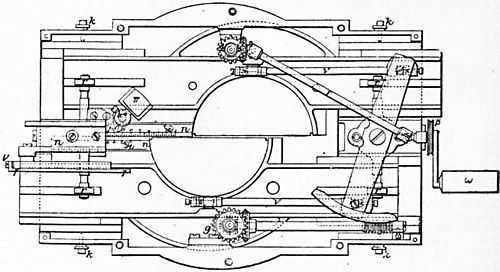
The 1911 Encyclopedia Britannica included a diagram of a divided heliometer lens, designed to serve as a visual representation of a heliometer.
Utilizing cosmic astrometry to calculate parallax
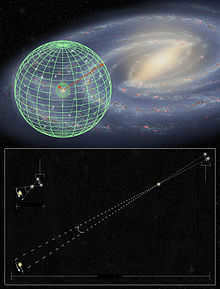
The Hubble telescope has significantly expanded its ability to accurately measure the distance to stars, now reaching 10 times farther into the Milky Way galaxy.
In 1989, the launch of the Hipparcos satellite revolutionized the field of astronomy by greatly increasing the number of stellar parallaxes measured with extreme precision. By a factor of a thousand, Hipparcos surpassed previous capabilities, allowing for millisecond accuracy in parallax angles. However, its range was ultimately limited to stars within a distance of about 1,600 light-years, just over one percent of the Milky Way’s vast diameter.
The accuracy of the Hubble telescope’s WFC3 has now reached 20 to 40 microseconds, enabling it to accurately calculate distances of up to 3,066 parsecs (10,000 light-years) for a select few stars. This advancement greatly improves the precision of the cosmic distance ladder and enhances our understanding of distances in the universe based on Earth’s orbit.
The Gaia mission, launched by the European Space Agency on December 19, 2013, is projected to measure parallax angles with a precision of 10 micro angular seconds for moderately bright stars. This means that it can map nearby stars (and potentially planets) that are tens of thousands of light-years away from Earth. The 2018 Data Release 2 indicates that the average errors for parallax measurements of stars with a magnitude of 15 or brighter are 20-40 microseconds.
Using Radio Astrometry for Parallax Measurements
Radio interferometry, with its ability to produce high-resolution images, offers a unique advantage in accurately measuring parallax. In fact, the angular resolution achieved through this method can be as precise as 1 millisecond, surpassing the capabilities of optical telescopes like Gaia. While radio measurements have limited sensitivity and require individual observations, they are particularly effective for studying sources such as pulsars and X-ray double systems, where radio emission is significantly stronger than optical emission.
Statistical parallax
There are two methods that are used to estimate the average distances to stars by studying the motion of stars. These methods are known as statistical parallaxes, or individually as century parallaxes and classical statistical parallaxes.
The movement of the Sun in space creates a longer baseline, increasing the precision of parallax measurements called century parallax. In the Milky Way disk, this results in an average baseline of 4 a.u. per year for stars, while halo stars have a baseline of 40 a.u. per year. In the coming decades, the baseline could be significantly larger than the traditional Earth-Sun baseline used for parallax. However, century parallax introduces more uncertainty due to the additional unknown of the relative velocity of other stars. By studying a small sample of stars, the uncertainty can be reduced, and accuracy is inversely proportional to the square root of the sample size.
The estimation of mean parallaxes and distances for a significant cluster of stars can be achieved by considering their radial velocities and proper motions. This approach is commonly referred to as classical statistical parallax. The movement of stars is mathematically represented to statistically recreate the velocity dispersion in relation to their distances.
Alternative application of parallax in astronomy
There are other applications of the term parallax in astronomy that do not involve actual parallax measurements. These include the photometric parallax method, spectral parallax, and dynamic parallax.