
At present, 58,745 educational institutions are eligible for additional cumulative discounts ranging from 2% to 25%. To determine the applicable discount for all staff members at your educational institution, please log in to your personal Infoworks account.


Enrichment program for professional growth
Engaging in Sports Orienteering as an Instructor-Methodologist
We can include your educational institution’s discount along with this offer (the amount will depend on the number of your colleagues who have completed Infoworks courses).
Currently, a total of 58,745 educational institutions benefit from additional discounts ranging from 2% to 25%. To determine the discount available for all staff members at your educational institution, please log in to your personal Infoworks account.


Professional retraining course
Law: theory and methodology of teaching in an educational organization
We have the ability to incorporate your school’s discount with this offer (the amount will vary based on the number of your colleagues who have enrolled in Infoworks courses).
At present, 58,745 educational institutions are eligible for additional discounts ranging from 2% to 25%. To determine the discount available to all staff members at your school, please log in to your personal Infoworks account.


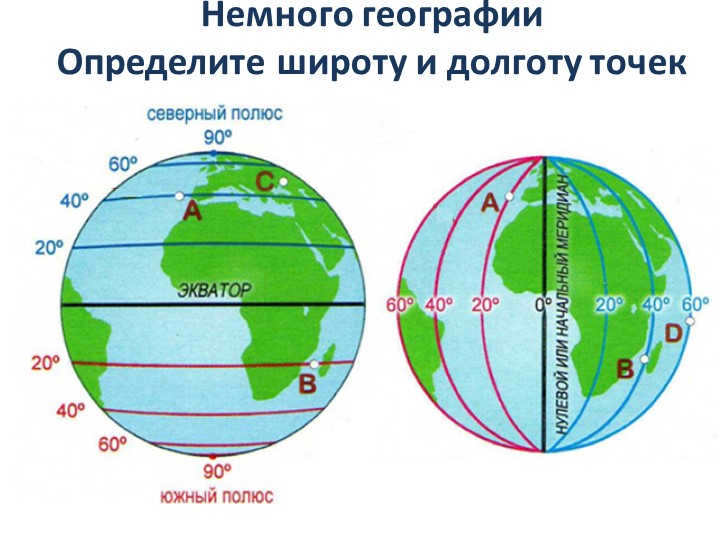
A portrayal of a contemporary learner within an academic setting
Breakdown of the presentation content in distinct slides:

Slide 2 Lesson Goals
Understanding and describing the transformation in the appearance of the nighttime sky throughout the day
Having the capability to resolve questions concerning the geographical latitude, culmination, and elevation of a celestial body.

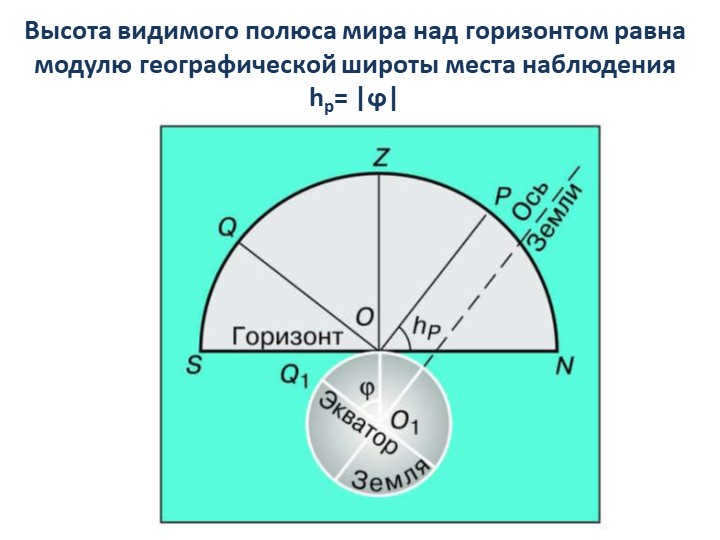
According to slide 7, the visible pole of the world above the horizon has a height equal to the modulus of the geographic latitude of the place of observation, hp = ϕ.
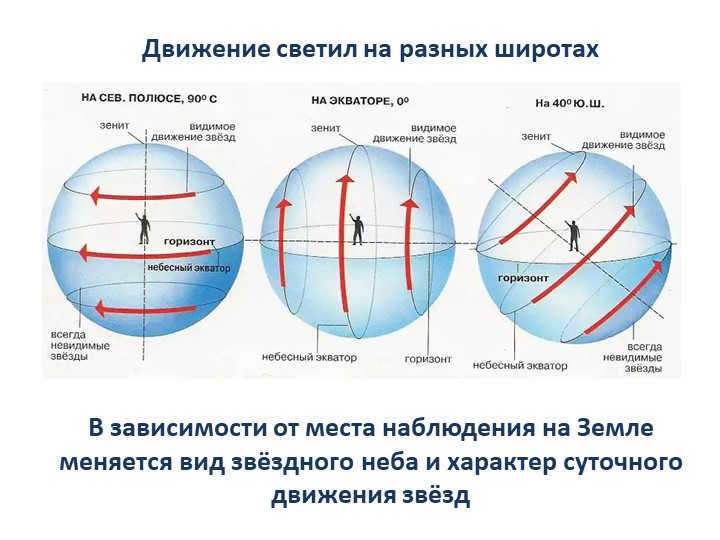
Slide 8: The starry sky and the daily motion of the stars vary depending on the observer’s location on Earth. The movement of celestial bodies differs at different latitudes.
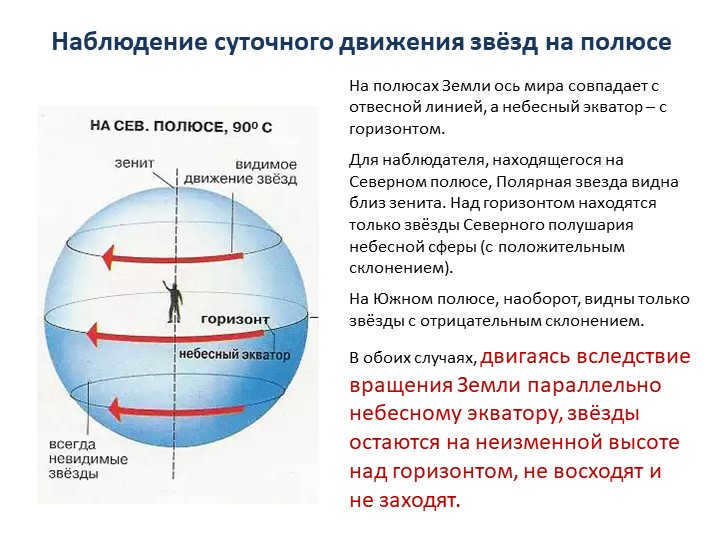
Slide 9: The act of observing the daily movement of the stars at the pole
When located at the Earth’s poles, the axis of the world aligns with the plumb line, while the celestial equator aligns with the horizon.
For an individual situated at the North Pole, Polaris becomes visible near the zenith. Only the stars of the northern hemisphere of the celestial sphere (with positive declination) can be seen above the horizon.
On the other hand, at the South Pole, only stars with negative declination are visible.
When the Earth rotates parallel to the celestial equator, the stars stay at the same height above the horizon without rising or setting, regardless of the situation.
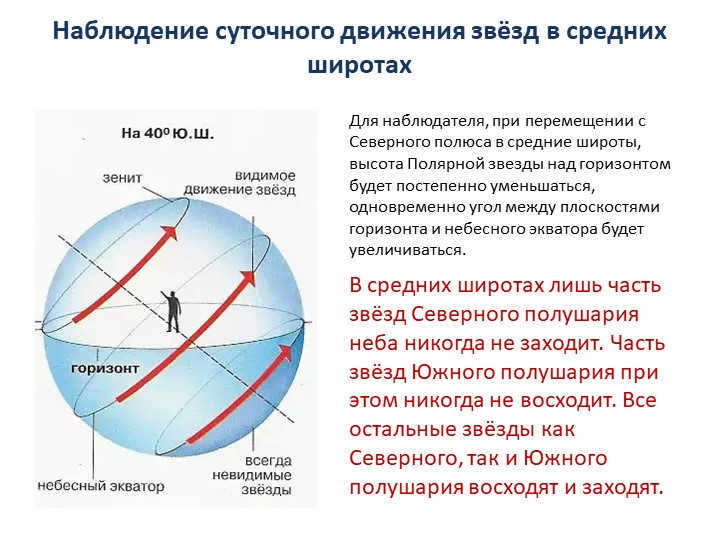
When an observer moves from the North Pole to the middle latitudes, they will notice a gradual decrease in the altitude of Polaris above the horizon. Simultaneously, the angle between the planes of the horizon and the celestial equator will increase.
In the middle latitudes, only a portion of the stars in the Northern hemisphere never set. Conversely, some stars in the Southern Hemisphere never rise. However, all other stars in both the Northern and Southern Hemispheres rise and set.
When observing the daily motion of stars in the middle latitudes, it is important to note that…
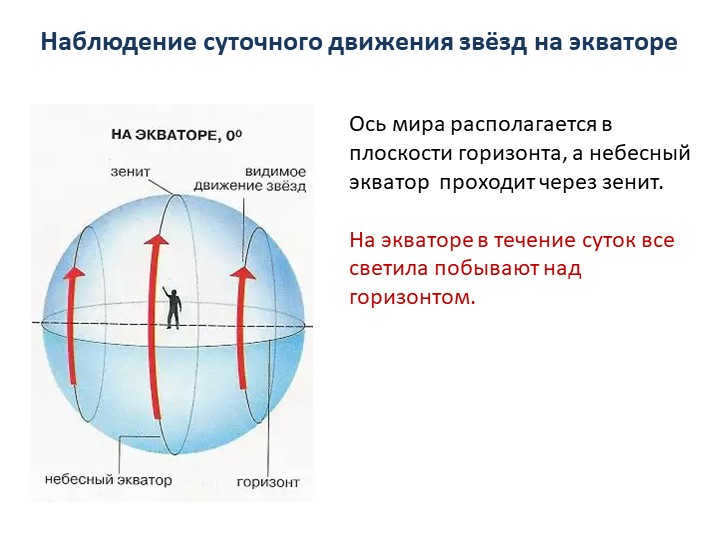

Slide 11: The axis of the world is situated on the plane of the horizon, and the celestial equator intersects it at the zenith.
At the equator, all celestial bodies will be above the horizon throughout the day. When observing the daily movement of stars at the equator, one can notice…

13 slide The upper and lower culmination of a celestial body at δHorizon
Celestial equator
Polaris
ϕ – geographic latitude
δ – declination of the celestial body
During its daily motion, celestial bodies cross the celestial meridian twice.
The moment when a celestial body crosses the celestial meridian is known as culmination.
At the moment of upper culmination, the celestial body reaches its highest point above the horizon.
Pole of the world
hmax = 90° – ϕ + δ
The case when δ = ϕ
hmax = 90°
hmin = 2ϕ – 90°
Upper – on the Z side of the world axis
Lower – on the Z’ side of the world axis
at δhmin = -(90° – ϕ) + δ
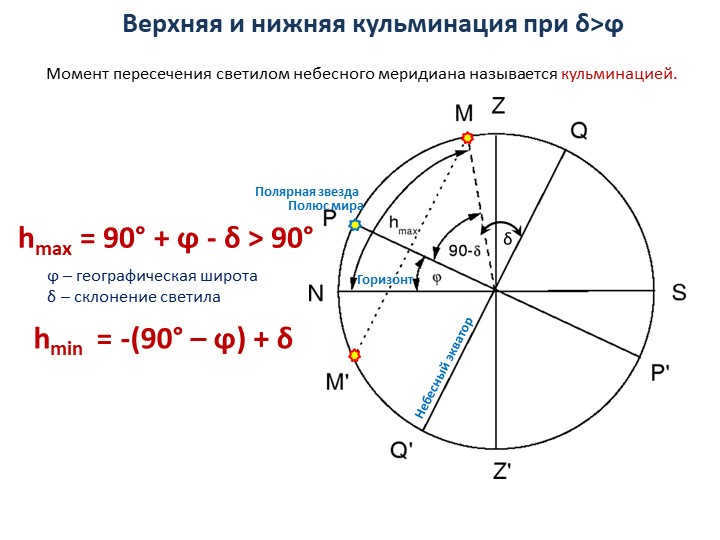
At δ>ϕ, the upper and lower culmination occur. The upper culmination refers to the moment when the luminary crosses the celestial meridian, while the lower culmination is the opposite. The luminary can be Polaris or any other celestial object. The geographic latitude is denoted by ϕ, and the declination of the luminary is represented by δ. The celestial equator and the pole of the world are also important concepts in this context. The maximum altitude of the luminary during the upper culmination is calculated using the formula hmax = 90° + ϕ – δ, and it is always greater than 90°. On the other hand, the minimum altitude during the lower culmination is given by hmin = -(90° – ϕ) + δ.


In slide 15, Sirius (α B. Psa, see Appendix IV) was at its highest point in the sky, with an altitude of 10 degrees. What is the latitude of the observation location?
Here is an example of how to solve the problem:
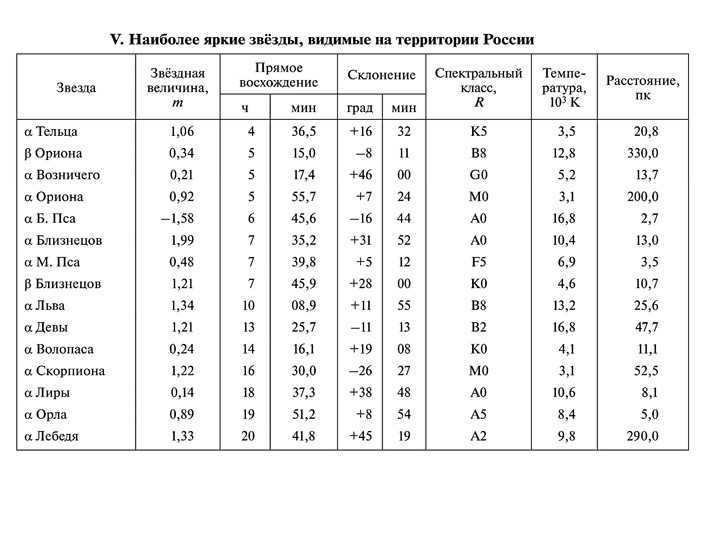
The observation site’s latitude can be determined by analyzing the position of Sirius (α B. Psa, see Appendix IV) at its upper culmination, which was at an altitude of 10°.
To find the latitude, we can use the example of problem solution.


During the 18th slide, Sirius (α B. Psa, see Appendix IV) was at its highest point in the sky with an elevation of 10 degrees. What is the latitude of the observation location?
Here is an example of how to solve the problem.
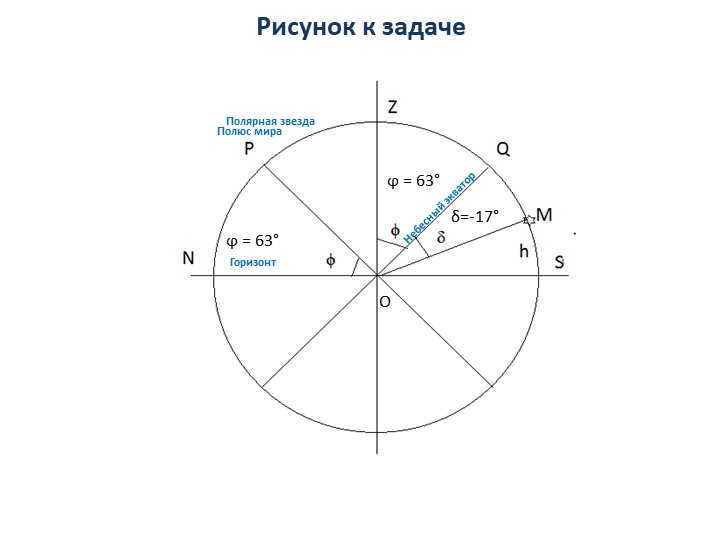
There are 19 slides available to solve the problem.
ϕ is equal to 63 degrees.
ϕ is also equal to 63 degrees.
δ is equal to -17 degrees.
The celestial equator is an important concept to understand. The horizon is another key term. Polaris is a significant celestial object. The world pole is a crucial point to consider. О is an additional element to take into account.


20 slide Questions
What evidence can you gather from observing the starry sky and its rotation to conclude that the observer is located at the North Pole of the Earth?

21 slide Questions
Which location on the Earth does not have any visible stars in the northern sky?
At the North Pole, no stars from the southern celestial hemisphere can be seen, and at the South Pole, no stars from the northern celestial hemisphere can be seen, respectively.

Slide 22 Exercise (on your own)
Number 1. Kiev is located at a geographic latitude of 50 degrees. What is the altitude in this city where the star Antares reaches its upper culmination, with a declination of -26 degrees?
Create an appropriate illustration.

23 slide Exercise 4 (p. 31)
№1. The latitude of Kiev is 50°. What is the altitude in this city where the star Antares reaches its highest point, with a declination of -26°?
Create a corresponding diagram.
Construct a diagram, considering that
the height of the North Star above the horizon
is equal to the latitude:
hp=ϕ, ϕ=50°, hp=50°
NOP=ZOQ
The star’s declination is negative, indicating that it is located south of the celestial equator.
2) Determine the altitude of the highest point of the star
h = 90° – ϕ + δ
h = 90°- 50°- 26°=14°
ϕ = 50°
ϕ = 50°
δ=-26°
Celestial equator
Horizon
Polaris
North Star
О

Resources and materials for teachers and educators
More than 10,000 educational materials for school and home learning
At the highest point of Altair, a star, its altitude was 12 plus the declination of the star, which was 9. What is the geographical latitude of the observation location? Please provide a necessary diagram.

The science that studies celestial bodies is known as astronomy. It is a branch of science that deals with the observation and study of stars, planets, galaxies, and other celestial objects. Astronomers use various tools, such as telescopes and satellites, to gather data and analyze celestial phenomena. They also study the physical and chemical properties of celestial bodies and their interactions with each other. Astronomy plays a crucial role in our understanding of the universe and has contributed to numerous scientific advancements.
H = 90 degrees – F(phi) + delta

What actions should be taken in public areas?
What actions should be taken in public areas.
Elucidate the necessity for implementing the fresh European style of attire?
Elucidate the necessity for implementing the fresh European style of attire.

Need immediate assistance?
I have a pressing task at hand which consists of 26 different variations. These tasks need to be completed using a compass. Are there any existing projects or drawings that can be utilized for this purpose?

Which observations are necessary to detect the moon’s motion?
Which observations are required to detect the movement of the moon?

Is it Astronomy, 11th grade?
The latitude of Kiev is 50°.
What is the height above the city where the star Antares, with a declination of -26°, reaches its highest point?
Create a suitable illustration.
An illustration is what we really need.
The sun is at an altitude of 30° at noon and its declination is – 19°.
Find out the geographical latitude of the observation location.

Which geographic latitude experiences the sun directly overhead at noon on March 21 and June 22?
Which latitude on Earth has the sun directly above it at noon on March 21 and June 22?

What is the elevation of the Peace Pole at the latitude of Moscow (55° 45′ s?
What is the height of the Pole of the World at the latitude of Moscow (55° 45′ s. What is the altitude of the World Pole at the latitude of Moscow (55° 45′ s.?

What is the altitude of the North Pole on Earth where the center of the sun is exactly on the horizon on June 22?
What is the height of the Earth’s North Pole at the location where the center of the sun is exactly on the horizon on June 22?
Discover how leg muscles function.
Find out how leg muscles work.
On this page, you will discover the solution to the following query: What is the geographic latitude of the observation site if the altitude of the star Altair at its highest point was 12 degrees plus its declination of 9 degrees? This question falls under the category of Other subjects and is suitable for students in grades 10 – 11. In case the answer doesn’t fully address your search, you can find additional responses from other users below or engage in a discussion on the relevant topic. Utilize the Smart Search feature to explore similar questions within this category. If none of the suggested answers match your requirements, you can try reformulating the question yourself by using the button located at the top of the page.

Cleomedes is credited with this assertion regarding the scientific study of celestial bodies.

Matrimony – within the realm of familial legislation, a consensual and egalitarian partnership between a female and a male, entered into with the intention of establishing a family unit and forging reciprocal rights and responsibilities between the married individuals, is formalized through the process of marriage registration. AFFECTION – a profoundly affirmative sentiment….
Uryupinsk. The Goat Museum. Operational since 2003.

Provide detailed information about your school, such as its location, the language of instruction, the courses offered, the activities students engage in during their free time, and any additional features.

It is important to avoid bringing electronic devices to school, as they can pose a fire or electric shock hazard. Using electronic devices in school may lead to device malfunction or damage, and can also put students at risk of fire or electric shock. Please refrain from bringing electronic devices to school. Thank you.

The study of celestial bodies is known as astronomy. Mankind has always been fascinated by the unknown and mysterious nature of space. Outer space is the vast expanse that exists between celestial bodies. The atmospheres surrounding stars and planets extend indefinitely, gradually thinning out as the distance from the celestial body increases. Beyond a certain altitude, this thinning atmosphere marks the beginning of space. In this article, we will explore the temperature of space and other intriguing facts about the cosmos….
In the vast expanse of outer space, a high vacuum prevails, characterized by a low density of particles. It is a realm devoid of air, yet far from empty. Rather, space is composed of a variety of constituents:
- Gases,
- Cosmic dust,
- Elementary particles such as neutrinos and cosmic rays,
- Electric, magnetic, and gravitational fields,
- And electromagnetic waves, specifically photons.
Within the domain of an absolute or near-absolute vacuum, space becomes transparent, enabling us to behold the awe-inspiring beauty of distant celestial bodies, including galaxies. However, the presence of interstellar matter can also cast a haze, posing challenges to our observations.
It is important to note that the concept of space should not be conflated with the universe, a vast realm encompassing all celestial entities, including stars and planets.
The act of traversing or journeying through outer space is commonly referred to as space travel.
The starting point of the universe

The specific altitude at which outer space commences is indeterminate. The Karman Line, defined by the International Aviation Federation, designates the boundary of space at 100 kilometers above sea level.
In order for an aircraft to attain lift, it must reach the minimum velocity required for space travel. The U.S. Air Force has identified an altitude of 50 miles (approximately 80 kilometers) as the commencement of space.
Both of these altitudes have been suggested as the demarcation points of the upper atmosphere. Currently, there is no universally accepted international definition for the boundary of space.
The Karman line for Venus is situated at approximately 250 kilometers above the planet’s surface, while for Mars it is about 80 kilometers high. In the case of celestial bodies with minimal or no atmosphere, like Mercury, Earth’s Moon, or an asteroid, the boundary of space is considered to be the surface of the body itself.
When a spacecraft undergoes re-entry into the atmosphere, the altitude of the atmosphere is taken into account in order to calculate the trajectory and minimize its impact upon re-entry. Typically, the re-entry altitude is set at or above the Karman line. NASA utilizes a value of 400,000 feet (approximately 122 km) for this purpose.
Absolute vacuum cannot be achieved even in outer space. However, there are still a few hydrogen atoms per specific volume present. Despite this, the intensity of the cosmic vacuum is insufficient to cause a person to burst like an overinflated balloon. This is because our bodies possess enough strength to maintain their shape, although it does not prevent death from occurring.
The reason behind this is not solely strength-related. It is also not solely due to the presence of blood, even though it consists of approximately 50% water and operates within a pressurized closed system. The most that would occur is the boiling over of saliva, tears, and the fluids that moisten the alveoli in the lungs. To put it simply, a person would perish due to lack of oxygen. Even at relatively low altitudes within the atmosphere, conditions are inhospitable for the human body.
There has been a debate among scientists about the presence of a complete vacuum in space, but they unanimously agree that achieving a full vacuum is impossible due to the presence of hydrogen molecules.
The altitude at which the atmospheric pressure equals the vapor pressure of water at human body temperature, known as the Armstrong line, is approximately 19.14 kilometers. In 1966, an astronaut conducted a test of a spacesuit and was decompressed at an altitude of 36,500 meters. The spacesuit shut down within 14 seconds but did not explode and the astronaut survived.
Maximum and minimum values
In mathematics, the maximum value of a set of numbers is the largest number in that set, while the minimum value is the smallest number. These values are often used in various mathematical calculations and comparisons.
To find the maximum value, one can simply compare each number in the set to the current maximum value and update it if a larger number is found. Similarly, to find the minimum value, one can compare each number to the current minimum value and update it if a smaller number is found.
For example, let’s consider a set of numbers: 5, 9, 3, 2, 7. The maximum value in this set is 9, while the minimum value is 2.
Maximum and minimum values are important in various fields such as statistics, data analysis, and optimization problems. They help in understanding the range and extremities of a given set of data.

The baseline temperature in the vacuum of outer space, determined by the residual radiation from the Big Bang, measures 2.73 kelvin (K), equivalent to -270.45 °C.
This represents the coldest possible temperature in the vast expanse of space. Space itself does not possess a temperature, as it is merely the absence of matter and energy. To be more precise, absolute zero denotes a temperature of -273.15 °C, but within the realm of thermodynamics, achieving such a state is unattainable.
One reason why the temperature in space remains at 2.7 K is due to the presence of radiation. The temperature of the vacuum is measured based on the kinetic activity of gas, similar to how it is done on Earth. However, it is important to note that the radiation in the vacuum has a different temperature compared to the kinetic temperature of the gas. This implies that the gas and radiation are not in thermodynamic equilibrium.
Within space, the temperature can reach absolute zero, which is considered to be the lowest possible temperature.
The entirety of the observable universe is teeming with photons that originated from the momentous event known as the Big Bang. This is commonly referred to as the cosmic microwave background radiation. In addition to this, a copious amount of neutrinos, known as the cosmic neutrino background, can also be found. Currently, the background radiation’s blackbody temperature hovers around 3-4 K. The temperature of the gas in outer space is always equal to or greater than that of the background radiation, and in some cases, it can reach much higher levels. For instance, the Sun’s corona boasts temperatures that exceed a staggering 1.2-2.6 million K.
The human body
There is a common misconception related to temperature when it comes to the human body. It is well known that our body is composed of approximately 70% water. In the vacuum of space, the heat emitted by the body has nowhere to dissipate, resulting in a lack of heat exchange and causing the person to overheat.
However, before overheating becomes a concern, the individual would already have succumbed to decompression. This is why heat management is one of the challenges faced by astronauts. Even the outer skin of a spacecraft orbiting in direct sunlight can become extremely hot, with temperatures on metal surfaces reaching up to 260 °C Celsius.

Solids in the vicinity of Earth or in the space between planets are exposed to significant amounts of radiant heat when they are on the side facing the sun. When these objects are in the Earth’s shadow or on the sunny side, they experience extremely cold temperatures because they release their heat energy into the vacuum of space.
For instance, the spacesuit worn by an astronaut during a spacewalk on the International Space Station will reach temperatures of approximately 100°C on the side that is directly exposed to the sun.
On the dark side of the Earth, the sun’s radiation is obstructed, and the faint infrared radiation emitted by the Earth causes the spacesuit to cool down. In space, the temperature of the suit can drop to around -100°C Celsius.
Thermal Exchange
Note: Thermal exchange in outer space can occur solely through radiation.
This process is quite complex and is utilized to cool down the surfaces of spacecraft. The surface absorbs the radiant energy it receives and simultaneously emits energy into space, which is equivalent to the total energy absorbed plus the energy generated internally.
The exact pressure in outer space is unknown, but it is extremely low.
In the majority of galaxies, observations indicate that 90% of the mass exists in an enigmatic form known as dark matter, which interacts with other matter through gravitational forces only and not electromagnetic forces.
The majority of the mass-energy in the visible universe is the enigmatic vacuum energy of space, known as dark energy to astronomers. The vast expanse of intergalactic space fills most of the universe’s volume, while even galaxies and star systems are predominantly empty.
Uncovering

Exploration of space began in the 20th century when humans started venturing into the unknown through high-altitude balloon flights and manned rocket launches.
The first person to reach Earth orbit was Yuri Gagarin from the Soviet Union in 1961, and since then, unmanned spacecraft have successfully reached every planet in our solar system.
However, due to the expensive nature of space travel, manned missions have been restricted to low Earth orbit and the Moon.
Exploring outer space presents numerous challenges for humans, including the dangers of vacuum and radiation. Additionally, the absence of gravity in microgravity conditions has negative effects on human physiology, leading to muscle atrophy and bone loss. Furthermore, the cost of sending objects, including humans, into space is exorbitant.
What is the temperature like in space? Could it be even colder?
Temperatures in various locations throughout the cosmos
Summary
Due to the finite speed of light, there is a limit to the size of the universe that can be directly observed. This raises the question of whether the universe is finite or infinite. The universe remains an enigma, filled with numerous phenomena that are still beyond the grasp of modern science. However, the temperature in outer space has already been determined, and eventually, the pressure in space will also be measured.
The 8th International Student Scientific Conference – Student Scientific Forum 2016

ϵ – angle of the Earth’s orbit; γ – point of the spring equinox; C – point of the summer solstice; Ω – point of the autumn equinox; E – point of the winter solstice.
Therefore, the plane of the Earth’s orbit aligns with the plane of the ecliptic.
The position of the ecliptic on the celestial sphere, which refers to the equatorial coordinates α and δ of the ecliptic points and its inclination ε to the celestial equator, is determined by observing the zenith distance Zv of the Sun during its upper culmination, known as true noon. At all latitudes in the northern hemisphere of the Earth that satisfy the condition 90° > φ > δ, the Sun always reaches its highest point south of the zenith, and its smallest zenith distance occurs on the day of the summer solstice (December 22). This indicates that during these days, the Sun has the highest declination δmax = ε and the lowest declination δmin = -ε. Furthermore, since the geographic latitude always falls within the aforementioned limits:
If we look back around 3000 years ago, we can try to determine the tilt of the Earth’s ecliptic. During that time, observations in the northern hemisphere recorded that the noon altitude of the Sun on the day of the summer solstice was +63°48′, while on the day of the winter solstice it was +16°00′ south of the zenith.
How to calculate the slope using coordinates
- Ask a question
- Registration
- Technical Support
- Sign in with your username and password
- Reset your password
- Sign in with your phone
- Technical Support
Leaders
JS: 2.14.23
CSS: 4.9.13
jQuery: 3.6.0
DataForLocalStorage: 2022-06-10 01:16:03-standard
jQuery
jQuery UI
Bootstrap
Font Awesome
Alexander Babich (Professor)
Astronomy and Space
Humanities Education Problem-solving
Providing online consultation and helping to solve problems in the field of astronomy.
Online Consultation #202030
Response #1, Alexey Kotsyurbenko (Senior Moderator)
If the measurement was taken at a location with latitude φ, the zenith distance can be expressed using equatorial coordinates t (hour angle) and δ (declination) according to the equation:
Specifically, at noon (i.e., when the Sun is at its highest point in the sky) always t = 0 and
thus z = φ – δ. In turn, declination is related to ecliptic coordinates λ (astronomical longitude) and β (astronomical latitude) by a similar expression:
where ε is the inclination of the ecliptic. Since the Sun always lies in the ecliptic plane, for it β ≡ 0 and
Therefore, the Sun’s declination ranges from -ε (at λ = 270º) to ε (at λ = 90º), and its zenith distance ranges from zmin=φ-ε to zmax=φ+ε. Thus
In this case, zmin=29º48', zmax=76º42', so
The key points of the ecliptic will have the following coordinates:
α = 0º, δ = 0º – vernal equinox point (ascending node);
α = 90º, δ = 23º27' – summer solstice point;
α = 180º, δ = 0º – fall equinox point (descending node);
α = 270º, δ = -23º27' – winter solstice point.
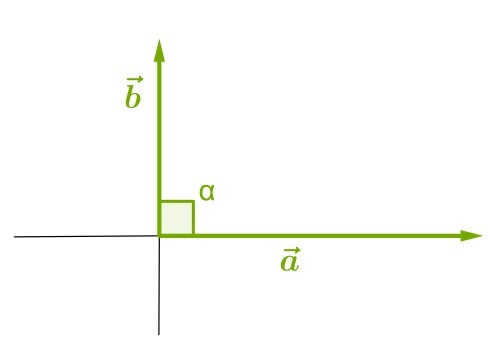
The angle formed by two vectors is the angle between the lines that represent the two vectors and originate from the same point in space. Put simply, it is the smallest angle at which one of the vectors can be rotated around its starting point to align with the direction of the second vector.
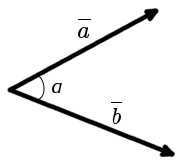
This is known as α in the image, but it can also be referred to by other labels:
Be aware! If the instructor detects plagiarism in your assignment, you will face serious consequences, possibly even expulsion. If you are unable to complete the task on your own, you can place an order here.
Similar to any other angle, the angle formed by the vectors can be expressed in various ways.
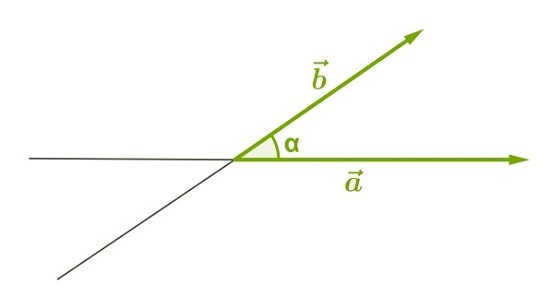
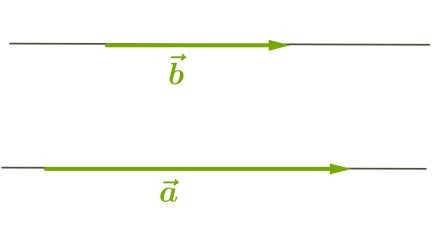
When the value is \(0^\circ\) (which means the vectors are co-directional):
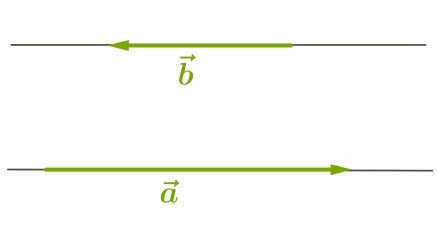
When the angle is \(180^\circ\) (vectors are pointing in opposite directions):
Calculating the angle between vectors
The angle between two vectors, \( \overrightarrow{a}\) and \(\overrightarrow{b}\), can be determined using either the scalar product or the cosine theorem applied to the triangle formed by these two vectors.
The scalar product is a value equal to the product of the magnitudes of the two vectors multiplied by the cosine of the angle between them.
The formula for the scalar product is:
\left(\left(\overrightarrow{a};\overrightarrow{b}\right)=\left \overrightarrow{a}\right \times\left \overrightarrow{b}\right \times\cos\left(\widehat{ }\right)\).
- If α is an acute angle, then the scalar product (SP) will be a positive value (since the cosine of an acute angle is positive).
- If α is an obtuse angle, the dot product will be negative (since the cosine of an obtuse angle is a negative number).
- If α is equal to 180°, meaning the vectors are oppositely directed, then the dot product is also negative, as the cosine of this angle is 1.
- If α is a right angle, then the dot product is 0 because the cosine of 90° is 0.
If both vector a and vector b are non-zero, we can determine the cosine α between them using the following formula:
Calculating the angle when a vector is given by coordinates
When the coordinates of the vectors are given as \(\overrightarrow{a}=\left(a_x;a_y
ight)\) and \(\overrightarrow{b}=\left(b_x;b_y
ight)\) on a two-dimensional plane, the angle between them can be calculated using the following formula:
If the coordinates are given in three-dimensional space as:
, then the formula for calculating the angle is as follows:
Calculation of the angle when three points are provided in a rectangular coordinate system
To better understand the explanations, let’s consider an example.
Assume we have three points and their coordinates: A(3,-2), B(2,1), C(6,-1). Our goal is to find the cosine of the angle between vector AB and vector AC.
First, we can determine the coordinates of the vectors using the given points:
Next, we can utilize the formula for calculating the cosine of an angle in a plane and substitute the known values:
Illustrations of problem solving
For the sake of clarity, let’s examine instances of resolving issues on this matter.
Issue 1
In light of the fact that \(\overrightarrow{a}\) and \(\overrightarrow{b}\) are known. Their magnitudes are 3 and 6 correspondingly, whilst their scalar product amounts to -9. Our goal is to determine the cosine of the angle between the vectors and its size.
Let’s substitute the given values:
Then ascertain the angle between these vectors:
Problem 2
Given the coordinates \(\overrightarrow{a}=(8; -11; 7)\) and \(\overrightarrow{b}=(-2; -7; 8)\) in space, we need to calculate the angle \(\alpha\) between them.
To find the cosine of the angle between two vectors in a three-dimensional coordinate system, we can use the following formula:
Substituting the given values into the formula, we can calculate the angle \(\alpha\).





