Stellar magnitude, also known as visible stellar magnitude, is a dimensionless numerical value used to describe the brightness of celestial objects, primarily stars, as seen from the observer’s location. It takes into account both the amount of light emitted by the object and its distance from the observer. Stellar magnitude serves as a metric for the brilliance of a star, with higher magnitudes indicating lower brightness and vice versa.
Definition
The modern interpretation of stellar magnitude is based on the magnitudes assigned to stars by the ancient Greek astronomer Hipparchus in the 2nd century B.C. Hipparchus categorized all stars into six magnitudes, with the brightest stars being classified as first magnitude stars and the dimmest stars as sixth magnitude stars. He evenly distributed the intermediate magnitudes among the remaining stars.
In 1856, N. Pogson proposed a formalization of the stellar magnitude scale. The visible stellar magnitude is determined by the formula:
where I represents the light flux from the object and C is a constant.
Since this scale is relative, its zero point (0 m) is defined as the brightness of a star with a luminous flux of 10³ quanta/(cm²-s-Å) in green light (UBV scale) or 10 6 quanta/(cm²-s-Å) in the entire visible light range. A star with a magnitude of 0 m outside Earth’s atmosphere creates an illuminance of 2.54-10 -6 lux.
The scale of stellar magnitudes is logarithmic because a change in brightness of the same number of times is perceived as the same (Weber-Fechner law). Additionally, because Hipparchus determined that the magnitude of the star is smaller, the brighter it is, there is a minus sign in the formula.
The following two properties assist us in the practical use of apparent stellar magnitudes:
- An increase in luminous flux by a factor of 100 corresponds to a decrease in apparent stellar magnitude by precisely 5 units.
- A decrease in stellar magnitude by one unit indicates an increase in luminous flux by a factor of 10 1/2.5 =2.512.
In the present day, apparent stellar magnitude is utilized not just for stars, but also for various other entities, such as the Moon, the Sun, and planets. Due to their potential to be brighter than the brightest star, they can possess a negative apparent stellar magnitude.
Spectral dependence
The magnitude of a star is influenced by the spectral sensitivity of the radiation receiver (such as the human eye, photoelectric detector, photographic plate, etc.).
- Visual stellar magnitude (V or mv) is determined by the sensitivity spectrum of the human eye to visible light, which is most sensitive to a wavelength of 555 nm. It can also be determined photographically using an orange filter.
- Photographic or “blue” stellar magnitude (B or mp) is determined by measuring the image of the star on a photographic plate that is sensitive to blue and ultraviolet rays. It can also be measured using an antimony-cesium photomultiplier tube with a blue filter.
- Differences in the magnitudes of the same object in different bands U-B and B-V serve as comprehensive indicators of the object’s color; the greater the differences, the redder the object appears.
The bolometric stellar magnitude is a measure of the total radiative power of a star, representing the power integrated over the entire emission spectrum. To measure it, a specialized device called a bolometer is employed.
Stellar magnitudes of a few celestial entities
| Sun | -26.7 (400,000 times brighter than the full Moon) |
| Moon at full moon | −12,7 |
| Iridium flash (maximum) | −9,5 |
| Supernova in 1054 (maximum) | −6,0 |
| Venus (maximum) | −4,4 |
| Earth (looking from the Sun) | −3,84 |
| Mars (maximum) | −3,0 |
| Jupiter (maximum) | −2,8 |
| International Space Station (maximum) | −2 |
| Mercury (maximum) | −1,9 |
| Andromeda Galaxy | +3,4 |
| The faintest stars observed with the naked eye | +6 to +7 |
| Proxima Centauri | +11,1 |
| Brightest quasar | +12,6 |
| The faintest object imaged with an 8-meter ground-based telescope. | +27 |
| The faintest object imaged with the Hubble Space Telescope. | +30 |
| Sirius | Canis Major | −1.47 |
| Canopus | Carina | −0.6 |
| Alpha Centauri | Centaurus | −0.3 |
| Arcturus | Boötes | −0.1 |
| Vega | Lyra | 0.0 |
| Capella | Auriga | +0.1 |
| Rigel | Orion | +0.2 |
| Procyon | Canis Minor | +0.4 |
| Achernar | Eridanus | +0.5 |
| Betelgeuse | Orion | +0.9 |
| Altair | Aquila | +0.9 |
| Aldebaran | Taurus | +1.1 |
| Pollux | Gemini | +1.2 |
| Antares | Scorpius | +1.2 |
| Fomalhaut | Piscis Austrinus | +1.3 |
| Deneb | Cygnus | +1.3 |
| Regulus | Leo | +1.3 |
Check out these related articles


- Main
- Stars
Stellar brightness
Even individuals who are not well-versed in astronomy are aware that stars vary in their brightness. The most luminous stars can be easily seen in a city sky illuminated by artificial lights, while the faintest stars are barely visible under ideal observing conditions.
In order to quantify the brightness of stars and other celestial objects (such as planets, meteors, the Sun, and the Moon), scientists have devised a system of stellar magnitudes.
Stellar magnitude (m; often referred to as “stellar magnitude”) is a measure of the radiation flux near the observer, indicating the observed brightness of a celestial source. This brightness is not only determined by the actual radiative power of the object, but also by its distance from the observer.
Stellar magnitude is a dimensionless quantity used in astronomy to describe the illuminance produced by a celestial object in the vicinity of the observer.
Illuminance is a measure of the amount of light flux that falls on a small surface area relative to its size. It is a unitless quantity.
In the International System of Units (SI), illuminance is measured in lux (1 lux = 1 lumen per square meter). In the centimeter-gram-second (CGS) system, illuminance is measured in foot-candles (1 foot-candle equals 10,000 lux).
The illuminance of a light source is directly related to its luminous intensity. When the source is moved further away from the illuminated surface, the illuminance decreases in proportion to the square of the distance (according to the inverse square law).
From a subjective perspective, the visible stellar magnitude is perceived as brilliance for point sources or brightness for extended sources.
In order to determine the luminosity of a source, it is compared to the luminosity of a standard source. These standards are typically non-variable stars that have been carefully selected.
The stellar magnitude was initially used to describe the apparent luminosity of stars in the optical range, but it has since been expanded to include other ranges of radiation such as infrared and ultraviolet.
Therefore, the perceived brightness of a star, also known as its apparent stellar magnitude m or luminosity, is a quantification of the amount of light illuminating a surface that is perpendicular to the rays of the star at the specific point of observation.
Historically, this concept originated more than 2,000 years ago with the ancient Greek astronomer and mathematician Hipparchus (2nd century B.C.), who categorized the stars visible to the naked eye into six different magnitudes.
Hipparchus assigned the first magnitude to the brightest stars, and the faintest stars, barely discernible to the naked eye, were given the sixth magnitude. The remaining stars were evenly distributed among the intermediate magnitudes. Additionally, Hipparchus structured the division of stellar magnitudes in such a way that stars of the first magnitude appeared significantly brighter than those of the second magnitude, just as stars of the first magnitude appeared brighter than those of the third magnitude, and so on. This means that the brightness of the stars changed consistently from one magnitude to the next.
This phenomenon is a result of the unique characteristics of human perception. For instance, if we have 1, 2, 4, 8, 16 identical light bulbs lit in a chandelier, it appears to us that the illumination in the room consistently increases by the same amount. In other words, the number of light bulbs that are turned on needs to increase the same number of times (in this case, twice) in order for us to perceive a constant increase in brightness.
The formula that expresses the logarithmic relationship between the strength of sensation E and the physical intensity of the stimulus P is as follows:
E = k log P + a, (1)
where k and a represent constants that are determined by a specific sensory system.
During the 19th century, Norman Pogson, an astronomer from England, established the scale of stellar magnitudes, incorporating the psychophysiological principles of vision.
Using empirical data, he proposed the following:
A star of first magnitude is precisely 100 times brighter than a star of sixth magnitude.
According to equation (1), the apparent magnitude of a star is determined by the following equality:
m = -2.5 lg E + a, (2)
Where -2.5 represents the Pogson coefficient, and the negative sign is a historical convention indicating that brighter stars have smaller (including negative) magnitudes. The parameter “a” represents the zero point of the magnitude scale, which is internationally agreed upon and determines the base point of the scale.
If E1 and E2 correspond to stellar magnitudes m1 and m2, then equation (2) implies the following relationship:
E2/E1 = 10 0.4(m1- m2) (3)
When the difference in stellar magnitudes, m1 – m2, is decreased by 1 unit, the luminosity E increases by a factor of approximately 2.512. For m1 – m2 = 5, which corresponds to a range of magnitudes from 1 to 6, the change in illuminance will be E2/E1=100.
The classical form of Pogson’s formula establishes the relationship between the apparent stellar magnitudes:
This equation allows for the calculation of the difference in stellar magnitudes, rather than the magnitudes themselves.
In order to establish an absolute scale, it is necessary to define a zero point, which corresponds to a specific luminosity that corresponds to a stellar magnitude of zero (0 m). Initially, the luminosity of Vega was used as the zero point. Subsequently, the zero point was redefined, but Vega still serves as a standard for zero apparent stellar magnitude in visual observations (according to the current system, in the V band of the UBV system, its luminosity is +0.03 m, which is practically indistinguishable from zero to the naked eye).
Typically, the zero point of the stellar magnitude scale is determined conventionally by a set of stars that undergo careful photometry using various methods.
Furthermore, I am completely confident that an illuminance of 0 m is equivalent to an energy value of E=2.48*10 -8 W/m². In reality, this is the luminosity that astronomers measure during their observations, and then it is purposely converted into stellar magnitudes.
This is done not only because “it is more customary,” but also because the concept of stellar magnitude has proven to be incredibly convenient.
stellar magnitude has proven to be an incredibly convenient concept.
Measuring luminosity in watts per square meter is excessively burdensome: for the Sun, the measurement ends up being significant, while for faint telescopic stars, it is minuscule. Conversely, working with stellar magnitudes is significantly simpler, as the logarithmic scale allows for the effortless representation of immense ranges of magnitude values.
The Pogsonian formalization later became the accepted approach for estimating stellar magnitudes.
It is a fact that the current scale is not restricted to only six stellar magnitudes or visible light. Objects that are incredibly bright can have a stellar magnitude that is negative. For instance, Sirius, which is the brightest star in the sky, has a stellar magnitude of -1.47 m. The modern scale also assigns values to the Moon and Sun: a full Moon has a stellar magnitude of -12.6 m, while the Sun has a stellar magnitude of -26.8 m. The Hubble orbiting telescope has the ability to observe objects with a luminosity of up to approximately 31.5 m.
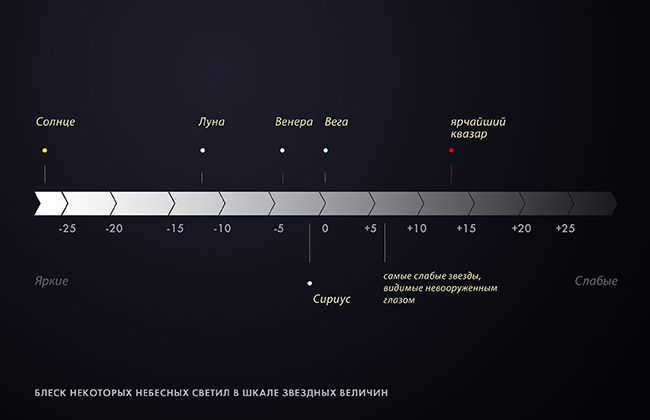
Scale of stellar brightness
(the scale is opposite: smaller values correspond to brighter objects)
Visible brightness of some celestial bodies
Sun: -26.73
Moon (at full moon): -12.74
Venus (at maximum brightness): -4.67
Jupiter (at maximum brightness): -2.91
Sirius: -1.44
Vega: 0.03
Faintest stars visible to the naked eye: about 6.0
Sun from 100 light years away: 7.30
Proxima Centauri: 11.05
Brightest quasar: 12.9
Faintest objects captured by the Hubble telescope: 31.5
Sources – Wikipedia
Stellar brightness

Currently, there are additional cumulative discounts (ranging from 2% to 25%) available for 58,742 educational institutions. To determine the discount applicable to all staff members in your educational institution, please log in to your personal Infoworks account.




Professional development course
Finger exercises as a tool for enhancing language skills in preschool children.
We can apply your educational institution’s discount to this offer (the amount will depend on how many of your colleagues have completed an Infoworks course).
Currently, 58,742 educational institutions are eligible for additional discounts ranging from 2% to 25%. To find out the specific discount available for all employees of your educational institution, please log in to your personal Infoworks account.


The retraining course for professionals is available.
Engaging in the design and implementation of educational processes in various educational organizations (specifically in the field of “Fine Arts and Technology”).
In addition to this discount, your educational institution may also have its own discount, depending on how many of your colleagues have enrolled in Infowork courses.
Currently, 58,742 educational institutions are eligible for additional discounts, ranging from 2% to 25%. To find out the specific discount applicable to all employees of your educational institution, please log in to your personal Infoworks account.


Creating a Connection Between Play and Music for Preschool-Aged Children with Sensory Integration Disorders and Disabilities
Slide-by-Slide Presentation Breakdown:


Slide 3: The luminosity L or radiative power is the total energy emitted by a star per unit time.


Slide number 4 states that a star can appear bright under the following conditions:
1) it is located near the observer;
2) it possesses a considerable amount of luminosity.

The measurement unit for a star’s luminosity is known as visible stellar magnitude, and it is inversely proportional to the star’s luminosity. In other words, the higher the luminosity, the lower the magnitude, and vice versa.

There are 6 categories of visible stellar magnitude as classified by Hipparchus. These categories include the brightest stars, which are referred to as stars of the first magnitude.


Slide 9 In the present day, the concept of apparent stellar magnitude is not limited to stars alone, but extends to encompass various celestial bodies like the Moon, Sun, and planets. Since these objects can sometimes emit more light than even the brightest star, their apparent stellar magnitude can be negative.

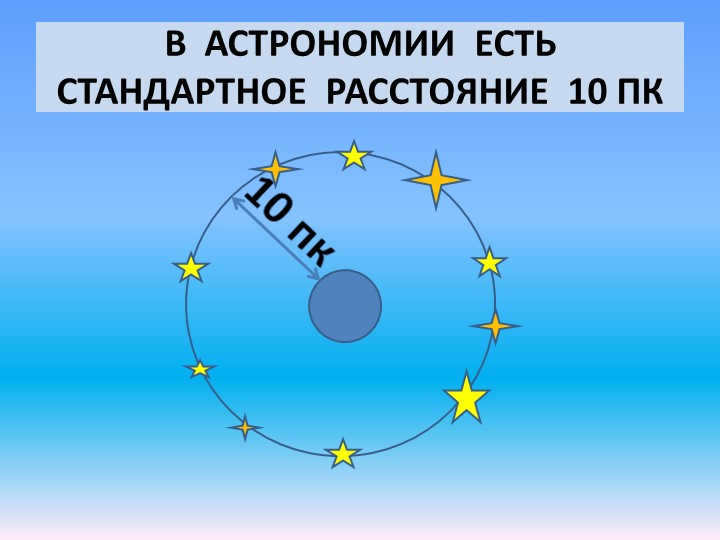

12 slide The absolute magnitude of a star is the apparent magnitude that a star would have if it were located at a distance of 10 parsecs from Earth.

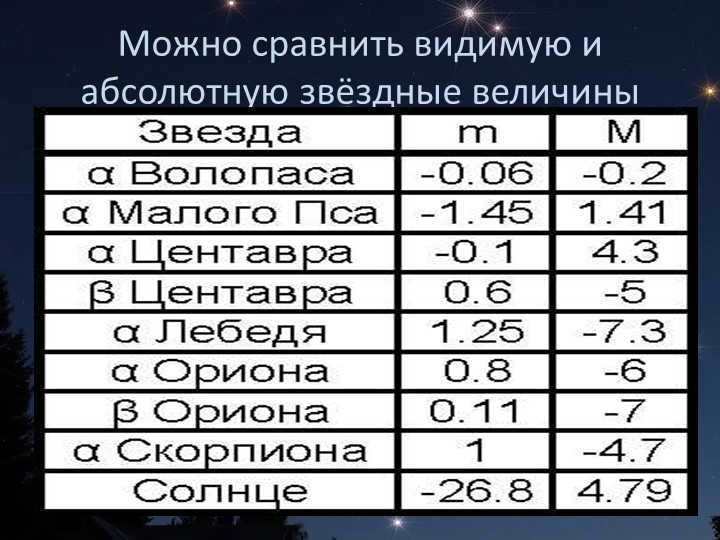


On slide 17, there is a range of absolute stellar magnitudes for stars, ranging from -9m to 19m. This means that they differ by 28m or, in terms of luminosity, by a factor of 160 billion.

On slide 18, you will find the formula for computing the luminosity of stars. The luminosity of our Sun is equivalent to 3.846∙10²⁶ watts per second. Additionally, the Sun has an absolute stellar magnitude of 5.


Discover resources for any lesson by specifying your subject (category), grade, textbook, and topic:
There are 6,330,785 materials available in our database.
This material is suitable for UMK.
Subject
Other materials
- Textbook: “Astronomy (basic level)”, by Vorontsov-Vel’yaminov B.A. and Straut E.K.
- Topic: Section 2 – Observations: the foundation of astronomy
- Textbook: “Astronomy (basic level)”, by Vorontsov-Veliaminov B.A. and Straut E.K.
- Topic: 5. The Sun and stars
- Textbook: “Astronomy (basic level)”, by Vorontsov-Veliaminov B.A. and Straut E.K.
- Topic: Section 20 – Small bodies of the solar system
You may find these courses appealing:
- Professional development course on “Fundamentals of project management in the implementation of FSES”
- Professional retraining course on “Clinical psychology: theory and methodology of teaching in an educational organization”
- Professional retraining course on “Organization of personnel selection and assessment activities (recruiting)”
- Professional development course on “Economics: Controlling Tools”
- Advanced training course on “Specifics of teaching astronomy at secondary school”
- Advanced training course on “Insurance and actuarial calculations”
- Professional retraining course on “Astronomy: Theory and Methodology of Teaching in Educational Organization”
- Retraining course “Organization of technical support for clients in the installation and operation of information and communication systems”.
- Professional retraining course “Activity on storage of museum objects and museum collections in museums of all kinds”.
- Professional retraining course “Organization of the activity of a specialist appraiser-expert in property appraisal”
- Professional retraining course “Organization of water disposal and wastewater treatment activities”
- Professional retraining course “Organization of insurance (reinsurance) process”
- Professional Retraining Course “Quality Management”
- Professional retraining course “Strategic management of remote information and reference service”
Write a comment
- 07.04.2019 11148
- PPTX 5 mbytes
- 506 downloads
- Rating: 2 out of 5
- Give a rating to the content:
If you believe that the content violates copyright or should be removed from the site for any other reason, you can file a complaint about the content. Remove content
Author of the material
- Site membership: 7 years and 7 months
- Number of subscribers: 20
- Total views: 532402
- Total materials: 151
27 minutes
18 minutes
Music Masterclass – Beginner Lessons: Working on Technique with Etude Examples. Exercises to Improve Technique
31 minutes
Gift Vouchers
The responsibility for resolving any conflicts regarding the materials and their content lies with the users who uploaded the materials on the website. However, the site administration is prepared to offer full assistance in resolving any matters related to the functioning and content of the website. If you come across any unauthorized use of materials on this site, please notify the site administration through the provided feedback form.
All content published on this website is either created by the website’s authors or contributed by its users, and is provided solely for informational purposes. The copyrights for all materials belong to their respective legal authors. Any unauthorized reproduction or distribution of the website’s materials, in whole or in part, is strictly prohibited without written permission from the website’s administration. The views expressed by the administration may not necessarily align with those of the authors.
Definition [ edit ]
During the 2nd century BC, the ancient astronomer Hipparchus of Greece classified all stars into six different magnitudes. He referred to the brightest stars as first magnitude stars, the dimmest stars as sixth magnitude stars, and evenly distributed the remaining stars among the intermediate magnitudes.
It was later discovered that the relationship between this scale and actual physical magnitudes is logarithmic, as the eye perceives a change in brightness by the same amount when it changes by the same number of times (according to the Weber-Fechner law). In 1856, Norman Pogson proposed the following formalization of the scale of stellar magnitudes, which became widely accepted:

5\, \mathrm \left( \frac
ight)
The objects’ stellar magnitudes (m) and luminosities (L) are related in such a way that a 5-unit increase in stellar magnitude corresponds to a 100-fold drop in light flux.
This definition allows us to determine the difference in stellar magnitudes, but not the magnitudes themselves. To establish an absolute scale, a zero point must be set – the luminosity that corresponds to zero stellar magnitude (0 m). Initially, Vega’s luminosity was chosen as the zero point. Although the zero point has been redefined, Vega still serves as a reference for zero apparent stellar magnitude in visual observations (in the V band of the UBV system, its luminosity is +0.03 m, which is practically zero to the naked eye).
Based on current measurements, a star with an apparent magnitude of zero outside of Earth’s atmosphere emits an illuminance of 2.54-10 -6 lux. The brightness of such a star is roughly 10 3 quanta/(cm²-s-Å) in the green light spectrum (band V of the UBV system) or 10 6 quanta/(cm²-s) across the entire visible light range.
The following characteristics facilitate the practical use of visible stellar magnitudes:
- An increase in luminous flux by a factor of 100 corresponds to a decrease in apparent stellar magnitude by exactly 5 units.
- A decrease in stellar magnitude by one unit indicates an increase in luminous flux by a factor of approximately 2.512.
In modern times, the notion of stellar magnitude is employed not just for stars, but also for other celestial bodies including the Moon, Sun, and planets. The stellar magnitude of the most luminous objects is represented by negative values. For instance, the luminosity of the Moon during a full phase reaches -12.7 m, while the luminosity of the Sun is -26.7 m.
Concept of Stellar Magnitude [ edit ]
The concept of stellar magnitude can be divided into two categories: apparent and absolute magnitude. Apparent magnitude (m) refers to the brightness of a star as observed from Earth, while absolute magnitude (M) represents the intrinsic brightness of a star if it were located 10 parsecs away from the observer. Unlike apparent magnitude, absolute magnitude allows for the comparison of the luminosity of different stars, as it is not influenced by their distance.
It is important to note that the term “apparent magnitude” is used to differentiate it from absolute magnitude, and can be applied to magnitudes measured in various ranges, including ultraviolet, infrared, or other specific wavelengths. However, when referring to magnitudes measured in the visible range, the term “visual magnitude” is used. For instance, the absolute bolometric stellar magnitude of the Sun is +4.8 m, while its apparent magnitude is -26.7 m.
The magnitude of a star is determined by the spectral sensitivity of the radiation receiver, such as the eye, photoelectric detector, or photographic plate.
- Bolometric stellar magnitude represents the total radiative power of a star across all wavelengths. It is measured using a specialized device called a bolometer. This magnitude is particularly relevant for stars that emit predominantly in the non-visible spectrum, such as very hot or very cold stars.
However, most stellar magnitudes are measured within specific wavelength intervals. Photometric systems have been developed for this purpose, each consisting of a set of bands that cover different ranges of wavelengths. Within each band, the sensitivity is highest at a particular wavelength and gradually decreases as the distance from that wavelength increases.
The UBV system is the most widely used photometric system, comprising of three bands that cover different wavelength ranges. This system allows for the measurement of three stellar magnitudes for each object:
- Visual stellar magnitude (V) represents the brightness of an object in the V filter, which has a transmission maximum close to the peak sensitivity of the human eye (555 nm).
- “Blue” stellar magnitude (B) indicates the brightness of an object in the blue region of the spectrum, with maximum sensitivity at a wavelength of approximately 445 nm.
- Ultraviolet stellar magnitude (U) has its maximum sensitivity in the ultraviolet region at a wavelength of around 350 nm.
Differences in the magnitudes of a star in different bands, such as U-B and B-V in the UBV system, can be used to determine the color of the star. The larger the differences, the redder the star is. In the UBV photometric system, stars of spectral class A0V have color indices of zero.
There are other photometric systems that use different sets of magnitudes to classify stars.
- The photographic stellar magnitude is determined using unsensitized photographic emulsion with maximum sensitivity at a wavelength of 425 nm. It coincides with the visual stellar magnitude for A0V stars and has a brightness of (6.0±0.5) m. It was used in the outdated photographic system of stellar magnitudes along with the photovisual stellar magnitude.
Stellar brightness of selected objects [ edit ]
| Sun | -26.7 (400,000 times brighter than the full Moon) |
| Moon at full moon | −12.74 |
| Iridium flash (maximum) | −9.5 |
| Supernova in 1054 (maximum) | −6.0 |
| Venus (maximum) | −4.67 |
| International Space Station (maximum) | −4 |
| Earth (viewed from the Sun) | −3.84 |
| Jupiter (maximum) | −2.94 |
| Mars (maximum) | −2.91 |
| Mercury (maximum) | −2.45 |
| Saturn (with rings; maximum) | −0.24 |
| Stars of the Big Dipper | +2 |
| Andromeda Galaxy | +3.44 |
| Jupiter’s satellites | +5-6 |
| Uranus | +5.5 |
| The faintest stars observable naked eye | +6 to +7.72 |
| Neptune | +7.8 |
| Proxima Centauri | +11.1 |
| Brightest quasar | +12.6 |
| The faintest object imaged with an 8-meter ground-based telescope. | +27 |
| The faintest object imaged with the Hubble Space Telescope. | +31.5 |
Related Articles [ edit ]
Additional Information [ edit ]
- ↑ Stars / Surdin V. G. . Г. . – Moscow: Fizmatlit, 2009. – P. 63.
- ↑ 2,02,1Surdin V. G. Г. .Stellar brightness (Russian) . Glossary Astronet.ru. Verified on September 16, 2012.Archived from the original source on November 28, 2010.
- ↑ Calculated assuming that the stellar brightness at a distance of 1 a. e. is -26.7, which corresponds to the Sun's absolute stellar brightness of +4.87.
References [ edit ]
- Mironov A. В.Precision photometry. “Astronet. Verified on August 28, 2012.Archived from the original source on October 17, 2012.
- Determining stellar magnitude in an image. “Astrotourist”. Verified on November 20, 2009.Archived from the original source on May 11, 2012.
Stars are located millions of times farther away from the Sun, which means that the horizontal parallaxes of stars are millions of times smaller. Due to the extremely small angles involved, no one has been able to successfully measure these parallaxes. In order to determine the distances to stars, astronomers rely on the annual parallaxes caused by the Earth’s orbital motion around the Sun (Fig. 13.1).
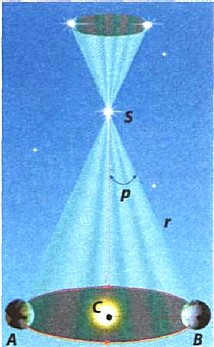
Figure 13.1: The angle at which the major semi-axis of the Earth’s orbit (1 a. e.) would be observed from a star in a direction perpendicular to the line of sight can be determined by the annual parallax.
The Sun is located at point C; A and B represent the Earth’s positions in its orbit at intervals of 6 months; BC = 1 a. e. is the distance from the Earth to the Sun (the major semi-axis of the Earth’s orbit); S is the star for which the distance needs to be determined; angle BSC = p represents the star’s annual parallax.
The distance from the Earth to the star can be calculated using the right triangle CBS:
The annual parallax can only be measured for a few months, as the Earth, along with the telescope, moves around the Sun in outer space.
In Copernicus’ time, astronomers made attempts to determine the annual parallaxes of stars. This could have served as irrefutable evidence of the Earth’s revolution around the Sun and confirmed the heliocentric system of the world. However, it was not until 1837 that V. Struve, at the Pulkovo Astronomical Observatory in Russia, successfully determined the annual parallax of the star Vega in the constellation Lyra. The nearest star, Proxima Centauri, has the largest parallax at p = 0.76″, but it is not visible in Europe. Among the bright stars observable in Ukraine, the closest to us is Sirius in the constellation Canis Major (Big Dog), with an annual parallax of p = 0.376″.
The distance to stars is typically measured in light years (see “Light years” §1). However, in astronomy, the unit parsec (pk) is still used. It is defined as the distance for which the annual parallax p is equal to 1″ (parsec being short for parallax-second).
The relationship between a parsec and a light-year can be defined as 1 parsec equals 3.26 light-years. When measuring the annual parallax in angular seconds, the distance to the stars in parsecs can be calculated using the following formula:
Stellar Magnitudes that are Visible
The concept of stellar magnitude was initially introduced in the 2nd century BC by Hipparchus, a Greek astronomer, to measure the brightness of stars. During that time, astronomers believed that all stars were equidistant from Earth, and their brightness was determined solely by their size. However, we now know that stars within the same constellation can be at varying distances from us (Fig. 2.2). As a result, the apparent stellar magnitude only represents the amount of energy our eyes perceive from a star over a specific time period. Hipparchus categorized all visible stars into six distinct classes of brightness, known as stellar magnitudes. The brightest stars were classified as first magnitude, followed by second magnitude for slightly dimmer stars, and so on. The faintest stars, which can barely be seen in the night sky, are categorized as sixth magnitude. In the 19th century, the English astronomer N. Pogson (1829-1891) introduced an additional criterion for stellar magnitude. According to his definition, stars of the first magnitude must be 100 times brighter than stars of the sixth magnitude (Fig. 13.2).

Figure 13.2: Stars in the vicinity of Polaris serve as a standard for determining the apparent magnitudes of stars
The apparent magnitude of a star is represented by the letter t. For any given magnitude, the ratio of its brightness E1 and E2 is:
The visible magnitude m determines the amount of light that reaches our eyes from a star. The faintest stars that can still be seen with the naked eye have a magnitude of m = +6. Equation (13.4) is known as Pogson’s formula. The brightness E actually represents the illumination generated by the star on the Earth’s surface, so the value of E can be measured in lux – the units of illumination used in physics. According to formula (13.4), if the difference in magnitudes of the two stars is equal to one, the brightness ratio will be approximately 2.512.
In order to determine the apparent magnitudes of stars in the sky, astronomers have established a standard using the north polar series. These stars, totaling 96, are located around the North Pole of the Earth. Among them, the brightest star, Polaris, has a stellar magnitude of m = +2 m (Fig. 13.2). By comparing other stars to this standard, astronomers can determine their apparent magnitudes. Stars that are faint but still visible to the naked eye have a stellar magnitude of +6 m, while stars up to +8 m can be seen with binoculars. Luminaries with magnitudes up to +11 m can be observed using a school telescope, and with the help of the largest telescopes, modern methods can detect faint galaxies with magnitudes up to +28 m. On the other hand, very bright celestial objects have negative stellar magnitudes. For example, the brightest star in our sky, Sirius, has an apparent magnitude of m = -1.6 m, while the brightest planet, Venus, has a magnitude of m = -4.5 m. The Sun, being the brightest object in our solar system, has a magnitude of m = -26.7 m.
Astrophysical brilliance and the radiance of celestial bodies
Even though the Sun is the brightest celestial body in our sky, that doesn’t mean it emits more energy than other stars. According to the laws of physics, the amount of luminosity produced by energy sources depends on the distance from them. This means that a small light bulb in your room might appear much brighter than a distant spotlight. To calculate the total radiative power, or luminosity, astronomers use the concept of absolute stellar magnitude M. The absolute stellar magnitude is the magnitude a star would have at a standard distance r0 of 10 parsecs. One star that is approximately at this distance (11 pc or 36 light years) from us is Arcturus, which has an apparent stellar magnitude that is almost equal to its absolute stellar magnitude. If the Sun were at a distance of 10 parsecs, it would have the appearance of a rather faint star with a fifth stellar magnitude. This means that the absolute stellar magnitude of the Sun is approximately 5 m. By knowing the distance to a star r in parsecs and its apparent stellar magnitude m, we can use the following formula to determine its absolute stellar magnitude M:
The brightness of a star is what determines how much energy the star emits over a given period of time, also known as the star’s radiative power. In astronomy, the unit of measurement for brightness is based on the Sun’s radiative power, which is approximately 4-10 26 W. If the absolute magnitude of a star M is known, its brightness can be calculated using the following formula:
The temperature of a star can be calculated by applying the principles of blackbody radiation (refer to section 6). The most straightforward approach to determining a star’s temperature is by examining its color. However, our naked eye can only perceive the color of bright stars due to its limited sensitivity in low light conditions. Using binoculars or a telescope, which capture more light, allows us to determine the color of faint stars. As a result, stars appear brighter to us when viewed through the eyepiece of a telescope.
To categorize stars based on temperature, they have been divided into seven spectral classes (see Figure 13.3). These classes are denoted by letters from the Latin alphabet: O, B, A, F, G, K, M (remember the English proverb: “Oh, Be A Fine Girl, Kiss Me”).

Figure 13.3: The 7 main spectral classes determine the colors of stars. Stars that are hot and blue belong to spectral class O, while stars that are cool and red belong to spectral class M. The Sun, with a photospheric temperature of +5780 K and a yellow color, belongs to spectral class G.
Stars that are blue and belong to spectral class O emit more energy in the blue part of the spectrum and have the highest surface temperature (Fig. 13.4). Each spectral class is further divided into 10 subclasses: AO, A1..A9.
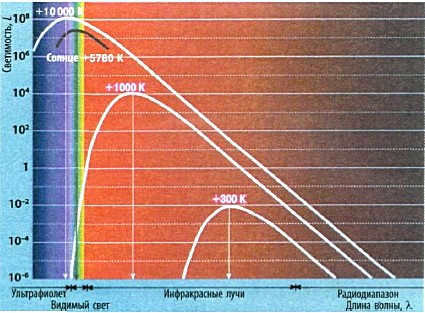
Fig. 13.4. Cosmic bodies emit radiation with varying intensity based on their temperature. High temperature stars emit more energy in the blue spectrum, while low temperature stars emit more energy in the red spectrum. Planets primarily emit energy in the infrared spectrum.
Typically, the spectrum of each star contains dark absorption lines, which are formed in the rarefied atmosphere of the star and in the Earth’s atmosphere, and they indicate the chemical composition of these atmospheres. It has been discovered that all stars have nearly identical chemical compositions, as hydrogen and helium are the primary elements in the Universe. The main difference between different spectral classes lies in the temperature of the stellar photospheres.
Radii of stars
The radius of a star cannot be determined using the geometric method due to the vast distance between stars and Earth. Even with powerful telescopes, it was not possible to measure the angular sizes of stars until recently. This is because all stars appear as identical bright points. In order to determine the radius of a star, astronomers rely on the Stefan-Boltzmann law:
where Q represents the energy radiated by a unit of the star’s surface per unit of time, σ is the Stefan-Boltzmann constant, and T is the absolute temperature of the star’s surface.
The power radiated by a star with a radius R is determined by the surface area, which can be expressed as:
On the other hand, we can apply the same equation to calculate the power radiated by the Sun:
Therefore, by using Equations 13.8 and 13.9, it is possible to determine the unknown radius of a star if the radius and temperature of the Sun are known:
It has been discovered that there exist stars whose radius is hundreds of times greater than the radius of the Sun, as well as stars whose radius is smaller than that of the Earth (Fig. 13.5).

Figure 13.5: Comparison of star radii with the Sun
Diagram illustrating the relationship between spectrum and luminosity
The Sun is an ordinary celestial body in terms of its physical characteristics – it possesses average temperature, average luminosity, and so on. From a statistical standpoint, among the numerous celestial bodies, the majority of them exhibit average characteristics. To illustrate, if one were to measure the height and weight of a large number of individuals of various ages, there would be a greater number of individuals with average values for these parameters. Astronomers set out to investigate whether there are a significant number of stars similar to our Sun in the vastness of the universe. To accomplish this, E. Herzsprung (1873-1967) and G. Ressel (1877-1955) proposed a diagram that allows for the plotting of each star’s position based on its temperature and luminosity. This diagram came to be known as the spectrum-luminosity diagram, or the Hertzsprung-Ressel diagram. It takes the form of a graph, with the horizontal axis representing the star’s spectral class or temperature, and the vertical axis representing its luminosity (Fig. 13.6).
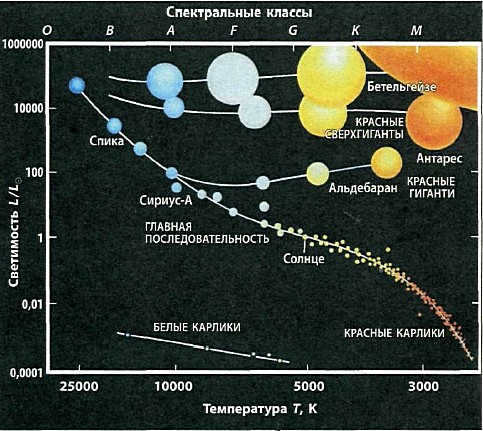
Figure 13.6 showcases the Hertzsprung-Russell diagram, which depicts the relationship between the temperature and luminosity of stars. The temperature is represented on the x-axis, while the y-axis represents the luminosity. For reference, the Sun is positioned at a temperature of 5780 K and a luminosity of 1. On the diagram, colder stars (red) are situated on the right side, while hotter stars (blue) are located on the left side. Stars that emit more energy are positioned above the Sun, while dwarf stars can be found below. The majority of stars, including the Sun, fall within a narrow range known as the main sequence of stars.
Red dwarfs are stars that have masses smaller than the Sun but larger than Jupiter. These stars maintain a constant temperature and luminosity for billions of years.
On the diagram, there are separate categories for white dwarfs (bottom left) and red supergiants (top right). Despite having similar masses, these stars differ greatly in size. Spectral class M giants have a similar mass to spectral class B white dwarfs, but their average densities vary significantly. For example, the red giant Betelgeuse has a radius 400 times that of the Sun, but its mass is almost the same. This means that red giants of spectral class M have an average density millions of times lower than that of Earth’s atmosphere. A typical example of a white dwarf is Sirius’ companion.
For those who are curious.
The primary enigma of the spectrum-luminosity diagram is that in outer space, astronomers have yet to discover a pair of stars with identical physical characteristics – such as mass, temperature, luminosity, and radius. It is likely that stars undergo changes in their physical properties during their evolution, making it improbable to come across another star in the universe that was born at the same time as our Sun, with identical initial properties.
Conclusions
The characteristics of stars, such as luminosity, temperature, radius, and density, vary greatly. These characteristics are interconnected and reflect the star’s evolutionary path. The Sun, for example, falls into the category of yellow stars that maintain a stable size over billions of years. In contrast, there are giant stars in space that are thousands of times larger than the Sun, as well as dwarf stars with a radius smaller than that of the Earth.
Tests
- What units are used by astronomers to measure the distance to stars?
- a. Kilometers.
- b. Astronomical units.
- c. Parallaxes.
- d. Light years.
- e. Parsecs.
- What does apparent stellar magnitude determine?
- a. The luminosity of a star.
- b. The radius of the star.
- c. The brightness of the star.
- d. The illumination that the star creates on Earth.
- e. The temperature of the star.
- At what distance do absolute and apparent stellar magnitudes have the same value?
- a. 1 a. e.
- b. 10 a. e.
- c. 1 sv. year.
- d. 10 sv. years.
- e. 1 pc.
- f. 10 pc.
- Which spectral class of stars has the highest temperature at the surface?
- a. A;
- b. B;
- c. F;
- d. G;
- e. K.
- Select the surface temperature and spectral class to which the Sun belongs:
- a. 5,500 K and G.
- b. 10,000 K and B.
- c. 2,000 K and M.
- d. 8,000 K and F.
- e. 6,000 K and A.
- Which stars have the highest surface temperatures and to which spectral class do they belong?
- What is the distinction between apparent and absolute stellar magnitudes?
- How do astronomers measure the temperature of stars?
- Which color stars have the highest surface temperature? What is the lowest temperature?
- Are there any stars with masses smaller than Earth’s mass? Do they have a radius smaller than Earth’s radius?
- Calculate the radius of one of the bright stars visible on the evening of your birthday. How would this star appear in our sky if it were in the position of the Sun?
Key concepts and terms:








