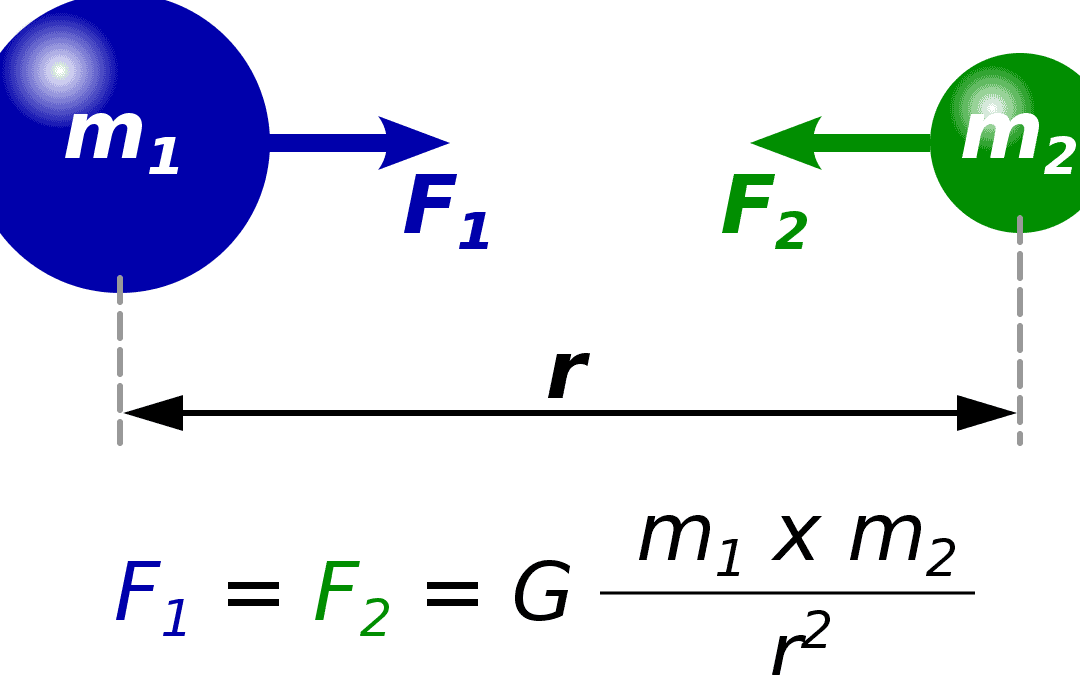In the contemporary expression of the law of universal gravitation, there exists a factor, known as the constant of gravity, that distinguishes itself by appearing before the formula. It is fascinating to note that Newton, the individual who first discovered the law of attraction, did not utilize the explicit value of the constant, as its numerical value was not determined until more than a century after the scientist’s passing.

Explanation of the gravitational constant
The gravitational constant is a fundamental physical constant that appears in the formula of the law of universal gravitation, which is commonly taught in school mechanics. It represents the strength of the gravitational force between two objects and is denoted by the symbol G.
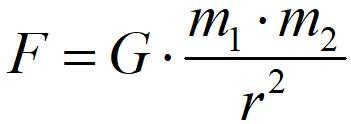
The gravitational constant, denoted by G, is a coefficient of proportionality in the law of universal gravitation.
In the law of universal gravitation, the masses of two bodies experiencing mutual attraction are represented by m1 and m2.
The coefficient of proportionality, G, represents the force with which a pair of kilogram objects located a meter apart are attracted to each other.
The value of the gravitational constant is usually taken to be equal to a specific numerical value.
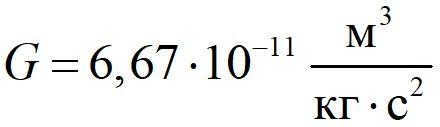
The reason why people in the vicinity do not feel the force of gravity, despite its constant action, is because the force is only manifested on objects with enormous masses, such as planets, the Sun, and other stars. This small number explains the lack of gravitational force experienced by people in everyday situations.

Measurement units for the gravitational constant
Despite the fact that the numerical value of the gravitational constant equals the force, it is not measured in newtons. The units of measurement for this coefficient may appear intimidating.
According to the International System of Units (SI), force is measured in newtons, i.e.
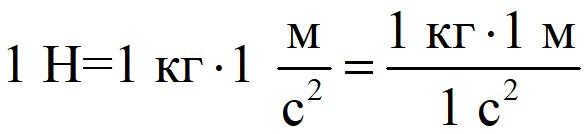
In other words, the gravitational constant determines that 1 newton is the amount of force that can change the velocity of a kilogram object by 1 m/s in just one second.
Once the law of gravitation was discovered, it was determined that two kilogram bodies are attracted to each other by a force whose value depends inversely on the square of the distance between them.
This means that the unit of gravitational force is defined as-
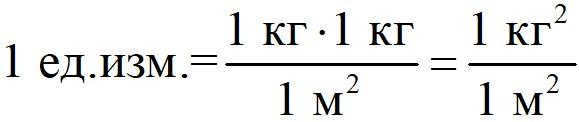
However, the dimensionalities do not align with the standard ones. We require a coefficient that can harmonize the units of measurement for both the normal force and the gravitational interaction force.
Let’s perform the necessary calculations ourselves.
We aim to equate
and .
To accomplish this, we can divide by 1s^2 and 1kg, and then multiply by m^3, resulting in:
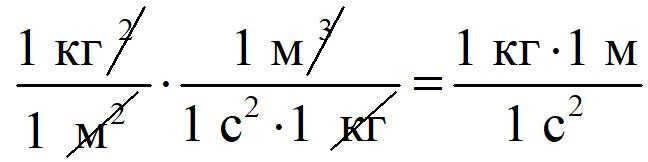
The necessary dimensionality is achieved.
Therefore, the constant possesses dimension .
Methods for determining the gravitational constant – historical background
Coefficient G is an unchanging universal constant, which is determined through experimental measurement. The discovery of the value of the gravitational constant is attributed to an unknown individual, with the first documented use in Poisson’s “Treatise on Mechanics” dating back to 1811.
Newton’s Contribution
When Newton published his treatise on the law of gravitation, he did not explicitly mention the constant that represents gravity and its effects. It was only in the late eighteenth century that this coefficient started to appear in physics literature, and its precise value was yet to be determined.

Instead of the gravitational constant that is commonly known today, there existed a gravitational parameter:
M – the mass of an object, specifically the mass of a planet or a star, as the gravitational parameter became widely used in the field of astrophysics.
Currently, for objects within the Solar System, the value of this parameter is calculated with greater accuracy compared to the gravitational constant G and the individual masses. This calculation does not require extensive experiments, but is instead based on astronomical observations.
- For the Earth
 ;
; - Moon;
- Sun
 .
.
You can find additional information regarding the application of the law of universal gravitation in astronomy in our article.
The Cavendish experiment and the experimental determination of the gravitational constant
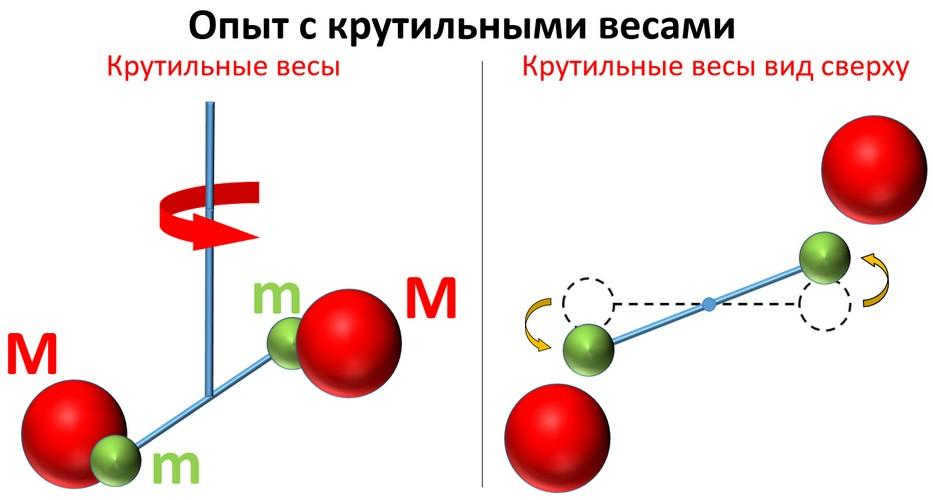
Naturalist John Mitchell initially proposed an experiment to calculate the mass of the Earth using torsion weights, although he was unaware of it at the time. Following his passing, the concept of the experiment and the apparatus were inherited by English physicist and chemist Henry Cavendish. Cavendish made improvements to the device and conducted a series of experiments, ultimately bringing Mitchell’s idea to fruition.

The measured value of the gravitational force was 0.17 micronewton, which, when compared to the weight of a small ball, is approximately 45 million times smaller.
Henry Cavendish’s experiment resulted in the calculation of the average density of the Earth, with an impressive accuracy – the measured value deviated from the modern value by only 0.7%. Although Cavendish is often credited with discovering the gravitational constant, it was not his primary goal during his experiments. It is believed that the value of the constant was derived from his experiment’s results, but the true originator of this discovery remains unknown.
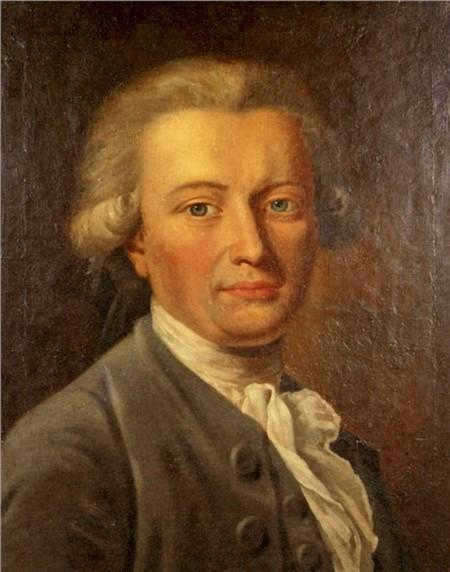
Determining the value of the gravitational constant
![]()
Different sources provide varying values for the gravitational constant derived from Cavendish’s measured density. According to the Encyclopedia Britannica, the number is equal to , a value accepted by some modern physicists. Leon Neil Cooper states that the experimentally obtained number is , while Oleg Pavlovich Spiridonov, in his collection of constants, gives a value of .
The coefficient of proportionality was determined by Henry Cavendish, and his setup has since been modernized with new materials. For example, in 1872, Cornu and Bayle used platinum small balls and glass filled with mercury to measure the gravitational constant. The experiment yielded a value of .
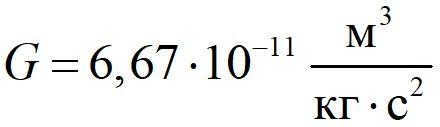
with an approximate error of 5*10 -3 .
The recent history of modifications in the gravitational constant
The gravitational constant is a decimal fraction that is constantly being refined, and the determination of the G coefficient is achieved through improvements in the Mitchell instrument and observational techniques. For instance, in 2018, scientists from Russia and China conducted experiments using different apparatus designs. The first team employed the “time of swing” (TOS) approach, where the proportionality coefficient is dependent on the oscillating frequency of the pendulum. The second team utilized the “angular acceleration feedback” (AAF) method, which measures the angular acceleration of independently rotating ball arms through a feedback control system while ensuring that the thread remains untwisted.

Based on the findings of the team, the initial approach yielded a measurement for the gravitational constant. ![]() , while the second approach produced
, while the second approach produced ![]() . The relative error was 11.6*10 -6
. The relative error was 11.6*10 -6
In 2020, the Committee on Data for Science and Technology (CODATA) recommended a coefficient of proportionality value equal to .
Thus, the value of the gravitational constant is continuously being refined, necessitating the development of new and more precise methods for its measurement and calculation.
The gravitational constant, also known as Newton’s constant (often denoted as G or sometimes GN or γ) [1], is a fundamental physical constant that describes the strength of the gravitational interaction.
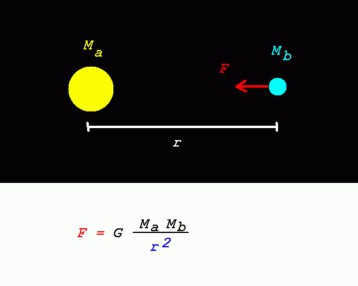
According to Newton’s law of universal gravitation, the force of gravitational attraction F between two objects with masses m1 and m2 located at a distance r is given by the equation:
![F=G\frac<m_1 m_2></p>
Proportionality coefficient [ZEBR_TAG_i>G</i> in this formula is known as the <b>gravitational constant</b>. Numerically, it is equivalent to the magnitude of the gravitational force acting on a unit mass point body by another body with the same mass at a unit distance from it.</p><p>In the International System of Units (SI), the value recommended by the Committee on Data for Science and Technology (CODATA) [3] for 2008 was</p><p><i>G</i> = 6.67428(67)-10 -11 m³-s -2 -kg -1 , or N-m²-kg -2 ,</p><p>in 2010 the value was revised to:</p><p><i>G</i> = 6.67384(80)-10 -11 m³-s -2 -kg -1 , or N-m²-kg -2 .</p><p>In October 2010, an article [4] was published in the journal Physical Review Letters, suggesting a revised value of 6.67234(14) for <i>G</i>. This value is three standard deviations lower than the value of <i>G</i> recommended by the Committee on Data for Science and Technology (CDST) in 2008. However, it is in line with an earlier value reported by the Committee on Data for Science and Technology (CODATA) in 1986. The difference in the value of <i>G</i> between 1986 and 2008 can be attributed to research conducted on the inelasticity of suspension strands in torsion weights [5].</p><h2>Measurement’s Historical Background</h2><p>The law of universal gravitation, as recorded in modern times, did not explicitly include the gravitational constant until the early 19th century. It was not until the transition to a unified metric system of measures that the gravitational constant was introduced into the law of universal gravitation. This introduction is attributed to the French physicist Poisson in his “Treatise on Mechanics” (1809), as no earlier works that mention the gravitational constant have been identified by historians. In 1798, Henry Cavendish conducted an experiment using torsion weights invented by John Michell to determine the average density of the Earth (Philosophical Transactions 1798). Cavendish compared the pendulum oscillations of a test body under the gravity of known mass balls and under the gravity of the Earth. The numerical value of the gravitational constant was later calculated based on the average density of the Earth. The accuracy of the measured value of G has improved since Cavendish’s time, but his result [6] was already very close to the modern value.</p><h2>Notes</h2><ol><li><b>↑</b> Notations using the letter <i>G</i> are rarely used in the general theory of relativity, as it is usually used to denote the Einstein tensor.</li><li><b>↑</b> By definition, the masses included in this equation are gravitational masses, but there has been no experimental evidence of a discrepancy between the value of gravitational and inert masses of any body. Theoretically, within the framework of modern concepts, they are unlikely to be different. This assumption has been standard since Newton’s time.</li><li><b>↑</b> CODATA Internationally recommended values of the Fundamental Physical Constants. Archived from the original source on August 26, 2011.Checked October 28, 2008.</li><li><b>↑</b>Phys. Rev. Lett. 105 110801 (2010) in arXiv.org</li><li><b>↑</b>Physics News for October 2010</li><li><b>↑</b>Various researchers have provided different findings, ranging from 6.754-10 -11 -11 m²/kg² to (6.6 ± 0.04)-10 -11 m³/(kg-s³) – refer to the Cavendish experiment#Calculated value.</li></ol><h2>References</h2><p>Wikimedia Foundation . 2010 .</p><p>Upon completing a course in physics, students often retain various constants and their meanings. The topic of gravitation and mechanics is no exception. They are frequently unable to explain the significance of the gravitational constant. However, they always acknowledge its presence in the law of universal gravitation.</p><h2>Discovering the Origins of the Gravitational Constant</h2><p>Interestingly enough, Sir Isaac Newton’s extensive body of work does not mention the existence of a specific value for the gravitational constant. It was only in the early 19th century that physicists began to acknowledge its significance. However, this does not imply that it did not exist prior to that time. Rather, scientists had not yet defined it or calculated its precise value.</p><p>Speaking of its value, the gravitational constant is continuously refined due to its decimal nature, which consists of numerous digits after the decimal point, preceded by a zero. Consequently, its exact value is subject to ongoing scientific investigation and refinement.</p><p>What makes this constant particularly intriguing is its minuscule value, which explains why gravitational forces have a negligible effect on small objects. The presence of this small multiplier results in an imperceptible gravitational force.</p><p>In 1788, the physicist G. Cavendish conducted the first experimental measurement of the gravitational constant.</p><p><img loading=](https://dic.academic.ru/dic.nsf/ruwiki/7cdf733b81cd2b83d434160241d6023c.png)
During his experiments, he utilized a slender rod. This rod was suspended by a delicate copper wire and had a length of approximately 2 meters. At the ends of the rod, two identical lead spheres with a diameter of 5 centimeters were affixed. Adjacent to these spheres, larger lead spheres were attached, measuring 20 cm in diameter.
Upon bringing the larger and smaller spheres close to one another, the rod was observed to rotate, indicating their mutual attraction. Through consideration of the known masses, distances, and the measured rotational force, it became possible to accurately determine the value of the gravitational constant.
And it all began with the gravitational pull on objects in motion
If you were to release objects of varying masses into the vacuum of space, they would all experience the same acceleration. This is true as long as they are released from the same height and at the same moment in time. Through careful calculations, scientists have determined that this acceleration is approximately 9.8 m/s 2 , which is the rate at which all objects fall towards the Earth.

The existence of a force that attracts everything to the Earth has been discovered by scientists. This force remains constant regardless of the altitude at which an object is positioned. Whether it is one meter, a kilometer, or hundreds of kilometers away, the object will always be drawn towards the Earth. The question that arises is how the strength of this force is affected by the distance.
It was the English physicist I. Newton who provided an answer to this question.
Firstly, he proposed the hypothesis that the gravitational force is diminishing, with its magnitude being inversely proportional to the square of the distance. Furthermore, this distance must be measured from the planet’s center. Subsequently, he conducted theoretical computations to support his claim.
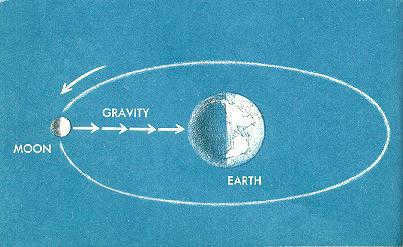
Afterwards, this scientist utilized the astronomical information provided by astronomers concerning the motion of the Moon, Earth’s natural satellite. Newton performed calculations to determine the acceleration at which the Moon orbits around the planet and obtained identical results. This confirmed the validity of his reasoning and enabled him to establish the law of universal gravitation. However, Newton’s formula was still missing the gravitational constant. At this stage, it was crucial to establish the relationship between the variables. And so it was accomplished. The gravitational force diminishes in inverse proportion to the square of the distance from the center of the planet.
Towards the concept of the law of universal gravitation.
Newton continued to contemplate. Considering the fact that the Earth attracts the Moon, it logically follows that it must also be attracted to the Sun. Moreover, this force of attraction must adhere to the principles he had previously described. Subsequently, Newton extended this concept to encompass all celestial bodies within the entire universe. This is why the law is referred to as “universal”.
The forces of universal gravitation between bodies are defined as being directly proportional to the product of their masses and inversely proportional to the square of the distance separating them. Once the coefficient was determined, the formula for the law took on the following form:
This law introduced the following notations:
The formula for the gravitational constant can be derived from this law:
The Significance of the Gravitational Constant
Now it’s time to discuss the specific figures. As scientists continue to refine this value, different numbers have been officially adopted in different years. For instance, based on the data from 2008, the gravitational constant is determined to be 6.6742 x 10 -11 Nˑm 2 /kg 2 . However, after three years, the constant was recalculated, and it is now recognized as 6.6738 x 10 -11 Nˑm 2 /kg 2 . Nevertheless, when solving problems for schoolchildren, it is acceptable to round it up to this value: 6.67 x 10 -11 Nˑm 2 /kg 2 .

What is the significance of this numerical value?
If we plug in specific values into the equation provided for the law of universal gravitation, we obtain an intriguing outcome. In the specific scenario where the masses of the objects are equal to 1 kilogram and they are separated by a distance of 1 meter, the gravitational force is equal to the very number that is recognized as the gravitational constant.
What is the relationship between the gravitational constant and the acceleration of free fall?
When comparing the formulas for gravity and Earth’s law of gravitation, a simple pattern emerges. The gravitational constant, the mass of the Earth, and the square of the distance from the center of the planet combine to form a coefficient that is equal to the acceleration of free fall. This relationship can be expressed in the following formula:
Furthermore, the following notations are used:
Interestingly, the gravitational constant can also be derived from this formula:
If you need to determine the acceleration of free fall at a specific height above the planet’s surface, the following formula will be useful:
Exercises that require knowledge of the gravitational constant
Prerequisite: What is the gravitational acceleration on one of the planets in our solar system, such as Mars? We have information that the planet’s mass is 6.23-10 23 kg and its radius is 3.38-10 6 meters.
Solution: We can utilize the formula originally established for Earth and substitute the given values into it. Consequently, the gravitational acceleration will be the result of multiplying 6.67 x 10 -11 with 6.23 x 10 23, followed by division by the square of 3.38-10 6. The numerator yields a value of 41.55 x 10 12, while the denominator becomes 11.42 x 10 12. The exponents can be simplified, so all that remains is to calculate the quotient of these two numbers to obtain the answer.
Requirement. What action needs to be taken in order to decrease the force of attraction between the objects by a factor of 100?
Resolution. As the mass of the objects cannot be altered, the force can be reduced by increasing the distance between them. A factor of 100 is achieved by squaring 10. Therefore, the distance between them should be increased by 10 times.
The solution: separate them to a distance 10 times greater than the original distance.
All objects in the natural world experience a force of attraction due to their mass. This force, known as gravitational force or force of attraction, is a fundamental property of bodies.
The Law of Universal Gravitation Formula Explained
By knowing the masses of two bodies and the distance between them, we can determine the strength of their mutual attraction using the following formula:
\[ \large \boxed{F = G \cdot \frac{m_1 \cdot m_2}{R^2}} \]
\(F\) (Newtons) is the force with which two spherical bodies are attracted.
\(m_1\) (kilograms) is the mass of the first body.
\(m_2\) (kilograms) is the mass of the second body.
\(R\) (meters) – distance between the centers of the bodies
\(G = 667 \cdot 10^{-11}\) is the gravitational constant.
- The formula allows for the accurate calculation of the attraction between two homogeneous spheres;
- If the bodies are not spherical or homogeneous, the gravitational force is not accurate;
- The greater the distance between the bodies, the smaller the error;
Verbal expression of the universal law of gravitation
The law of gravitation can be described in words as follows:
There is an attractive force between two bodies
that is directly related
to the masses of the bodies
and inversely related
to the square of the distance between them.
The force between two bodies is directly related to the masses of the bodies. This relationship is described by mathematicians as follows:
\[ F \sim m_1 \cdot m_2 \]
In simpler terms, this means that as the masses of the bodies increase, the force of attraction between them also increases.
On the other hand, the force is inversely related to the square of the distance between the bodies. This inverse relationship is represented by a fraction, with the denominator being a value that is inversely proportional to the value on the left side of the equation:
\[ F \sim \frac{1}{d^2} \]
In simple terms, this means that as the distance between the bodies increases, the force of attraction between them decreases.
Definition of the gravitational constant
Physicists commonly refer to the concept of “Physical meaning.” The physical meaning of something is the explanation of what it represents in the context of physics.
Let’s understand the physical meaning of the gravitational constant:
The gravitational constant signifies the strength of attraction between two identical 1 kilogram balls when they are placed 1 meter apart.
\(G \ = 667 \cdot 10^ \left( \text \cdot \frac^2>^2>
ight)\) represents the value of the gravitational constant
As you can observe, this force is incredibly weak, hence it goes unnoticed in our everyday lives.
Direction of Gravitational Force
Let’s draw a straight line connecting the centers of the bodies that are attracting each other. This line represents the direction of the gravitational forces between them. In physics, the term “interaction” is often used to describe the effect of one body on another.
\(F_{\text{large ball}}\) is the force with which a large ball is attracted to a small ball.
\(F_{\text{small ball}}\) is the force with which the small ball is attracted to the big ball.
According to Newton’s third law, we know that the bodies interact with forces of equal magnitude. This means that \(F_{\text{large ball}} = F_{\text{small ball}}\). In other words, the forces are equal.
Physicists often pose a humorous question: “Which object attracts the other more strongly – the Moon to the Earth, or the Earth to the Moon?”. The correct answer is: “They attract each other with the same force.”
Choosing the optimal distance to substitute into a formula
When solving problems involving the center of mass of a body, it is important to determine the appropriate distance to substitute into the formula.
If the body in question is both homogeneous and spherical, the center of mass can be found at the exact center of the ball.
The distance between bodies can then be calculated as the distance between their respective centers of mass.
Let’s consider a few practical examples to better understand this concept:
Example 1. Attraction between a planet and a star
\( R = \left( r_1 + h + r_2
ight) \)
By adding the radii of the balls and the distance between their surfaces, we can calculate the distance between the centers of the bodies. This distance should be substituted into the denominator of the formula.
Example 2. Two spherical bodies are in contact with each other
\( R = \left( r_1 + r_2
ight) \).
To find the distance between the centers of mass of the balls, add up the radii of the balls and substitute the result into the formula instead of R.
Example 3. A tiny object is located on the surface of a celestial body
\( R = r \)
The distance between the objects is equal to the radius of the celestial body. The size of the rock is insignificant compared to the size of the celestial body, so we disregard the size of the rock.
Example 4. A tiny object is situated at a certain distance from the celestial body
\( R = \left( r + h
ight) \)
Add the radius of the celestial body to the distance from the satellite to the surface of the celestial body. The sum is the distance between the objects. The size of the satellite is not taken into account, as it is negligible compared to the size of the celestial body.
Velocity in outer space for the first time
Rotational movement, inward force, and inward acceleration
Acceleration during unrestricted descent
Exclusive IT News
Stay informed and catch up on the most recent news today from Exclusive IT News


(Opens in a new tab)
This particular experiment, known as Torsional Balance Technology, utilized a setup consisting of two dumbbells capable of rotating around a single axis. One of the dumbbells was equipped with two small balls attached to a rod, which was then suspended on delicate fibers. The other dumbbell had a larger weight of 348 pounds (158 kg), balancing out the smaller dumbbell on the opposite side.
By arranging the larger weights alongside the smaller balls, Cavendish observed that the gravitational force exerted by the larger balls attracted the smaller balls, resulting in the twisting of the fibers. This twisting indicated the degree of torsion in the system, which allowed Cavendish to measure the torque, or rotational force. Instead of using the variable “F” in the equation mentioned above, Cavendish utilized this torque value, along with the masses of the weights and their distances, to modify the equation and calculate “J”.
Is it possible for the gravitational constant to vary?
This is a matter of frustration within the scientific community as the precise value of the “Big G” constant is not known to the same level of accuracy as other fundamental constants. For instance, the charge of an electron is known to nine decimal places (1.60217666634 × 10^-19 coulombs), while the gravitational constant can only be measured reliably to five decimal places. Unfortunately, efforts to determine its value more precisely have yielded inconsistent results.
In the 1960s, physicist Robert Dickey and his team embarked on a mission to uncover the secrets of the cosmic microwave background (CMB), a phenomenon famously discovered by Arno Penzias and Robert Wilson in 1964. Additionally, they collaborated with Carl Bruns to develop the standard tensor theory of gravity, a variant of Albert Einstein’s General theory of relativity. In this theory, gravity is represented by a scalar field, which describes a property that can vary at different points in space, similar to a temperature map of the Earth where temperature varies depending on location. This scalar field, denoted as J, can have different values in both space and time, a departure from the prevailing belief that gravity is constant throughout the universe.
Motohiko Yoshimura from Okayama University in Japan has proposed a connection between the theory of scalar gravity and cosmic inflation to explain dark energy. Inflation took place shortly after the birth of the universe and led to a brief yet rapid expansion of space, occurring between 10^-36 to 10^-33 seconds after the universe’s inception. big bang During this period, the universe expanded from a microscopic scale to a macroscopic scale before inexplicably contracting.

(Opens in a new tab)
Dark energy is an enigmatic force responsible for accelerating the expansion of the universe in the present day. Many physicists have pondered whether there could be a connection between these two expansion forces. According to Yoshimura, there is a possible link – both phenomena could be manifestations of a scalar gravitational field that was much more powerful during the early stages of the universe, weakened as the universe expanded, and then regained strength.
However, there have been no significant differences found in the G. in other parts of the universe. For instance, in 2015, the findings of a 21-year investigation on regular pulsars were published. The pulsar PSR J1713 + 0747 was not found in the catalog (Opens in a new tab). Gravity operates differently in comparison to the solar system. There is no Green Bank Observatory and Arecibo Radio Telescope. It is accompanied by PSR J1713+0747, which is located 3,750 light-years away in a binary system with a White Dwarf. This pulsar is widely recognized, and any deviation from the “Big G” would be readily apparent in its orbital dance with the white dwarf and the timing of its pulses.
In a statement (Opens in a new tab), Wei Zhou from the University of British Columbia, who conducted the research on PSR J1713+0747, emphasized the significance of testing the fundamental assumption of the gravitational constant in physics. It is crucial to examine this assumption with objects located in various locations, at different points in time, and in diverse gravitational environments. The observation that we observe gravity in our solar system behaving similarly to how it does in distant star systems helps validate the universality of the gravitational constant.
Examine the laboratory tests conducted by the Eöt-Wash group at the University of Washington to assess the gravitational force (Opens in a new tab).
Explore the attempts made to measure the “big G” and the potential implications of the results (Opens in a new tab).
Table of Contents
Read the article titled “Accurate measurement of the Newtonian gravitational constant” by Xue, Chao, et al. in the National Science Review (2020) (Opens in a new tab).
Find out more about the peculiar state of the gravitational constant in the article published in the Proceedings of the National Academy of Sciences (2022) (Opens in a new tab).
Learn about Henry Cavendish and his contributions to the understanding of gravity (Opens in a new tab) in the Britannica (2022) article.
Stay updated by following Keith Cooper on Twitter (Opens in a new tab), and also connect with us on Twitter (Opens in a new tab) and Facebook (Opens in a new tab).