Scientists find the diameter of the Earth to be of great practical significance. It can be determined by calculating the circumference of the planet along the equator.
The primary characteristics of the Earth
Planet Earth is estimated to be at least 4.5 billion years old. It belongs to the terrestrial group of planets, along with Mercury, Venus, and Mars. Unlike the gas giants (Jupiter, Saturn, Neptune, Uranus), these planets are composed of rocks that cover their surfaces with a thin layer. Among the terrestrial group of planets, Earth is the largest and the fifth largest in the entire solar system.
What sets Earth apart is that it is the only planet known to support life. This can be attributed to:
- The distance from the Sun, which is approximately 150 million kilometers.
- Surface temperature: the average temperature is +13 ° C, with a minimum temperature not exceeding -90 ° C and a maximum temperature of +60 ° C.
- Water, which is essential for life, covers 71% of the Earth’s surface.
- The composition of the atmosphere is as follows: 78% nitrogen, 21% oxygen, and 1% argon.
The Earth surpasses all other planets in the Solar System in terms of physical parameters:
- The mass is approximately 5.9722±0.0006×1024 kg;
- The volume is approximately 1.08321×10¹² km³;
- The density is approximately 5.514×10 g/cm³;
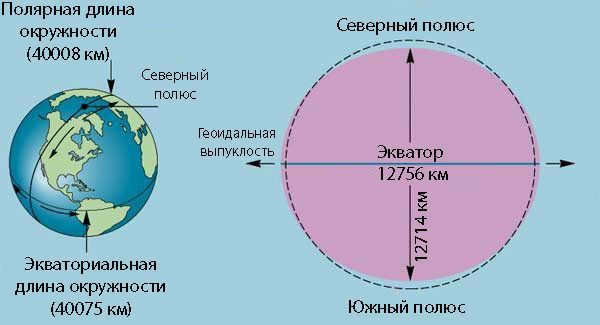
- The circumference at the equator is approximately 40075.16 km, with a diameter of 12756.1 km;
- Between the poles, the parameters are slightly smaller: the circumference is approximately 40008 km and the diameter is 12713.5 km.
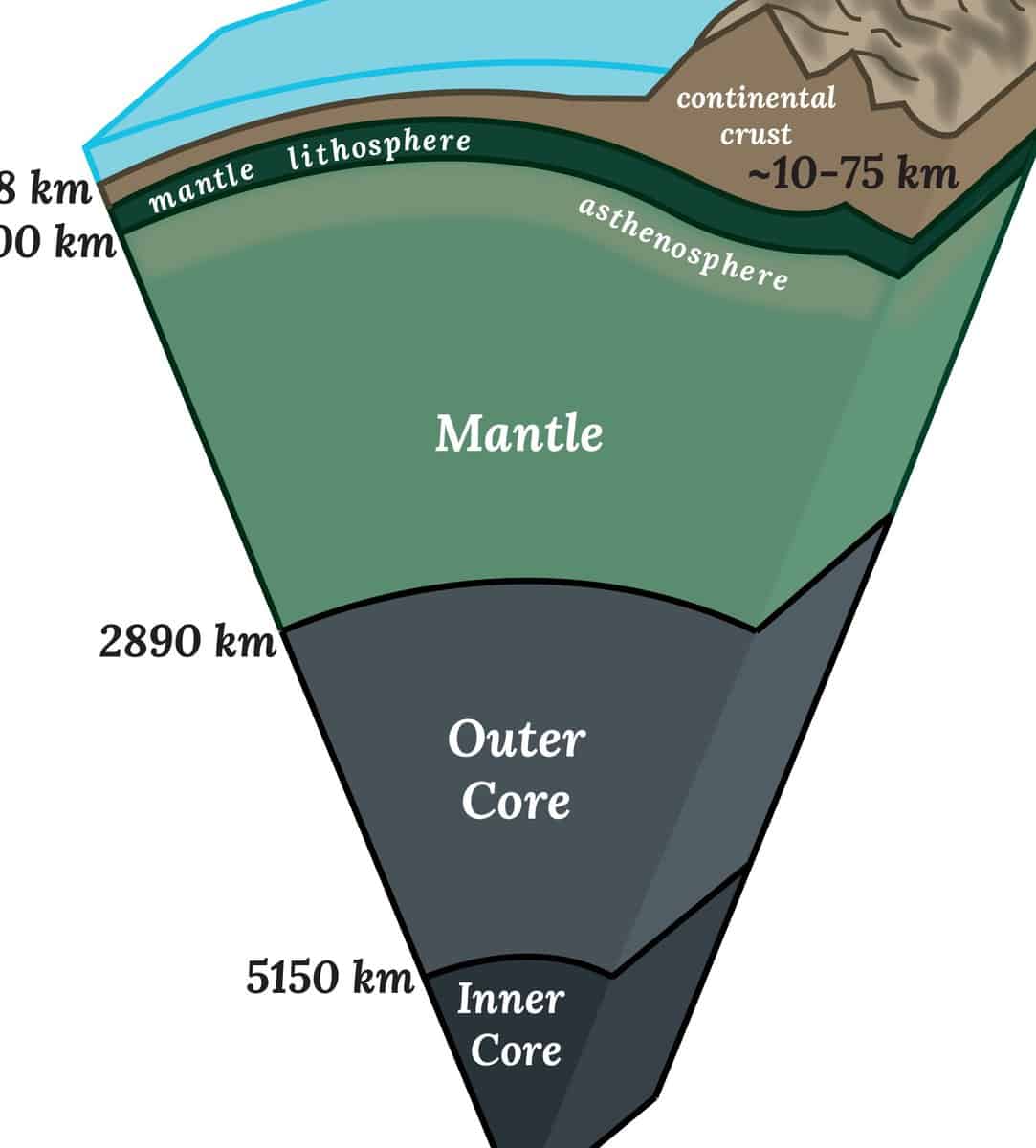
The Earth is the densest planet in the Solar System due to its solid inner core, which occupies about 30% of its volume. It is surrounded by a liquid mantle (70-80% of the volume) and crust (1%).
Formation of the Earth
While commonly referred to as a sphere, the shape of our planet is not accurately described by this term. The topographical features such as ocean trenches and mountain peaks are negligible when considering the overall shape of the Earth. In fact, the difference in elevation between the lowest point, the Mariana Trench, and the highest point, Mount Everest, is a mere 19 kilometers.
Gravity plays a significant role in shaping the Earth. The gravitational force pulls the mass towards the center, causing the celestial body to contract and adopt a spherical form. Additionally, the rotational motion of the Earth generates a centrifugal force, which is most pronounced at the equator. As a result, the equatorial region has the largest circumference and diameter.
What is the purpose of the equator and why is it important?
The equator serves as a reference line perpendicular to the axis of rotation, marking a line around the Earth that is equidistant from the poles. Because of the Earth’s spherical shape, the equator is the longest parallel. Its position relative to the plane of the Earth’s orbit can vary between 22-24.5° due to the gravitational forces of other planets and the Sun.
Along the equator, day and night are equal in length with no deviation. During the equinox, which occurs twice a year, the sun’s rays are directly overhead. On other days, the angle of the sun’s rays is not significantly different, resulting in the equatorial regions receiving a high amount of ultraviolet light. This creates a perpetually summer-like climate with hot and humid air due to constant evaporation.
To perform calculations, it is necessary to divide the planet into parallels and meridians. The equator has a geographic latitude of 0 °, serving as the baseline for all Earth coordinates and dividing it into two equal halves.
Parallels and meridians are utilized to determine the location of objects. They are employed for navigation in the air, on land, and in water. Furthermore, they help differentiate between climatic zones and time zones.
Measuring the Earth’s Circumference Using Geometry
Special instruments and space satellites are typically used to measure the circumference of the earth along the equator. However, it is also possible to obtain these measurements using knowledge of geometry, without the need for complex tools. Ancient Greek scientist Eratosthenes was the first to successfully accomplish this.
Legend has it that travelers informed Eratosthenes that on the summer solstice, they observed that the bottom of the deepest wells were illuminated and objects did not cast shadows. This was because the sun was directly overhead. These observations were made 500 miles south of Alexandria, in Siena. Eratosthenes, who lived in Alexandria, knew that in his hometown, objects did cast shadows and the sun did not appear directly overhead in deep wells.
During the midday of the longest day in summer, Eratosthenes decided to measure the length of the shadow cast by the obelisk in the city, knowing its height. With this information, he was able to calculate the length of an imaginary line connecting the top of the obelisk with the tip of its shadow. By using this data, I was able to determine the angles of the imaginary triangle – 7 degrees. This indicated that Siena was positioned at such a distance from Alexandria.
An angle of 7 degrees is approximately 1/50th of a complete circle, which always measures 360 degrees. The astronomer then continued his calculations. He multiplied the distance to Siena by 50. The resulting measurement of the Earth’s circumference was 25,000 miles. Modern research has shown that the scientist was not far off: the equatorial circumference of the planet is actually 24,894 miles or 40,075 kilometers.
The inaccuracy of Eratosthenes’ calculation is not caused by the simplicity of the computations he employed. This technique is precise and is still employed nowadays, albeit with more sophisticated instruments. The scientist was unaware of the precise distance between the cities, which was determined in those times based on the number of days it took for caravans to travel between them.
The second cause of the imprecision is that Alexandria and Siena are situated on different meridians. Presently, the circumference between objects on the same meridian is calculated.
Calculating the circumference and diameter
When you know the circumference, it is simple to calculate the radius and diameter of the sphere. The following formulas can be used: d=l/π; r=½*π. The variables stand for:
- d represents the diameter. It connects opposite sides of the circle and passes through the center.
- l is the length of the circle. It is a line that is equidistant from the center.
- r is the radius. This is the name given to the line drawn from the center to any point on the circle.
- π is a number equal to 3.14. It is an infinite number, so the more digits after the decimal point, the more precise the calculation.
It is not necessary to use both formulas. The diameter and radius are interconnected. Calculate one value, and then determine the other: the diameter is twice the radius, and vice versa.
How long does it take to circumnavigate the planet on foot?
In order to determine how long it would take to go around the Earth on foot, we need to calculate the length of the equatorial circle in kilometers. Using this value and the estimated speed of a pedestrian, we can then determine the time it would take. The formula used for this calculation is: t=S:V. In this formula, “S” represents the distance to be covered and “V” represents the speed of the pedestrian.
If we were to walk the Earth along the equator, we would need to cover a distance of 40,075 kilometers. The average speed of a pedestrian is typically around 6 kilometers per hour. By substituting these values into the formula, we find that it would take approximately 6,679 hours to complete the journey. When converted to days, this equates to 278 days.
It’s important to note that these calculations are purely hypothetical, as the equator only passes through certain countries and islands, such as America, Africa, and Indonesian islands. The rest of the journey would be through the oceans, including the Atlantic, Indian, and Pacific oceans.
Fascinating information about the Earth’s equator
The region surrounding the equator is known for its warm and humid climate. It is home to an incredibly diverse range of plant and animal species, with dense forests that are often impenetrable. The summer season lasts all year round, with average temperatures ranging from +25 to +30°C. The night temperatures are not significantly different from the daytime, as the earth continues to be warmed by the sun. Rainfall is also a common occurrence, happening almost every day.
This unique climate attracts tourists from around the world, although not all countries have the same conditions. The Maldives, Ecuador, Brazil, and Kenya are among the most popular destinations for travelers seeking to experience the equatorial climate.
In addition to the climate, equatorial countries also offer a variety of geographical attractions:
- The equator passes through a total of 33 islands, with 17 of them falling within the territory of Indonesia. Some of these islands are not located in the ocean, but rather in a lake on the Indonesian island of Kalimantan (2 islands), at the mouth of the Amazon River (9 islands), and on the African Lake Victoria (5 islands).
- There are a total of 14 countries that are situated along the equator. One of these countries is Ecuador, which is named after the equator that runs through it. It is quite a feat for any traveler to have crossed all of these countries while staying on the equator.
- With the exception of Gabon and Somalia, almost all equatorial countries have erected memorial signs to commemorate the zero parallel. Some of the most stunning signs can be found in Brazil and Ecuador.
- Within the Galapagos archipelago, there is an active volcano called Wolf that straddles both sides of the equator.
- The Cayambe volcano, located not far from Quito (the capital of Ecuador), stands tall and majestic with its snow-white appearance. With an impressive altitude of 4690 meters, its slopes are adorned with a perpetually glistening layer of ice.
- A fascinating natural wonder, the Congo River in Africa holds the unique distinction of crossing the equator not once, but twice.
- Man has harnessed the extraordinary physical characteristics of the zero parallel to his advantage. In this region, the Earth rotates at a remarkable speed of 1.4 times faster than the speed of sound. This exceptional velocity makes it an ideal launch site for space satellites, as they are instantly propelled to supersonic speeds, resulting in a significant 10% fuel savings. Moreover, geostationary communication satellites orbit above the equator, ensuring that signals reach the Earth more rapidly than in any other area.
Exploring the Earth: Examining its Form, Dimensions, and Geodesy

The Earth, situated at an average distance of 149,597,890 kilometers from the Sun, is the third planet in the solar system and possesses several distinctive features. It came into existence approximately 4.5-4.6 billion years ago and stands out as the only known planet capable of sustaining life. The planet’s ability to support life can be attributed to various factors, including its atmospheric composition and physical attributes such as the abundance of water, which covers around 70.8% of the Earth’s surface, providing a conducive environment for life forms to flourish.
In addition, the Earth holds a unique position as the largest member among the terrestrial group of planets (Mercury, Venus, Earth, and Mars). Unlike the gas giants (Jupiter, Saturn, Neptune, and Uranus), the Earth consists of a relatively thin layer of rock. When considering factors such as mass, density, and diameter, the Earth ranks as the fifth largest planet in the entirety of the solar system.
Earth’s Dimensions: Mass, Volume, Circumference, and Diameter
With an estimated mass of 5.9722±0.0006×10^24 kg, Earth is the largest planet in the terrestrial group. Its volume, measured at 1.08321×10^12 km^3, is also the largest among these planets.
Furthermore, Earth stands out as the densest planet in the terrestrial group due to its composition of crust, mantle, and core. The Earth’s crust is the thinnest layer, while the mantle occupies 84% of the planet’s volume and extends 2900 km beneath the surface. The core, which surrounds a solid and dense inner core, contributes to Earth’s high density. Among the Earth-group planets, it is the only one with a liquid outer core.
Earth has an average density of 5.514×10 g/cm^3. In comparison, Mars, the smallest of the Earth-like planets in the solar system, has only about 70% of Earth’s density.
The Earth’s Shape
The Earth is not a perfect sphere, but rather a flattened spheroid or ellipsoid, which is why its circumference and diameter differ. The poles of the planet are slightly flattened, causing a bulge at the equator and resulting in a larger circumference and diameter.
The equatorial bulge of the Earth measures 42.72 km and is a result of the planet’s rotation and gravity. Gravity itself causes celestial bodies, including planets, to contract and take on a spherical shape. This occurs because gravity pulls the entire mass of an object towards its center of gravity, which in the case of the Earth is its core.
When the planet spins, the centrifugal force distorts the sphere. This force is responsible for pushing objects away from the center of gravity. As the Earth rotates, the strongest centrifugal force is at the equator, resulting in a small bulge that extends outward. This leads to an increase in both the circumference and diameter of the equatorial region.
Local topography also has an impact on the shape of the Earth, although its effect is minimal when considered on a global scale. The Earth’s topography varies greatly in different regions, with Mount Everest standing as the highest peak above sea level at 8,848 meters and the Mariana Trench as the deepest point below sea level at 10,994±40 meters. However, the difference between these two points is only about 19 km, which is relatively insignificant when viewed from a planetary perspective. When taking into account the equatorial bulge, the highest point on Earth and the point farthest from the Earth’s center is the summit of the Chimborazo volcano in Ecuador, which reaches an elevation of 6,267 meters and is located near the equator.
Geodesy and its Importance in Earth Measurement
Geodesy, a scientific discipline focused on the precise measurement and characterization of the Earth’s size and shape through extensive surveys and complex mathematical calculations, plays a crucial role in the comprehensive study of our planet.
Since ancient times, geodesy has held significant significance as early scholars and thinkers embarked on determining the true nature of the Earth. Aristotle, often regarded as the pioneer of geodesy, was the first to venture into calculating the Earth’s size, making him an early geodesist. Following his footsteps, the Greek philosopher Eratosthenes estimated the Earth’s circumference to be 40,233 kilometers, a measurement that remains remarkably close to the accepted value today.
To investigate the Earth and utilize geodesy, scientists frequently rely on the ellipsoid, geoid, and reference ellipsoid. The ellipsoid is a conceptual mathematical framework that presents a streamlined, simplified depiction of the Earth’s exterior. It is utilized to calculate distances on the surface without factoring in variables like changes in altitude and topographical features. Acknowledging the complexities of the Earth’s exterior, surveyors employ a geoid, a representation of the planet that is created using the average sea level worldwide, thus considering variations in elevation.
Calculating the Earth’s Circumference 2,500 Years Ago: The Largest Diameter and the Time it Takes to Walk Around
The measurement of the Earth’s diameter holds great significance for scientists. It enables the calculation of our planet’s area and the distance to its core. Additionally, it aids in cartography and space exploration. Let’s delve into the methods used to determine these parameters and the values they yield.

Essential Characteristics of Earth
One of the distinctive features that sets Earth apart from other planets in the solar system is its ability to sustain life. Here are the key parameters of our planet:
- Distance from the Sun in kilometers: approximately 150 million. This distance is optimal for the development and continuation of life. If the Earth’s orbit were a few million kilometers closer or farther from the Sun, the conditions for the evolution of life would be significantly compromised.
- The Earth takes 365 days, 5 hours, 48 minutes, and 46 seconds to complete one revolution around the Sun. It also takes 23 hours, 46 minutes, and 4 seconds to complete a revolution around its axis. Over the course of 100 years, the speed of these rotations decreases by 0.017 seconds. If this trend continues, it would take approximately 140 million years for the length of a day to increase by one hour.
- The Earth’s axis of rotation is tilted at an angle of slightly over 23 degrees relative to its orbital plane. This tilt is responsible for the seasonal variations in climate and the distinct change of seasons. If the axis of rotation were inclined at a slightly different angle, the Earth would experience less favorable climatic conditions and larger areas of the surface would be covered in glaciers.
- The average temperature on Earth is approximately 15°C.
- Water covers approximately 71% of the Earth’s total surface area, with a mass of 1460 million billion tons. In comparison, the atmosphere is much lighter, weighing just over 5 quadrillion tons.
- The atmosphere is composed of 21% oxygen, while the majority of it, 78%, is made up of nitrogen, which is biologically inert.
- The Earth has a mass of approximately 6∙10 24 kilograms.
- The volume of the planet is 1.08∙10 12 cubic kilometers.
- The Earth’s surface area is 510 million square kilometers.
- The density of the Earth is 5.5 g/cc.
- At the equator, the circumference of the Earth is 40075 kilometers, while at the poles, it is 40008 kilometers.
- The diameter of the Earth at the equator is 12756 km, and at the poles, it is 12713 km.
- The average radius of the Earth is 6371 km, with the center of the core located at this distance from the surface. The equatorial radius of our planet measures at 6378 km, while the distance to the center of the Earth at the poles is approximately 6356.5 km.
- When it comes to celestial bodies, the Moon takes the prize for being the closest one to us. It maintains an average distance of about 384 thousand kilometers from the Earth.
The configuration of the planet
When inquired about the configuration of the Earth, the majority of individuals will respond that it is spherical. However, this response would be incorrect. The planet is influenced by gravitational forces, with its enormous mass gravitating towards the core, resulting in a continuous compression. The most powerful centrifugal force, which arises from the Earth’s rotation on its own axis, is experienced at the equator.
The Earth can be described as an “irregular sphere”. The compression of the planet is responsible for the equatorial diameter being slightly larger than at the poles. Scientists classify the shape of our planet as being close to a “flattened ellipsoid”.
Interestingly, due to the disregard of the compression at the poles, the meter standard from 1795 was 200 microns shorter.
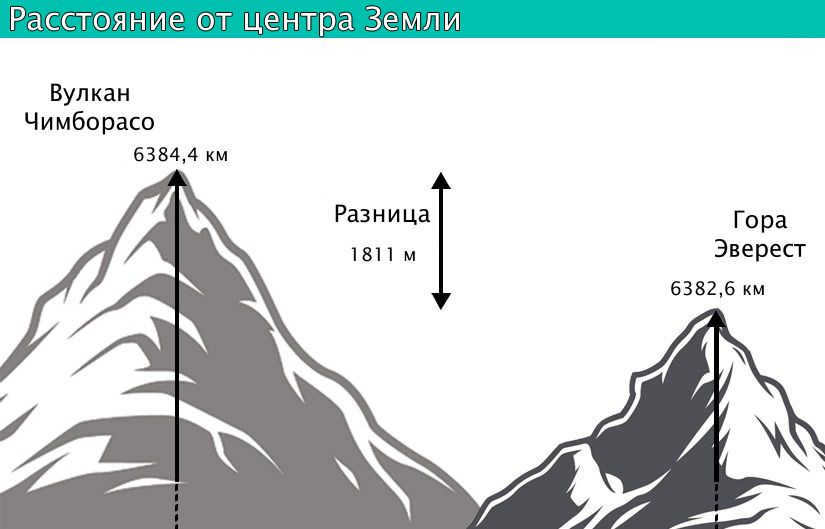
Difference in distance between the center of the Earth and the highest points of Chimborazo volcano and Mount Everest.
What is the purpose of the equator and what does it represent?
The equator is a line that runs perpendicular to the Earth’s axis, dividing the Earth’s surface into two equal halves and located equidistant from the North and South Poles.
Along the entire length of the equator, the duration of the day and night is equal. However, due to atmospheric refraction, the day length is slightly longer by a few minutes. On the days of the equinoxes, which occur twice a year, the Sun is positioned directly overhead at the zenith, resulting in perpendicular rays to the Earth’s surface. The latitude at the equator is 0°.
The latitude of a geographic feature is determined by its position relative to the equator. Any point located to the south of the equator is said to have a southern latitude, while points to the north of the equator have a northern latitude.
Measuring the Earth’s Circumference: A Historical Perspective
The Earth’s size has been a subject of scientific inquiry for centuries. Modern technology, such as advanced instruments and satellites, allows for precise measurements of the Earth’s circumference. However, before these innovations, ancient mathematicians devised methods to estimate its size. In the 18th century, scientists P. Meschen, A.M. Lejeandre, and C. Cassini employed triangulation as a means of measurement.
Imagine the challenge of measuring the distance between two points separated by hundreds of kilometers. To overcome this, a network of reference points was constructed on the terrain, using triangles as the building blocks. These triangles were formed by connecting high-altitude locations, and from each vertex, imaginary pyramids were extended towards nearby points of interest.
The fictitious characters ought to be handy for arranging an angle gauge and determining the measurements of the angles. In one of the triangles, a side is measured as it extends along the level ground. This side will serve as the reference line.
The most straightforward method for calculating the circumference of the Earth is to multiply the number of kilometers in one degree by 360.
The process of measuring a circle starts with a triangle serving as the foundation. By examining the sides and angles of this shape, the measurements for the other sides can be determined. One of these sides also acts as the side of the adjacent triangle, which then becomes the baseline for calculating the sides of another triangle. Through mathematical calculations, the parameters of the final triangle can be found, leading to the determination of the meridian arc. By having longer meridian arcs, it becomes easier to calculate the desired value – the radius of our planet.
Once the length of the meridian arc is known, it is not challenging to calculate the length of one degree. This method forms the foundation of geodesy.
Calculating the circumference and diameter of the Earth is a straightforward task. You can use the following formulas: d=l/π; r=½π. Each letter represents:
- d – diameter;
- l – the length of the circle;
- r – radius (a line drawn from the center to any point on the circle);
- π is a constant approximately equal to 3.14 and represents the ratio of the circumference of the circle to its diameter.
Calculating the Earth’s Circumference in Ancient Times
Ancient Greece had knowledge of the Earth’s circumference thanks to the calculations of Eratosthenes, a Greek mathematician, astronomer, and geographer. Eratosthenes discovered that on June 21, the day of the summer solstice, in Siena, which was located roughly five hundred miles from Alexandria, there was no shadow at noon and the bottom of wells were illuminated. This indicated that the sun was directly overhead in Siena, while in Alexandria, no such phenomenon occurred.
Using the height of the city obelisk and measuring its shadow at noon on the summer solstice, Eratosthenes determined that there was a 7-degree difference in latitude between Alexandria and Siena.
The astronomer conducted additional calculations. 7° corresponds to approximately 1/50th of a circle which is equivalent to 360°. By multiplying the distance between Siena and Alexandria by 50, the mathematician arrived at the figure of 25,000. This represents the total number of miles comprising the Earth’s circumference.
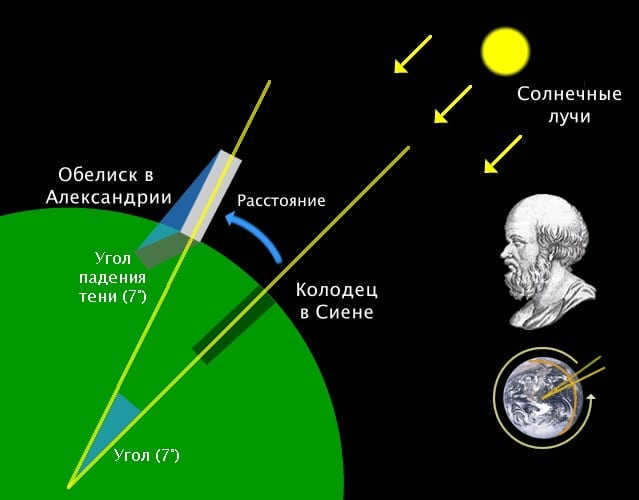
Eratosthenes’ estimation of the Earth’s circumference
The measurement of the Earth’s circumference carried out by Eratosthenes was slightly less than the actual value. This discrepancy was not due to inaccurate calculations: Eratosthenes’ method of determining the Earth’s circumference was quite precise. During Eratosthenes’ time, the exact distance between the two cities was unknown. Additionally, the scientist did not account for the fact that the two cities are located on different meridians.
In the medieval period, the church prohibited any mention of such research. It was only in the 16th century, through Ferdinand Magellan’s circumnavigation, that it was confirmed that the Earth is indeed spherical and its circumference is approximately 40,000 kilometers.
What is the estimated time it would take to walk around the Earth?
By knowing the length of the Earth’s circumference around the equator, we can calculate the estimated time it would take to walk around it. Assuming the average walking speed of 6 kilometers per hour, we can use the formula t = S / V to determine that it would take approximately 6700 hours, or 278 days.

This is the amount of time it would take to circumnavigate the Earth on foot without stopping. Assuming that our hypothetical pedestrian walks for 6 hours per day, it would take them approximately 1110 days, or over 3 years, to complete such a journey.
Fascinating Facts about the Earth’s Equator
The equator experiences a hot and humid climate throughout the year. The forests of the Amazon, equatorial Africa, and Indonesia are home to a diverse range of plant and animal species. During the daytime, temperatures range between 25 and 30 degrees Celsius. Even at night, the temperature remains relatively warm as the Earth’s surface retains heat from the sun’s rays.
However, the equator is also intriguing from a geographical standpoint:
- It passes through more than 30 islands;
- It crosses 14 countries;
- The country of Ecuador is named after the equator;
- Most states located along the equator have erected monuments and memorials to commemorate the zero parallel.
- Not far from Quito, there lies the Cayambe volcano, towering at approximately 4.7 km above sea level, with its peak covered in eternal ice. This is quite remarkable considering the constant heat that characterizes the equatorial climate.
- The Congo River, which passes through the heart of the African continent, intersects the zero parallel twice.
- Due to the Earth’s rapid orbit in this region, it serves as the ideal location for satellite launches, as they can achieve faster speeds.
The size of the Earth is a crucial parameter in the field of astronomy and holds significant practical importance. It allows for the determination of the Earth’s diameter and radius through simple mathematical calculations.

During this class, students will be introduced to the concept of the Earth’s form and dimensions, as well as gain an understanding of the Earth’s daily and yearly rotation.
Currently, you do not have the capability to view or distribute the instructional video
In order to gain access to this and other video lessons within the package, you will need to include it in your individual account.
Obtain extraordinary functionalities

Outline of the Lesson on the Shape, Size, and Movements of the Earth
The Earth’s shape is undisputed – it is a sphere. As early as the 6th century B.C., Pythagoras believed in the round shape of the Earth. Aristotle later proved this by observing that the Earth’s shadow during lunar eclipses is always round. Around 100 years after Aristotle, Eratosthenes measured the length of the Earth’s meridian and calculated its radius. However, it was the English physicist Newton who first demonstrated that the Earth’s shape is not a perfect sphere.
In the 17th century, Isaac Newton used complex calculations to determine that the Earth’s shape is indeed close to being spherical, but it is slightly flattened at the poles. This shape is known as an ellipsoid.
Our planet is in constant motion as it travels through space. However, the Earth’s movement is not readily apparent to us. The Earth is so strongly bound to the air, oceans, and land that they move along with it. In fact, the Earth is simultaneously making two distinct movements. The first is the rotation of the Earth on its axis, also known as diurnal or axial movement. This rotation causes the Earth to turn from one side to the other, facing the Sun at different times. It takes approximately 23 hours, 56 minutes, and 4 seconds (rounded up to 24 hours) for the Earth to complete one full rotation on its axis, which we refer to as a day. This daily rotation governs the cycle of waking and sleeping for all living beings on our planet.
Because of the Earth’s rotation around its axis, the time of day varies in different parts of the world. To make things more convenient, time zones were created. The Earth’s surface was divided into 24 zones based on meridians, with each zone covering 15 degrees of longitude. The time within a specific time zone is called zone time. There is a one-hour difference between adjacent time zones. The Prime Meridian, which runs through Greenwich in Great Britain, is the reference point for counting time zones. Time zones increase as you move eastward and decrease as you move westward from the Prime Meridian. For example, if Greenwich is 12 hours, then the time in the first zone to the east is 13 hours and the time in the first zone to the west is 11 hours. The 12th time zone marks the start of a new day. This means that when a new day begins in the Far East, the previous day is still ongoing in the Western Hemisphere. In 2011, a federal law was signed in our country to establish nine time zones in Russia. The boundaries of these zones are determined by the borders of the republics, territories, and regions of the Russian Federation. Each time zone follows the same time. In the same year, Russia decided to stop observing the transition to winter time.
The Earth’s movement around the Sun is known as the second motion. It is also referred to as annual or orbital motion.
The period of time in which the Earth completes a full revolution around the Sun is known as a year. A year consists of 365 days, 6 hours, 9 minutes, and 10 seconds. Over the course of four years, these extra 6 hours, 9 minutes, and 10 seconds add up to an additional twenty-four hours. This is why every four years, in the month of February (which is the shortest month of the year), an extra day is added, making it 29 days instead of the usual 28. This type of year is called a leap year and consists of 366 days instead of 365.
The Earth’s orbit is the path that the Earth follows as it travels around the Sun.
The change of seasons is determined by the rotation of the Earth around the Sun and its tilt. This rotation and tilt cause each pole to be “exposed” to the flow of rays at different times. As a result, the Northern Hemisphere receives more sunlight than the Southern Hemisphere for half of the year, leading to summer. After six months, the Earth moves to the other side of its orbit, bringing summer to the Southern Hemisphere and causing fall in the Northern Hemisphere. The lack of life-giving solar heat in the Northern Hemisphere then gives way to winter.
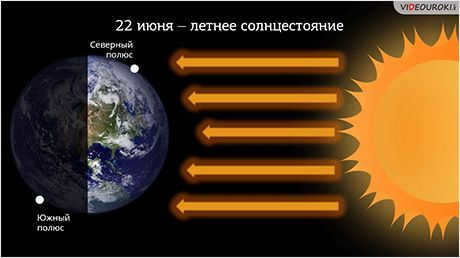
In the Northern Hemisphere, the summer solstice occurs on June 22, which marks the longest day of the year. Conversely, the winter solstice takes place on December 22, representing the shortest day of the year. These solstices signify the peak of summer and the depths of winter. During the summer solstice, the North Pole experiences a phenomenon known as the polar day, where the Sun remains fully visible for a continuous period of six months. This occurs due to the Earth’s rotation on its axis. As a result, the Sun never sets below the horizon line during this time, creating a perpetual daylight. However, this polar day eventually transitions into the polar night, where the Sun remains below the horizon for an extended period of time.

December 22 marks the moment when the South Pole is completely bathed in sunlight. This occurrence coincides with the summer season in the Southern Hemisphere, while the Northern Hemisphere experiences winter. At the South Pole, this day is known as the polar day, while at the North Pole it is referred to as the polar night.

March 21 and September 23 mark the occasions when the Earth’s poles experience equal amounts of sunlight. During these times, the sun is visible at the horizon at both the North and South poles. This phenomenon results in an equal length of day and night across the entire planet. As a result, these dates are referred to as the vernal and autumnal equinoxes.

Polar circles are the conditional lines that mark the beginning of the polar day (or night). In the Arctic Circle on the summer solstice (June 22), the sun almost touches the horizon line at midnight but does not set. This marks the start of a polar day that lasts for 24 hours. At noon on this day, the sun is directly overhead on another imaginary line known as the Northern Tropic. The word “tropicos” in Greek means “turning,” which is why these lines are called tropics. They represent the path where the sun appears to “turn” from one tropic to another.
Ancient Greece was the first to identify the polar circles and the tropics. At that time, it was already understood that the area between the tropics would experience extreme heat, thus creating a hot belt on Earth. This particular belt receives ample heat from the sun’s rays, resulting in warm temperatures year-round with minimal fluctuations.
Outside the polar circles, where the sun appears low in the sky and can be absent for up to half a year, cold belts are found. Due to the sun’s low position, the Earth’s surface in these regions is not significantly heated even during the summer months.
Between the polar circles and the tropics, there are two temperate belts. In these northern and southern temperate belts, there is a noticeable change in seasons.
Summer is the warmest season for two primary reasons. Firstly, summer experiences the longest days of the year. As a result, the Earth’s surface is exposed to the Sun’s rays for a more extended period of time. Secondly, during summer, the Sun is positioned higher in the sky compared to other seasons. Consequently, the angle at which the sun’s rays fall on the Earth’s surface is greater than during fall or winter.
The Earth is in a state of rotation. However, not all points on its surface rotate in the same manner. To illustrate this, you can conduct a simple experiment: take a piece of paper and pierce it with a pencil, then spin the paper around the pencil. While the paper rotates, the pencil remains stationary (as long as you hold it firmly). This indicates that the point where the pencil intersects with the paper remains still. However, everything else rotates around the axis passing through the pencil and this point. The same principle applies to the rotation of the Earth.
The ball is in a state of rotation, but the areas where its surface intersects with the axis of rotation remain stationary. These specific areas are known as poles.
On the Earth’s surface, there are two distinct points that do not partake in the axial rotation – these points are referred to as the poles: the North Pole and the South Pole. What do we understand about these locations? The North Pole is essentially an icy ocean surrounded by continents. In contrast, the South Pole is a continent encircled by oceans.
An interesting fact to note is that the South Pole experiences much colder temperatures compared to the North Pole. In Antarctica (the South Pole), the temperature is so frigid that certain areas on the continent never witness the melting of snow. The average yearly temperature in this region plummets to -58 degrees Celsius during winter, with the highest temperature ever recorded being -12.3 degrees Celsius.
On the contrary, during winter, the Arctic region (North Pole) experiences an average annual temperature of -43 degrees Celsius, while in summer it’s around 0 degrees Celsius.
Now consider this: how many straight lines can be drawn from the North Pole to the South Pole that would always remain equidistant from them? The answer is clear – only one such line exists, and that is the Earth’s axis of rotation. The Earth’s axis is inclined, with a tilt angle of 23.5 degrees in relation to the ecliptic plane. This tilt is accurately depicted on a globe, where instead of an imaginary axis, a metal axis is tilted.
Let’s take another look at the world map. Can you spot the bold line running down the center of the map? It is equidistant from both the North and South poles, effectively splitting the planet in two. This line is known as the equator. The equator serves as the boundary between the Northern and Southern hemispheres of the globe.

At the moment, it is not possible for you to view or share the video tutorial with your students
In order to access this and other video tutorials in the package, you will need to add it to your personal account.
Unlock amazing functionalities


Outline of the Lesson on the Shape, Size, and Movements of the Earth
This lesson will cover the shape and size of the Earth, as well as its daily and yearly rotations. Let’s begin.
Space photographs provide undeniable evidence of the Earth’s spherical shape in modern times. However, it took humanity thousands of years to arrive at this conclusion. Ideas about the Earth’s shape and size have been developed over millennia.
Pythagoras, in the 6th century BC, held the belief that the Earth possessed a rounded shape. This notion was later proven by Aristotle, who pointed to the fact that the Earth’s shadow during lunar eclipses always takes on a round form. Another 100 years down the line, Eratosthenes managed to ascertain the length of the Earth’s meridian and calculate the Earth’s radius.
Nonetheless, it was only during the Middle Ages that the hypothesis of the Earth’s spherical nature was conclusively confirmed, coinciding with the advent of Europe’s initial seafarers embarking on oceanic voyages.
In the 17th century, Isaac Newton utilized intricate calculations to determine that the Earth’s shape is indeed close to that of a sphere, albeit not a perfect sphere. In reality, our planet is somewhat flattened at the poles.
Over time, there have been multiple revisions to our understanding of the Earth’s shape. It wasn’t until the 20th century that we were able to accurately determine its shape using instruments on artificial satellites. We now know that the Earth is not a perfect sphere; it is slightly flattened at the poles and elongated towards the North Pole. This unique shape is referred to as a geoid.

A geoid is a curved, enclosed surface that closely aligns with the calm surface of water in the seas and oceans. It is also perpendicular to the gravitational force at any given point. The geoid can be approximated as an ellipsoid with a compression ratio of 1: 298.2.
The term “geoid” was coined in 1873 by Johann Listing, a German physicist. The compression at the poles is a result of the Earth’s rotation around its axis.
It is well-known that the Earth’s formation was influenced by two forces: the mutual attraction of its particles and the centrifugal force caused by its rotation. This is why the shape of the Earth is such: the faster it rotates, the more it becomes flattened at the poles.
When you compare the Earth to the rest of the planets in the solar system, you’ll find that our planet ranks as the fifth largest out of the eight planets.
What is the measurement in kilometers for the Earth’s radius? In your mathematics course, you are familiar with the concept of a radius. The radius of the Earth refers to the distance from its center to its surface. Due to the Earth’s oblate shape, it is customary to specify two different radii: equatorial and polar. The equatorial radius represents the distance from the planet’s center to the equator, while the polar radius represents the distance from the planet’s center to its pole. These two values vary slightly. The equatorial radius measures 6378 kilometers, whereas the polar radius measures 6356 kilometers. The discrepancy between the two is merely 22 kilometers. Calculating the average radius of the Earth is not a complicated task. By adding the equatorial radius and the polar radius together and dividing the sum by 2, we arrive at a value of 6,367 kilometers. Additionally, the Earth’s diameter measures 12,734 kilometers.
The mass of the Earth was determined through Henry Cavendish’s experiments in 1798, which utilized the law of universal gravitation. The Earth’s mass was calculated to be 5.9*10^24 kg.
With an approximate surface area of 510 million km^2, the Earth consists of 149 million km^2 (or approximately 29% of its total area) of land. This fact suggests that our planet could be more accurately referred to as “Ocean” rather than “Earth.”
Similar to other celestial bodies within the solar system, the Earth undergoes two primary movements: rotation on its own axis and orbit around the Sun. These consistent motions have served as the foundation for timekeeping and the development of calendars throughout ancient history.

The planet Earth spins on its axis in a counterclockwise direction (when observed from the North Pole) as it completes a full rotation every 24 hours, specifically in 23 hours 56 minutes and 4 seconds. This daily rotation establishes the natural cycle of waking and sleeping for all living organisms on our planet.
Because of the Earth’s rotation on its axis, the timing of day varies across different regions of the world. In order to simplify things, time zones were established by dividing the Earth’s surface into 24 zones based on every 15 degrees of longitude. The time within each time zone is referred to as zone time. There is a one-hour difference between adjacent time zones. The Greenwich meridian, which runs through Greenwich (a city near London, Great Britain), is considered the reference point for counting time zones.

The time zones are counted to the east from this meridian. As you travel eastward, the time zone increases, while moving westward decreases it. If Greenwich is 12 hours, then in the first zone to the east of Greenwich it is 13 hours, and in the first zone to the west it is 11 hours. The 12th time zone marks the start of a new day. Therefore, when a new day begins in the Far East, the previous day is still ongoing in the Western Hemisphere.
The Earth’s second movement is its orbit around the Sun, also known as the annual or orbital movement.
The period of time in which the Earth completes a full orbit around the Sun is known as a year. A year consists of 365 days, 6 hours, 9 minutes, and 10 seconds. Over the course of four years, these additional 6 hours, 9 minutes, and 10 seconds accumulate to make an extra twenty-four hours. This is why every four years in February (the shortest month of the year), there is an additional day: instead of having 28 days, February has 29 days. Therefore, a leap year is defined as a year with 366 days instead of the usual 365 days.
The Earth does not move around the Sun in a perfectly circular orbit. Instead, it follows an elliptical path, with the average distance from the Earth to the Sun being about 150 million kilometers. However, this distance can vary by up to 5 million kilometers, forming a small oval shape. The point in Earth’s orbit that is closest to the Sun is known as Perihelion, and it occurs in early January. On the other hand, the point in Earth’s orbit that is farthest from the Sun is called Aphelion, and it occurs in early July.
Now, let’s delve into this topic in more depth.
June 22 marks the longest day of the year in the Northern Hemisphere, known as the summer solstice, while December 22 marks the shortest day, known as the winter solstice. During the summer solstice, the North Pole experiences a phenomenon called the polar day, where the sun remains above the horizon for the entire day due to the Earth’s rotation. This polar day lasts for six months, resulting in continuous daylight. However, as the Earth continues to rotate, the polar day eventually transitions into the polar night.
Conversely, on December 22, the South Pole experiences a polar day, with the sun remaining above the horizon throughout the day. This occurs while the Northern Hemisphere is in winter, experiencing the polar night at the North Pole.
Both poles of the Earth experience equal illumination on March 21 and September 23. At these times, the sun is visible at the horizon at both poles. This results in an equal amount of daylight and darkness throughout the planet. These dates are commonly referred to as the vernal and autumnal equinoxes.
The polar circles mark the boundaries where the polar day or night begins. During the summer solstice on June 22 in the Arctic Circle, the sun’s disk comes very close to the horizon at midnight but does not fully set. This creates a polar day that lasts for 24 hours. Additionally, on this day, the sun is directly overhead on another imaginary line known as the Northern Tropic. The word “tropic” comes from the Greek word “tropikos,” meaning “turning.” This name reflects the sun’s apparent “turning” as it moves from one tropic to the other.
Ancient Greece is where the polar circles and the tropics were initially designated.
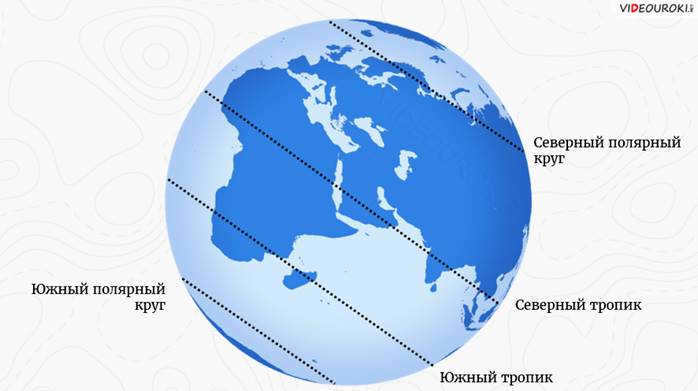
At that time, it was assumed that the area between the tropics would experience extreme heat, leading to the creation of a designated hot belt on Earth. In this region, the Earth’s surface is consistently warmed by the rays of the sun, resulting in warm temperatures throughout the year and minimal fluctuations.
On the other hand, beyond the polar circles where the Sun rises low and can even be absent for up to six months, there exist cold belts. Due to the low position of the Sun in the sky, the Earth’s surface in these areas experiences only minimal heating, even during the summer months.
Between the polar circles and the tropics lie two temperate belts. In the northern and southern temperate belts, there is a noticeable shift in seasons, bringing about distinct changes in weather patterns.
The ball spins, however, the areas where its surface meets the axis of rotation stay still. These locations are referred to as poles.
On the Earth, there are specifically two points that do not partake in the rotation around the axis – these are the poles, namely the North Pole and the South Pole. What do we understand about them? The North Pole is essentially a frozen ocean bordered by continents. In contrast, the South Pole is a continent bordered by oceans.
Now consider this: how many straight lines can be drawn to connect the North and South Poles in a way that each point on the line is equidistant from them? It is evident that only one such line can be drawn, which represents the Earth’s axis of rotation. The Earth’s axis is tilted, with an inclination of 23.5 degrees with respect to the ecliptic plane. This tilt is accurately depicted on a globe, where a physical axis is used instead of an imaginary one.
On a globe, you can clearly see the outlines of continents, oceans, and seas, as well as their relative positions and sizes. However, the representations of geographical features on a regular school globe are quite small.
The largest rotating globe in the world, known as Erta, is situated in the town of Yarmouth, Maine, USA.

Erta has a diameter of 1,250 centimeters and weighs over 2,500 kilograms. The globe has been officially recognized in the Guinness Book of Records. This event occurred in 1999.
On this globe, the Earth’s surface is depicted in sufficient detail, but due to its size, it is very difficult to handle.
The Earth’s shape is nearly spherical and is technically referred to as the “geoid,” with an average radius of 6367 km.
The Earth rotates on its axis, completing a full revolution in 23 hours 56 minutes and 4 seconds. The Earth also revolves around the Sun, completing a full revolution in 365 days 6 hours 9 minutes 10 seconds, which is considered a year.

The radius of the Earth refers to the distance from its center to a specific point. However, there is an intriguing aspect to consider.
Let’s begin by establishing the definition and purpose of a radius. Essentially, a radius is a line segment that connects the center of a circle to any point on its circumference. In other words, it represents the length of this line segment. Additionally, it is equivalent to half of the circle’s diameter.
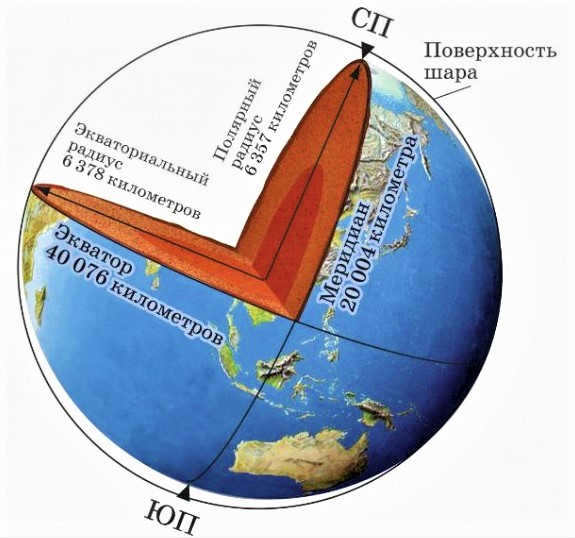
What is the possible radius of the Earth?
Currently, there are two main measurements:
- Equatorial radius: This represents the distance from the center of the Earth to the equator, measuring approximately 6378.1 km.
- Polar radius: This connects the center of the Earth to the geographic pole, which is estimated to be around 6356.8 km.
As we know, the Earth has both North and South poles. According to scientists, the polar radius is slightly shorter than the equatorial radius, measuring approximately 6356.8 km. This difference in length is attributed to the shape of the Earth.
As you are aware, our planet is not perfectly spherical, but rather slightly flattened at the poles. This results in a bulge at the equator, which causes an increase in the distance between two points. This phenomenon accounts for the variation in the distances in question.
Nevertheless, researchers have established the mean measurement of the Earth’s radius to be 6371 kilometers.
Consequently, when addressing the query regarding the Earth’s radius, one can rely on the average figure. Alternatively, it would be more accurate to specify that there exist two distinct measurements for this planetary characteristic.
It is also noteworthy to mention that the Earth’s radius is primarily computed in kilometers.
Evolution of Measurement throughout History
Without a doubt, ancient civilizations exhibited a keen interest in understanding their planet. Beyond simply observing the world around them, there was a dedicated pursuit of research and study focused on the Earth.

The ancient Egyptians made an observation that during the summer solstice, the rays of the sun reached the bottom of wells in Siena, an ancient city in Egypt. However, this phenomenon was not observed in Alexandria at the same time.
Eratosthenes of Cyrenaica used this observation to calculate the angle at which the Sun was positioned relative to the Earth. He determined that this angle was 7 degrees 12 minutes, which is equivalent to 1/50th of a circle.
Based on this finding, the scientist concluded that the distance between Siena and Alexandria was equal to this value. Since the geographical distance was 5 thousand stadia, the circumference of the Earth was calculated to be 250 thousand stadia.
1,500 years ago, it was commonly believed that the Earth occupied the central position in the universe. Five hundred years ago, it was widely accepted that the Earth had a flat shape, and just a few minutes ago, you were convinced that humans were the sole inhabitants of this planet. Ponder the possibilities of what you will come to “understand” tomorrow.
Men in Black.
The Earth’s Shape and Size
In ancient times, there were already theories suggesting that the Earth’s shape was not perfectly round.
Various scientists also attempted to measure the Earth’s radius. One example is Jean Richet, who observed Mars from Cayenne. He noticed that the period of motion of a seconds pendulum decreased compared to observations made in Paris. This observation provided evidence that the gravitational force is lower at the equator, indicating that the Earth’s shape is not a perfect circle.
Many others have also made efforts to understand the appearance of our planet, as the radius and diameter of the Earth are directly linked to its shape.
It should be pointed out that one of the most significant measurements of degrees was conducted by V. Y. Struve. The study was centered around measuring the arc spanning from the Danube to Finland, running along the western side of Russia.
Interestingly, the arc’s length exceeded 2800 kilometers and it spanned over 25 degrees, equivalent to approximately 1/14th of the total circumference of the planet.

Undoubtedly, over the course of history, individuals have expended significant efforts and made numerous endeavors to ascertain all the characteristics of our planet. At present, we possess a greater understanding than ever before. Furthermore, we have determined that the Earth possesses an average radius of 6371 kilometers. Moreover, modern scientific knowledge has enabled us to ascertain the diameter, the radius of the orbit, the distance from our planet to other celestial bodies, and a myriad of other details.
Gradually, albeit at a leisurely pace, we are unraveling the enigmas and challenges of the universe.
The Earth’s radius is a measurement of the distance between the Earth’s center and a point on its surface. The value of the Earth’s radius ranges from 6378 kilometers (3963 miles) at the equator to 6357 kilometers (3950 miles) at the pole. In astronomy and geophysics, the nominal radius of the Earth is sometimes used as a unit of measurement, denoted by the symbol R ⊕. In other contexts, it may be denoted as RE > or sometimes R e EN > _ . > ^ >> .
There are several alternative methods to determine and measure the Earth’s radius. Here are a few examples:
- 1 Introduction
- 1.1 The physics of Earth deformation
- 1.2 Radius and local conditions
- 2.1 Equatorial radius
- 2.2 Polar radius
- 3.1 Geocentric radius
- 3.1.1 Geophysical Extremes
- 3.2.1 Principal cross sections
- 3.2.1.1 Meridional
- 3.2.1.2 Primary vertical
- 3.2. 1.3 Partial values
- 4.1 Average radius
- 4.2 Autal radius
- 4.3 Volumetric radius
- 4.4 Radius of straightening
- 4.5 Mean curvature
- 4.6 Mean distance from center to surface
Introduction
Scale diagram depicting the compression of the 2003 IERS reference ellipsoid, with the top oriented towards the north. The circle is represented by the blue region. The outer edge of the dark blue line corresponds to an ellipse with the same minor axis as the circle and the same eccentricity as the Earth. The Karman line at an altitude of 100 kilometers (62 miles) above sea level is depicted by the red line, while the yellow area represents the altitude range for the International Space Station in low Earth orbit.
The shape of the Earth deviates from a perfect sphere due to factors such as its rotation, variations in internal density, and external tidal forces. This deviation is further increased by local topography, resulting in a complex and varied surface. When describing the Earth’s surface, we must simplify it to some extent. Therefore, we create models that approximate its characteristics, usually using the simplest model that meets our needs.
Each commonly used Earth surface model incorporates the concept of a geometric radius. Strictly speaking, only spheres have a radius, but the term radius is widely used in various fields, including those related to Earth models. Here is a partial list of Earth surface models, arranged from most accurate to less accurate:
- The actual surface of the Earth
- A geoid is a representation of mean sea level at each point on the actual surface
- A spheroid, also known as an ellipsoid of rotation, is used for modeling the entire Earth geocentrically or for regional work geodesically
- A sphere is another model used
When dealing with geoids and ellipsoids, the fixed distance from any point on the model to a specified center is referred to as the “Earth radius” or “Earth radius at that point”. It is also common to refer to any average radius of a spherical model as the “Earth radius”. However, when considering the actual surface of the Earth, the term “radius” is rarely used because it is usually not practical. Instead, it is more useful to have an elevation above or below sea level.
Irrespective of the design, every radius falls within a polar minimum of approximately 6,357 km and an equatorial maximum of around 6,378 km (equivalent to 3,950 to 3,963 miles). As a result, the Earth differs from a flawless sphere by merely one-third of a percent, bolstering the spherical model in nearly all circumstances and validating the usage of the term “Earth radius.” While precise measurements may differ, the principles discussed in this article are applicable to any expansive celestial body.
Deformation of the Earth: Physics Explained
The Earth’s rotation results in a unique shape – a flattened ellipsoid or spheroid. This shape is characterized by a bulge at the equator and flattening at the North and South poles. Specifically, the equatorial radius (a) is greater than the polar radius (b) by about aq. The compression constant (q) can be calculated using the formula:
q = (2 * ω^2 * a^3) / (3 * G * M), where ω is the angular frequency, G is the gravitational constant, and M is the mass of the planet.
For the Earth, the inverse of q is approximately 289, which is close to the measured inverse flattening of 1/f ≈ 298.257. It’s important to note that the equatorial convexity is not static and is subject to change over time. While the bulge has been decreasing, since 1998 there has been an increase, possibly due to the redistribution of ocean mass caused by currents.
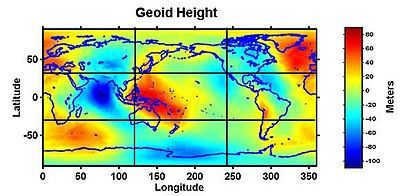
Variations in crustal density and thickness lead to fluctuations in gravity over the Earth’s surface and over time. As a result, the average sea level does not align with the ellipsoid. This disparity is known as the geoid height, which can be positive above or outside the ellipsoid, and negative below or inside it. The geoid height on Earth typically does not exceed 110 meters (360 feet). However, it can experience significant changes due to seismic events like the Sumatra-Andaman earthquake or the melting of ice masses, such as in Greenland.
It’s important to note that not all deformations occur within the Earth itself. The gravitational pull exerted by the Moon or the Sun can cause the Earth’s surface at a particular location to shift by several tenths of a meter over a period of approximately 12 hours (known as Earth tide).
Radius and local conditions
Al-Biruni’s (973-1048) method for determining the radius of the Earth simplified the measurement of the circumference in comparison to measurements taken at two distant locations.
Considering the impact of local and temporal factors on surface elevation, the values provided below are based on a “universal” model that has been globally refined to achieve a level of accuracy within 5 m (16 ft) of the reference elevation ellipsoid and within 100 m (330 ft) of mean sea level (assuming the elevation geoid is disregarded).
Furthermore, it is possible to approximate the radius by examining the Earth’s curvature at a specific point. Similar to a torus, the curvature will be most pronounced (narrowest) in one direction (north-south on Earth) and less pronounced (flattest) in the perpendicular direction (east-west). The specific radius of curvature will vary based on the location and the measurement direction from that particular point. As a result, the true horizon distance at the equator is slightly shorter in the north/south direction compared to the east-west direction.
Therefore, the presence of different geographical features in a specific area makes it impractical to establish a single precise radius. Instead, researchers must rely on an idealized model. Over the years, numerous models have been devised following Eratosthenes’ initial calculation. These models typically take into account the local topography to determine the most suitable reference ellipsoid for the specific study area. However, with the advancements in satellite remote sensing technology and the widespread use of the Global Positioning System (GPS), more comprehensive global models have been developed. Although these global models may not be as accurate for regional studies, they provide the best overall representation of the Earth’s shape.
Adjusted dimensions
The subsequent dimensions are derived from the standardized ellipsoid of the World Geodetic System 1984 (WGS-84). The standardized ellipsoid is a theoretical surface, and the measurements taken from the Earth in order to calculate it have an error of ± 2 m, both in the equatorial and polar measurements. There can be significant variations caused by orographic discrepancies at certain locations. When determining the position of an observed location, using more precise values for WGS-84 dimensions may not necessarily lead to a proportional increase in accuracy.
The equatorial dimension value has been determined with an accuracy of 0.1 m in WGS-84. The polar dimension value in this section has been rounded to the nearest 0.1 m, which is expected to be suitable for most applications. If a more precise value for its polar dimension is needed, please refer to the WGS-84 ellipsoid.
The utilization of the stated radius is employed in the equations within this piece.
Equatorial radius
The equatorial radius of Earth, denoted as a or the major semi-axis, represents the measurement from the Earth’s center to the equator. It amounts to 6,378,1370 km (3,963,1906 mi). The equatorial radius is frequently utilized for the purpose of contrasting Earth with other celestial bodies.
Polar radius
The polar radius of the Earth, also known as the minor semi-major axis, refers to the distance from the center of the Earth to the North and South Poles. It measures approximately 6,356.7523 km (3,949.9028 mi).
Radii based on location
Geocentric radius
The geocentric radius, denoted as R(φ), represents the distance from the center of the Earth to a specific point on the surface of a spheroid at a given geodetic latitude φ. It can be calculated using the following expression:
R(φ) = √((a^2 * cos^2 φ) + (b^2 * sin^2 φ)) / √((a * cos φ)^2 + (b * sin φ)^2)
Here, a and b represent the equatorial radius and polar radius of the Earth, respectively.
- The center of the Earth is 6,384.4 km (3,967.1 miles) away from Mt. Chimborazo, making it the maximum distance.
- The center of the Earth is about 6,352.8 km (3,947.4 miles) away from the Arctic Ocean floor, making it the minimum distance.
Radii of curvature
Main Sections
There are two main sections of radii of curvature: along the meridional and straight-vertical normal sections. The curvatures can be calculated using equation (125) which is:
(EG – F2)κ2 – (eG + gE – 2fF)κ + (eg – f2) = 0 = det (A – κB), ) \, \kappa ^ – (eG + gE-2fF) \, \kappa + (eg-f^2) = 0 = \det (A- \kappa \, B),>
where the first fundamental form for the surface is given by equation (112) which is:
ds2 = ∑ijaijdwidwj = Edφ2 + 2Fdφdλ + Gdλ2 = \sum _ a_ dw^2 = E \, d\varphi^2 + 2F \, d\varphi \, d\lambda + G \, d\lambda^2, >
E, F and G are components of the metric tensor :
r = [r 1, r 2, r 3] T = [x, y, z] T , r hat , g hat ] hat = [x, y, z] hat > , weight 1 = φ = \ varphi> , weight 2 sign equals λ, <\ displaystyle w hat = \ lambda,>
in the second fundamental form for the surface (Equation (123) in):
2 D = ∑ ijbijdwidwj = ed φ 2 + 2 fd φ d λ + gd λ 2, b_ dw hat dw hat = e \, d \ varphi hat + 2f \, d \ varphi \, d \ lambda + g \, d \ lambda hat ,>
e, f and g are components of the shape tensor:
normal to the surface in r .
With F = f = 0 for a flattened spheroid, the curvature is equal to
Geometrically, the second fundamental form gives the distance from r + dr to the tangent plane in r .
meridional
In particular, the curvature radius of the Earth in the north-south direction at φ:
M(φ) = R₁ = (ab)²((a cos φ)² + (b sin φ)²)^(3/2) = a(1 – e²)(1 – e² sin² φ)^(3/2) = 1 – e² a² N(φ)^(3) = > (a \ cos \ varphi)² + (b \ sin \ varphi)²)^(3/2) = <\ frac <(1-e² sin² \ varphi)^(3/2) >>> = <\ frac <1-e² > > N(\ varphi)³. >
Straight vertical
If a point is located directly east of another point, we can estimate the curvature in the east-west direction.
This curvature can be measured as the radius of curvature in a vertical perpendicular (also known as normal or orthogonal) to the meridian at a geodetic latitude φ:
This radius is also known as the transverse radius of curvature. At the equator, N = R. B. R. Bowring provides a geometric explanation, stating that this is the distance from the surface to the polar axis measured perpendicularly.

The Earth has three different radii depending on its latitude. R is the geocentric radius, M is the meridional radius of curvature, and N is the simple vertical radius of curvature.
Specific values
At the equator, the meridional radius of curvature of the Earth is equal to the meridian half-width of the rectum:
The polar radius of curvature of the Earth is equal to:
Directed
The curvature formula of Euler allows us to derive the radius of curvature of the Earth along a course with an azimuth (measured clockwise from north) α at a point φ.
Combinations
There is the possibility to combine the principal radii of curvature mentioned above in a way that is not directional.
The Gaussian curvature, K = κ1κ2 = det B det A, can be expressed as kappa_, and the Gaussian radius of curvature of the Earth at latitude φ is equal to this value.
Global mean radii
The Earth can be represented as a sphere in various ways. This section provides an overview of common methods. The radii presented here are based on the dimensions of the Earth derived from the WGS-84 ellipsoid:
a = Equatorial radius (6378.1370 km)
b = Polar radius (6356.7523 km)
The sphere is an approximate representation of a spheroid, which itself is an approximation of a geoid. The units used here are in kilometers, which are more suitable for geodesy compared to millimeters.
Average radius
Equatorial (a), polar (b), and mean radius of the Earth as defined in the 1984 edition of the World Geodetic System (not to scale)
In the field of geophysics, the International Union of Geodesy and Geophysics (IUGG) defines the mean radius (denoted R 1) as
For the Earth, the average radius is 6,371.0088 kilometers (3,958.7613 miles).
In the realm of astronomy, the International Astronomical Union designates the nominal equatorial radius of the Earth as R e EN > _ > > ^ >>, which is defined as 6,378.1 km (3,963.2 miles). The nominal polar radius of the Earth is defined as R p EN > _ > ^ >> = 6,356.8 km (3,949.9 miles). These values correspond to the radii of zero tide. The equatorial radius is typically used as the nominal value unless a polar radius is explicitly required.
Authalic Radius
The authalic radius, also known as the “equal area” radius, refers to the radius of an imaginary sphere that has the same surface area as a given reference ellipsoid. In the field of geodesy, this radius is denoted as R 2 by the International Union of Geodesy and Geophysics (IUGG).
A closed form solution is available for calculating the authalic radius of a spheroid:
where e = a – b / a, and A represents the surface area of the spheroid.
For our planet Earth, the authalic radius is approximately 6,371.0072 km (or 3,958.7603 miles).
Volumetric radius
Another way to describe a spherical model is by using the volumetric radius, which is the radius of a sphere with the same volume as the ellipsoid. The International Union of Geodesy and Geophysics (IUGG) refers to this as R3.
For the Earth, the volumetric radius is 6,371,0008 kilometers (3,958.7564 miles).
Straightening radius
Another type of mean radius is the straightening radius, which is the radius of a sphere with a circumference equal to the perimeter of any polar cross section of the ellipsoid. Calculating this radius requires an elliptic integral, using the polar and equatorial radii:
Mr = 2π ∫₀ˡπ/₂ (a²cos²φ + b²sin²φ) dφ.
The rectification radius is equivalent to the meridional mean, which is the average value of M:
When integrating from 0 to π/2, the integrals for the rectification radius and the mean radius yield the same outcome, which is 6,367.4491 km (3,956.5494 miles) for the Earth.
The semicubic mean of the two axes provides a good approximation for the meridional mean, differing from the exact result by less than 1 μm (4 × 10 in.). Alternatively, the average of the two axes, approximately 6367.445 km (3956.547 mi), can also be utilized.
Average Curvature
The average curvature at every point on the surface is determined by calculating the weighted average of the Gaussian curvature in all directions.
For the WGS 84 ellipsoid, the average curvature measures 6,370.994 km (3,958.752 mi).
Average Distance from Center to Surface
Most global mean radii are estimated based on an ellipsoid that closely approximates the geoid, although the geoid is not directly related to the surface topography. Another approach involves averaging the heights across the entire surface, resulting in an average radius that is 230 m larger than the average radius calculated by IUGG, autonomous radius, or volume radius. This average distance measures 6371.230 km (3958.899 mi) with a margin of error of 10 m (33 ft).
Sphere that moves back and forth
Official data
This chart presents the acknowledged figures for the circumference of the planet Earth.
| IAU | nominal “zero tide”, equatorial | 6378100 |
| IAU | nominal “zero tide” polar | 6356800 |
| IUGG | equatorial radius | 6378137 |
| IUGG | minor semi-axis (b) | 6356752.3141 |
| IUGG | polar radius of curvature (c) | 6399593.6259 |
| IUGG | mean radius (R 1) | 6371008.7714 |
| IUGG | sphere radius of the same surface (R 2) | 6371007.1810 |
| IUGG | radius of a sphere of the same volume (R 3) | 6371000.7900 |
| IERS | WGS-84 ellipsoid, major semi-major axis (a) | 6378137.0 |
| IERS | WGS-84 ellipsoid, minor semi-axis (b) | 6356752.3142 |
| IERS | WGS-84 first eccentricity square (e) | 0,00669437999014 |
| IERS | WGS-84 ellipsoid, polar radius of curvature (c) | 6399593,6258 |
| IERS | WGS-84 ellipsoid, mean radius of semi-major axes (R 1) | 6371008.7714 |
| IERS | WGS-84 ellipsoid, radius of sphere of equal dimensions a (R 2) | 6371007.1809 |
| IERS | WGS-84 ellipsoid, radius of sphere of equal volume (R 3) | 6371000.7900 |
| GRS 80 major semi-axis (a) | 6378137.0 | |
| GRS 80 minor semi-axis (b) | ≈6356752.314140 | |
| Spherical Earth Approx. radius (R E) | 6366707.0195 | |
| Meridional radius of curvature at the equator | 6335439 | |
| Maximum (Mt. Chimborazo) | 6384400 | |
| Minimum (half of the Arctic Ocean) | 6352800 | |
| Average distance from the center to the surface | 6371230 ± 10 |
Historical Background
The concept of Earth’s size was first documented in approximately 350 BC, when Aristotle mentioned in his book “On the Heavens” that mathematicians speculated that the Earth’s circumference was around 400,000 stadia. Scholars have interpreted Aristotle’s estimation as ranging from highly accurate to nearly double the actual value. The initial scientific measurement and calculation of Earth’s circumference were conducted by Eratosthenes around 240 BC. The accuracy of Eratosthenes’ calculations has been estimated to range from 0.5% to 17%. The uncertainty in both Aristotle and Eratosthenes’ estimations is attributed to the lack of clarity regarding the length of the stadium they referred to during their time.