astro.wikisort.org – Science
Upper Culmination (astronomy) – The moment when the center of a celestial object crosses the celestial meridian during its daily motion. In other words, it is the moment when the center of a celestial object reaches the highest point of intersection between its daily path and the celestial meridian.
Throughout the day, all celestial bodies cross the celestial meridian twice. The luminary is divided into an upper and lower culmination. When the luminary’s declination remains constant throughout the day, the luminary reaches its highest point during the upper culmination and its lowest point during the lower culmination. For celestial bodies that are not ascending, both culminations occur above the observer’s horizon. For both ascending and descending celestial bodies, the upper culmination takes place above the horizon, while the lower culmination occurs below the horizon. For celestial bodies that are not ascending, both culminations occur below the horizon and cannot be observed [1].
The upper culmination of a celestial body is distinguished by its position to the north or south of the zenith. When a celestial body culminates to the south of the zenith, its astronomical azimuth at the moment of culmination is 0°. Conversely, when a celestial body culminates to the north of the zenith, its azimuth at the moment of culmination is 180°.
By knowing the declination of the celestial body (δ) and the latitude of the observation site (φ), we can calculate the zenith distances of the celestial body at the moments of culmination, at the top:
z ↓ = ( φ + δ ) – 2 φ e P =(\varphi +\delta )-2\varphi _>
In the same way that positive values are assigned to northern geographic latitude and northern declination, while southern declination is considered negative, we can also assign a sign and zenith distance. It is convenient to follow this rule: if the shadow of the observer (real or imaginary) of the luminary falls on the northern side (which is positive), then the zenith distance of the luminary is positive. Conversely, if the shadow falls on the south, the zenith distance is negative. The same rule can be derived from considering the astronomical azimuth of the luminary: when the luminary reaches its highest point south of the zenith, the astronomical azimuth is 0°, and cos(0°) = +1. On the other hand, when it reaches its highest point north of the zenith, the azimuth is 180°, and cos(180°) = -1. In algebraic terms, the sign of the zenith distances can be determined through calculations that adhere to the conventions of the signs of latitude and declination.
By observing the upper and lower culminations of a prominent celestial body, one can determine its declination as well as the latitude of the place where the observation is taking place:
By observing the upper culminations of stars on opposite sides of the zenith at similar zenith distances, one can also calculate the latitude. To achieve this, it is necessary to know the declination of both stars, which significantly increases the accuracy of the measurement. This particular method is referred to as the Talcott method. If the North Star is in the upper culmination, the formula for calculation is as follows [2]:
If the North Star is in the lower culmination, the formula is as follows:
The symbols N and S represent the zenith distances and declinations for the North and South stars, respectively.
Related Articles
Important Information
- 10. LUMINOUS CULMINATION(unpublished). . stu.sernam.ru. Date of publication: October 3, 2016.Archived on October 11, 2016.
- Serapinas B. B.Basis of Geodetic Mapping(unpublished). . Faculty of Geography, Moscow State University. Date of publication: August 25, 2020.Archived on April 21, 2021.
Literature
- Kononovich E. V., Moroz V. I. – General course of astronomy, “Unitorial Urss”, 2001 (2nd ed. 2004)
- V. E. Zharov – Spherical Astronomy, “Vek-2”, 2006.
References
Stars of the north and south hemispheres. Upper and lower culminations of celestial bodies. Formula for calculating geographical latitude based on the altitude of a celestial body at culmination. Celestial meridian, ecliptic, and zodiac constellations. Celestial coordinates, star charts, and globes.
Students, graduate students, and young scientists who utilize the knowledge base for their studies and professional endeavors will greatly appreciate your assistance.
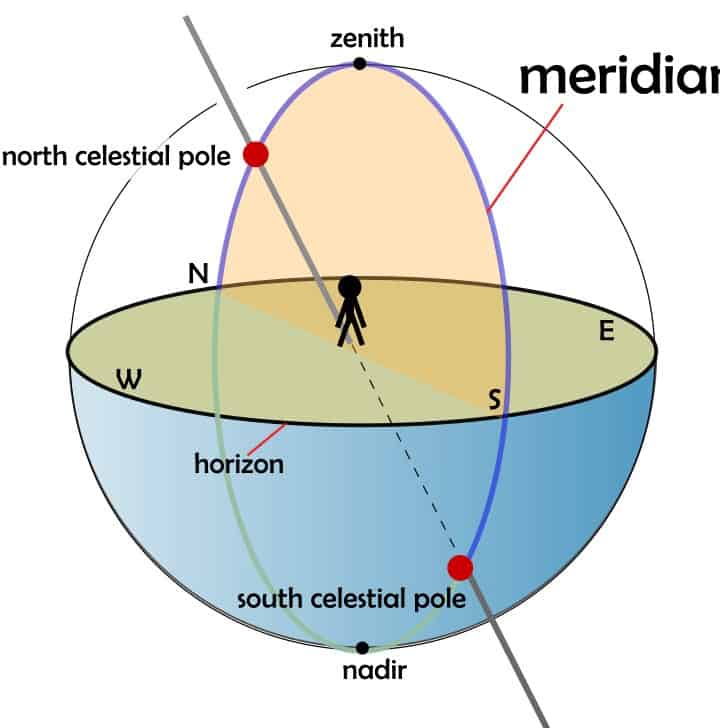
The daily rotation of the Earth and the movement of celestial bodies
The daily movement of celestial bodies
All celestial bodies traverse the sky, completing one full rotation every day. This phenomenon is a result of the Earth’s rotation. However, each celestial body moves in a distinct manner. For an observer situated at the North Pole, only the stars of the northern hemisphere are visible above the horizon. These stars revolve around Polaris and never dip below the horizon. Conversely, an observer at the South Pole can only observe the stars of the southern hemisphere. At the equator, both the stars of the northern and southern hemispheres can be observed in the sky.
At a given latitude of the place of observation, stars can both rise and set, as well as not rise and not set. For instance, in Russia, the stars of the Southern Cross constellation cannot be seen as it does not rise at our latitudes. On the other hand, the constellations of the Dragon and the Little Bear are non-setting constellations. The moment when a luminary passes through the meridian is known as the culmination. During the upper culmination, the luminary’s altitude, h, is at its maximum, while during the lower culmination, it is at its minimum. The time between the culminations of the luminaries is equal to 12 hours (half a day).
The culmination of luminaries at the upper and lower points
The height of the luminaries at their highest point, known as the upper culmination, is calculated as h = 90° – ts + e. Conversely, the height of the luminaries at their lowest point, known as the lower culmination, is calculated as h = ts + e – 90°. Each day, the sun and other luminaries rise in the eastern side of the sky and set in the west. At noon local time, the sun reaches its highest altitude, while at midnight it reaches its lowest culmination. In the polar regions, during the summer, the sun never sets below the horizon, allowing for observation of its lower culmination. In the middle latitudes, the visible daily path of the sun varies throughout the year, reaching its smallest size on the winter solstice (around December 22) and its largest size on the summer solstice (around June 22). On the days of the vernal and autumnal equinoxes (March 21 and September 23, respectively), the length of the day equals the length of the night, as the sun is positioned on the celestial equator, rising in the east and setting in the west.
The motion of the celestial bodies across the heavens
During their daily journey, the celestial bodies cross the celestial meridian twice – once in the south and once in the north. The moment at which a celestial body reaches its highest point above the horizon is called its culmination. When a celestial body is at its highest point in the south, it is at its greatest height above the horizon. It is known that the height of the celestial pole above the horizon (angle RON) is hp = f. Therefore, the angle between the horizon (NS) and the celestial equator (QQ1) is equal to 180° – f – 90° = 90° – f. The angle MOS, which represents the height of the celestial body M at its culmination, is the sum of two angles: Q1OS and MOQ1. We have just determined the value of the first angle, and the second angle is simply the declination of the celestial body M, which is equal to 8. Thus, we have the following formula that relates the height of a celestial body at its culmination to its declination and the geographic latitude of the observation location:
The movement of the Sun against the backdrop of the stars is an observable phenomenon that occurs as a result of the Earth’s annual revolution around the Sun. This creates the ecliptic, which is the path on the celestial sphere where it intersects with the Earth’s orbital plane. In a single day, the Earth covers approximately 1/365th of its orbit, causing the Sun to move about 1 degree in the sky every 24 hours. The duration of time it takes for the Sun to complete a full circle on the celestial sphere is known as a year. As you may recall from your geography lessons, the Earth’s axis of rotation is tilted at an angle of 66 degrees and 30 minutes with respect to its orbital plane. As a result, the Earth’s equator is inclined at an angle of 23 degrees and 30 minutes to the orbital plane. This inclination is what creates the angle between the ecliptic and the celestial equator, intersecting at two points known as the vernal and autumnal equinoxes.
During these specific days, which usually occur on March 21 and September 23, the Sun is positioned at the celestial equator and has a declination of 0°. This means that both the Northern and Southern Hemispheres of the Earth receive an equal amount of sunlight. The line separating day and night runs directly through the Earth’s poles, resulting in a day length that is equal to the night length across the entire planet. On the summer solstice, which takes place on June 22, the Earth’s Northern Hemisphere is tilted towards the Sun. This results in longer days and shorter nights in this part of the world, with the North Pole experiencing a continuous day. On the summer solstice, the Sun rises above the plane of the Earth’s (and celestial) equator at an angle of 23°30′. On the winter solstice, which occurs on December 22, the Sun is below the celestial equator at the same angle of 23°30′, leading to the Northern Hemisphere receiving the least amount of sunlight. The Sun’s height above the horizon at noon, known as its noon height, varies depending on its position on the ecliptic. By measuring the noon height of the Sun and knowing its declination on a given day, it is possible to calculate the geographical latitude of the observation location. This method has long been employed for determining one’s location on land and at sea.
Coordinates of celestial objects and astronomical charts
The naked eye can observe approximately 6000 stars across the entire celestial sphere, although only half of them are visible to us due to the Earth’s obstructive position. As the Earth rotates, our perspective of the sky shifts. Some stars are just beginning to rise from the eastern horizon, while others are directly overhead, and still others are setting behind the western horizon. This creates the illusion of the entire starry sky rotating as a cohesive unit. It is commonly understood that this rotation of the celestial sphere is actually an apparent phenomenon resulting from the Earth’s rotation. The motion of the starry sky caused by the Earth’s daily rotation can be captured using a camera.
If it were feasible to capture the trajectories of the celestial bodies in the heavens over the course of a full day, the resulting photograph would depict complete circles, totaling 360°. This is because a day signifies one complete rotation of the Earth on its axis. In the span of an hour, the Earth rotates a fraction equal to 1/24 of a circle, equivalent to 15°. Consequently, a star would trace an arc measuring 15° during this time, and half of that, or 7.5°, in half an hour. To indicate the positions of celestial bodies in the sky, a coordinate system similar to the one used in geography, known as the equatorial coordinate system, is employed. Just as geographic coordinates (latitude and longitude) are used to pinpoint any location on the Earth’s surface, the equatorial coordinate system utilizes a similar approach. In this system, the geographic longitude (f) is measured along the equator from the initial meridian (Greenwich), while the geographic latitude (L) is measured along the meridians from the equator to the Earth’s poles.
For instance, let’s take the city of Moscow. Its geographical coordinates are 37°30' East longitude and 55°45' North latitude. Now, let’s introduce a system of equatorial coordinates that indicates the relative position of celestial objects on the celestial sphere. To do this, we need to draw a line parallel to the Earth’s axis of rotation through the center of the celestial sphere, which we will call the world axis. This line will intersect the celestial sphere at two diametrically opposite points known as the poles of the world – P and P'. The North Pole of the world is the one where Polaris, also known as the North Star, is located. Furthermore, we can define a circle called the celestial equator by placing a plane through the center of the sphere parallel to the plane of the Earth’s equator. Just like the Earth’s equator, the celestial equator divides the celestial sphere into two hemispheres: the Northern Hemisphere and the Southern Hemisphere. The angular distance of a celestial object from the celestial equator is referred to as declination, which is represented by the Greek letter “delta”. Declination is measured along a circle that passes through the celestial object and the poles of the world, similar to how geographic latitude is measured on Earth.
Positive declination is assigned to luminaries located north of the celestial equator, while negative declination is assigned to those located south. The second coordinate, known as right ascension, is similar to longitude on Earth. It is represented by the Greek letter “alpha” and is measured along the celestial equator from the vernal equinox point, which is where the Sun is on March 21st each year. Right ascension is measured in the opposite direction of the apparent rotation of the celestial sphere. This means that luminaries rise and set in the order of their right ascension. In astronomy, right ascension is typically expressed in hours rather than degrees. As you may recall, due to Earth’s rotation, 15 degrees corresponds to 1 hour, and 1 degree corresponds to 4 minutes. Therefore, 12 hours of right ascension is equal to 180 degrees, and 7 hours and 40 minutes corresponds to 115 degrees. The process of creating a star map is relatively simple. First, we project all the stars onto a globe. Where the line connecting a star and the surface of the globe intersects, we mark the image of that star.
Typically, a star globe not only displays the stars, but also includes a grid of equatorial coordinates. A star globe is essentially a representation of the celestial sphere used for teaching astronomy in schools. While this model does not feature actual stars, it does depict the world axis, celestial equator, and other circles of the celestial sphere. However, star globes are not always the most convenient option, which is why maps and atlases have become popular in both astronomy and geography. By projecting all the points on the Earth’s globe onto a plane, such as the surface of a cylinder or cone, one can create a map of the Earth’s surface. Similarly, by performing this same operation with a star globe, a map of the starry sky can be obtained. Let’s now explore a basic movable star map. We can position the plane on which we wish to create the map so that it touches the globe’s surface at the location of the north pole of the world. Next, we project all the stars and the coordinate grid from the globe onto this plane. The resulting map will resemble geographical maps of the Arctic or Antarctic, with one of the Earth’s poles situated at the center.
The north pole of the world will be situated at the center of our star map, with Polaris next to it and the other stars of the Little Bear a little further away. The stars of the Big Dipper and other constellations that are near the world pole will also be included. The map will feature a grid of radially diverging rays and concentric circles to represent the equatorial coordinates. Numbers denoting direct ascent (from 0 to 23 h) will be written against each ray at the edge of the map. The ray that marks the beginning of direct ascent will pass through the vernal equinox, which is indicated by the Greek letter gamma. The declination will be counted on these rays from the circle representing the celestial equator, which is labeled 0°. Other circles on the map will also be marked, indicating the declination of the objects located on them. Stars will be represented on the map by circles of varying diameters, depending on their stellar magnitude. Stars that form characteristic constellation figures will be connected by solid lines, and the boundaries of constellations will be marked with dotted lines.
Other documents with similar content
Topics related to astronomy. Sources of information in the field of astronomy. The use of telescopes. Understanding constellations. Utilizing star charts. Navigating celestial coordinates. Using maps to locate celestial bodies. Calculating the culmination of celestial objects. Theorem regarding the height of the North Star. Measuring time in astronomy.
Exploring the subject and objectives of astronomy. Unique aspects of astronomical observations. The functionality of telescopes. Observing the daily movement of stars. Defining constellations and their various types. Understanding the ecliptic and the movements of planets. Utilizing star charts, celestial coordinates, and time measurements in astronomy.
The celestial sphere and its coordinate system are analyzed to determine the position of celestial luminaries in space. Geocentric coordinates are used to track the movement of these luminaries over time. The relationship between the observation point and the coordinates of the luminaries on the sphere is also studied.
Stars, as luminous celestial bodies, play a crucial role in navigation, orientation, and astronomical research. “Graduators” are used to measure stellar temperatures, and there are giants and dwarfs within the world of stars. The Earth’s movement through the constellations of the zodiac is also observed.
Evidence of the Earth’s axial rotation is important for understanding the geographical shell. Solar and stellar days have distinct characteristics, including the direction of motion and speed of orbital rotation. The changing illumination and heating of the northern and southern hemispheres throughout the seasons of the year are also studied.
The sequence of building the auxiliary celestial sphere and marking the stars on it. Spherical coordinate systems of the stars. The altitude line of position and its components. Local, standard, daylight saving, and nautical time, their relationship to Greenwich Mean Time. Navigational sextant.
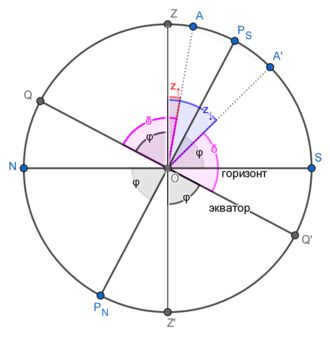
PS is an elevated pole (specifically the south pole), while line NS represents the observer’s horizon. ZZ’ represents the plumb line, and QQ’ represents the equator. Line AA’ is referred to as the diurnal parallel of the luminary. The angle φ represents the latitude of the observer’s location, δ represents the declination of the luminary, z↑ represents the zenith distance at the upper culmination, and z↓ represents the zenith distance at the lower culmination.
Culmination (astronomy) refers to the passage of the center of the luminary through the celestial meridian during its daily movement. Alternatively, it can be described as the passage of the luminary’s center through the point of intersection between the daily parallel of the luminary and the celestial meridian.
Throughout the course of the day, all celestial objects cross the celestial meridian twice. There is a clear distinction between the highest point and the lowest point that a celestial object reaches during its journey across the sky. If the declination of the celestial object remains constant throughout the day, its altitude will be at its peak during the highest point and at its lowest during the lowest point. For celestial objects that do not rise in altitude, both the highest and lowest points occur above the horizon. However, for celestial objects that rise and then descend, the highest point occurs above the horizon while the lowest point occurs below the horizon. In the case of celestial objects that do not rise in altitude, both the highest and lowest points occur below the horizon and are therefore not visible for observation [1].
By knowing the declination [math]\displaystyle< \delta >[/math] and the latitude [math]\displaystyle< \varphi >[/math] of the place where we are observing, we can determine the zenith distances of the luminary when it reaches its highest point:
The latitude of the elevated pole [math]\displaystyle< \varphi_>[/math] will be [math]\displaystyle< +90^\circ >[/math] for observers in the northern hemisphere and [math]\displaystyle< -90^\circ >[/math] for observers in the southern hemisphere.
In the same way that positive values are assigned to northern geographic latitude and northern declination, and negative values to southern declination, we can also assign a sign to the zenith distance. It is convenient to follow this rule: if the shadow of the observer (real or imaginary) of the luminary falls on the northern side, the zenith distance of the luminary is positive, and if it falls on the southern side, the zenith distance is negative. The same rule can be derived from considering the astronomical azimuth of the luminary: when the luminary is at culmination south of the zenith, its astronomical azimuth is 0°, and \cos(0°)=+1; when it is at culmination north of the zenith, the azimuth is 180°, \cos(180°)=-1. Mathematically, the sign of the zenith distances can be determined by taking into account the conventions for the signs of latitude and declination.
By making observations of a celestial body when it reaches its highest and lowest points in the sky, one can determine its declination and the latitude of the place where the observation is taking place:
By observing the highest points of stars on opposite sides of the point directly overhead at similar distances from the zenith, one can also determine latitude. To do this, it is necessary to know the declination of both stars, but this method greatly increases the accuracy of the measurement. This technique is known as the Talcott method. If the North Star is at its highest point, the formula is as follows [2]:
If the North Star is at its lowest point, the formula is as follows:
The symbols [math]\displaystyle< N >[/math] and [math]\displaystyle< S >[/math] represent the distances from the zenith and the declination for the North and South stars, respectively.
Related Content
Important Points
- ↑10. LUMINOUS CULMINATION(not published) . stu.sernam.ru. Accessed on October 3, 2016.Archived on October 11, 2016.
- ↑Serapinas B. B.Geodetic foundations of maps(not published). . Faculty of Geography, Moscow State University. Date of distribution: August 25, 2020.Archived on April 21, 2021.
Literature
- Kononovich E. V., Moroz V. I. – General course of astronomy, “Unitorial Urss”, 2001 (2nd ed. 2004)
- V. E. Zharov – Spherical Astronomy, “Vek-2”, 2006.
Hello, dear readers of the blog KtoNaNovenkogo.ru. When examining literary works, we often encounter the term “climax”, but we don’t always grasp its meaning.
Interestingly, this same concept also exists in music and astronomy. I wonder what connections there are between literary and musical art and the study of celestial bodies? Let’s attempt to unravel it.
What is a culmination.
Astronomy provides a visual representation of what a culmination is. It refers to the position of a celestial body when it passes the celestial meridian as it moves across the sky. This signifies the peak of activity, as if it is in the middle of the sky.
In music and literature, a culmination is the moment of highest tension in the development of a work. Musicologists and literary scholars argue that there can be multiple climaxes, both main and subsidiary. The main climax represents the peak of the plot, followed by a release of tension and resolution of conflict.
You and I have a strong interest in the genre of fiction. Whether it’s a short story, novella, novel, poem, or play, we enjoy the way events unfold and replace each other. These works often feature a diverse cast of characters with conflicting interests and actions, creating a rich tapestry of artistic conflict.
It’s important to note that conflict doesn’t always manifest as a physical struggle, such as a duel or hand-to-hand combat. In fact, conflict is often an internal tension, a clash of contradictory points of view.
The climax of a story is the pinnacle of this conflict, the point of maximum tension. It’s at this moment that we realize the previous course of events is no longer sustainable, and something new must happen. We’re on the edge of our seats, waiting for that next exciting development.
For instance, the novel Oblomov by I.A. Goncharov presents a clash between the ideology of “life creators,” individuals who are actively engaged in work, and the passive rejection of external activities.

Oblomov and Stoltz represent the two extremes in the novel, and Ilya Ilyich’s love for Olga serves as the pinnacle of the story, bridging the gap between these two poles.
In a way, the conflict can be likened to the build-up of tension in a thundercloud. As heavier particles collide with lighter ones, tension is created. The climax, then, can be seen as the moment when lightning strikes, followed by thunder (the plot’s denouement) and eventually the storm itself with rain and wind (the resolution of the conflict).
How to spot the climax in a written work
Identifying the climax in a text can sometimes prove challenging, especially when it occurs multiple times throughout the piece. However, there exist several indications that will undoubtedly help in making it unmistakable:
- All the characters’ interests converge on a particular event happening in a specific time and place;
- The main plot lines intertwine, converging at a single point;
- The tempo of events accelerates;
- The emotional tension reaches its peak;
- The climax is followed by the denouement, the resolution of the conflict that releases inner energy and subsequent tension.
A well-crafted story or novel provides the reader with an instinctive anticipation of the impending climax, causing the heart to beat faster.
Ironic literary pieces cleverly manipulate the anticipation of a catastrophic event: they skillfully draw out the sense of impending doom, only to shift focus to something trivial and inconsequential. A prime example of this technique is Vadim Levin’s renowned poem centered around Mr. and Mrs. Bockley, who engage in the peculiar activity of piercing nuts with binoculars.

Instances of climactic moments in literary pieces
Let’s explore different scenarios using the works of F.M. Dostoevsky as examples. In the novel “The Idiot“, there are several climaxes.
- The first one occurs during Nastasia Filippovna’s birthday celebration in the first part of the novel. This event not only introduces the main characters but also showcases the collision of various interests such as money, career, and love.
- Another pivotal moment takes place at Prince Myshkin’s birthday party in Pavlovsk, which is followed by mysterious occurrences.
- Lastly, the murder of Nastasia Filippovna by Rogozhin serves as the third pivotal moment, breaking away from the main storyline. Essentially, it acts as the resolution, a natural consequence of the conflict’s resolution. The actual event is not depicted directly, but its impact reverberates like a sudden thunderclap, foreshadowing the finale.
The climax intensifies the dramatic effect of the literary work. You can sense its approach – bury your head under the covers and await the denouement.
Best of luck to you! I’ll see you soon on the pages of the KtoNaNovenkogo.ru blog.
This article falls under the following categories: