The law of universal gravitation has a long history that dates back to the contributions of several brilliant individuals. One of these figures is Nicolaus Copernicus, who lived nearly two centuries before the law was fully developed. This postulate has been shrouded in numerous tales and myths, ranging from the apple that revolutionized the understanding of physics during that era, to the well-known rivalry between Newton and Robert Hooke, both of whom vied for the credit of discovering the law of universal gravitation.

The true details of the story may be uncertain, but there are certain events and facts that have been documented and serve as significant milestones in our understanding of gravity.
When discussing the principles of classical mechanics, the name of Sir Isaac Newton is always brought up. This scientist completely changed the way his contemporaries perceived the world around them and, most importantly, he mathematically proved his assumptions, which remained unchallenged for many years after his death.
One of the fundamental concepts in modern physics, which sparked numerous scientific debates during its time, is associated with Newton’s name – the law of universal gravitation. Newton discovered this law in 1688 and published it alongside his famous three laws of motion, which laid the groundwork for the development of the science of motion.

If the description of the law of gravitation was limited to the way objects fall to the ground, it would not possess its appealing nature. The story behind its discovery includes a significant detail: as early as 1666, Newton was contemplating the movement of celestial bodies, specifically the moon. Even at that time, while aware of the satellite’s orbit around the Earth, the scientist sought to comprehend the underlying causes of this phenomenon. It was during this period that he witnessed an apple detaching from a branch and descending to the ground in close proximity.
This led to the hypothesis that the Earth’s impact is what prevents objects from hanging unsupported in the air and causes the Moon to follow its observed path. However, this hypothesis could not be immediately proven. After conducting extensive calculations, Sir Newton formulated the law of universal gravitation. Unfortunately, due to the distance between the satellite and our planet at that time being unfairly large, the results had a significant error. This error was unacceptable to Sir Newton, who was known for his meticulous nature. It was only 22 years later, when new and more accurate data became available, that Sir Newton was able to present his law to the public.
Discovery of the Law of Universal Gravitation: A Historical Perspective
The concept of gravitation has been pondered since ancient times, particularly in Ancient Greece. However, many of the proposed theories were quite distant from reality. In his correspondence with Edmund Halley, Isaac Newton acknowledged the contributions of his predecessors, including Ismael Bouillot (Bulliald), a French astronomer, Christopher Rene, an English mathematician, and Robert Hooke, an English scientist with expertise in multiple fields.
“If I have seen further than others, it is because I have stood on the shoulders of giants,” Newton once wrote in a private letter to Hooke. When we specifically consider the discovery of the law of universal gravitation, it is impossible to deny the significance of these brilliant minds. Newton’s own conjectures were undoubtedly influenced by the profound insights of his predecessors.
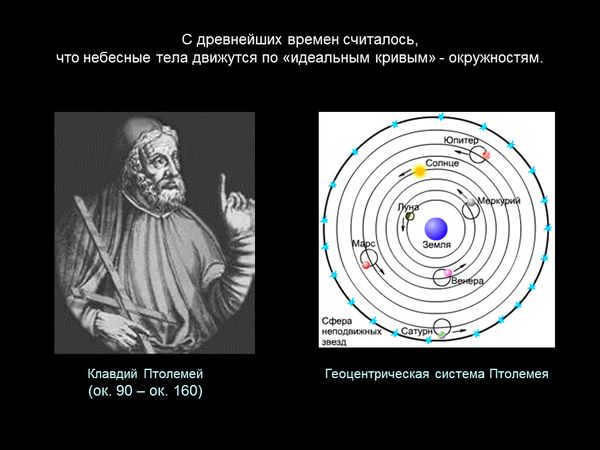
The origin of the exploration of the principle of universal gravitation commences with the Polish astronomer, Nicolaus Copernicus, and his composition “On the revolution of the heavenly spheres.” In this work, he introduced a groundbreaking theory for the 16th century, specifically the heliocentric model of the universe (wherein the planets orbit the sun).
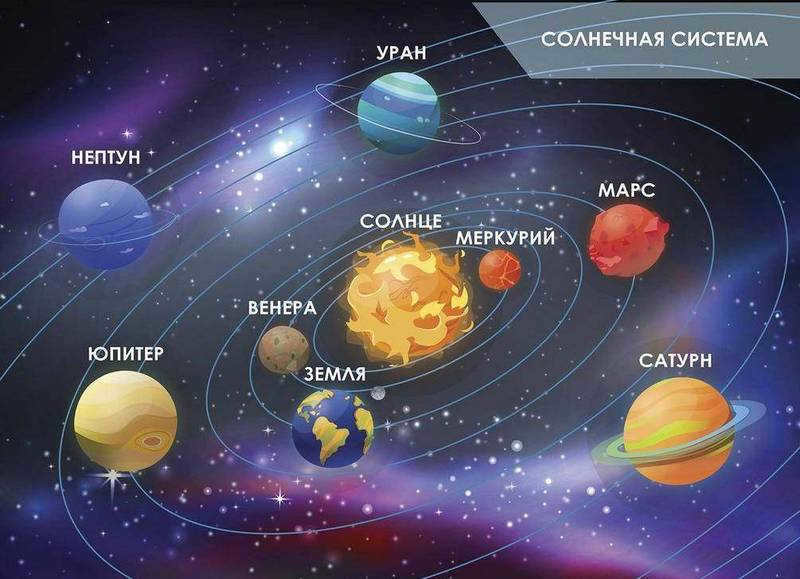
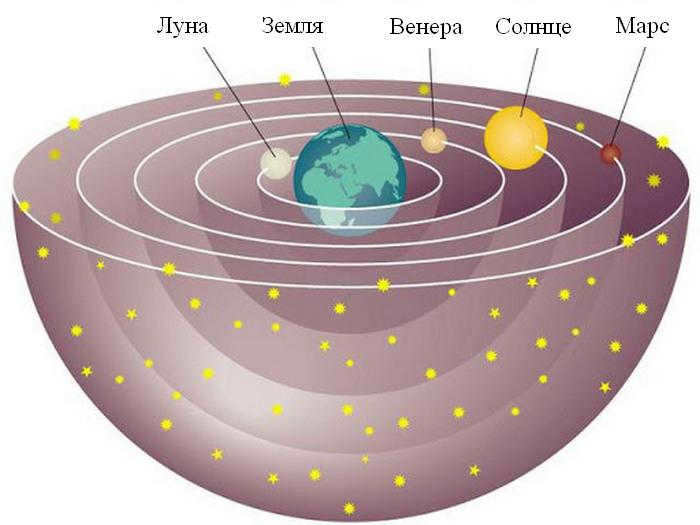
Prior to 1543, the widely accepted and unchallenged model of the universe was the geocentric model, which stated that all the planets and the sun revolve around the earth. This model was formulated by Ptolemy in the second century. However, after the publication of Copernicus’ book, significant alterations were demanded by the scientific community.
In his work, the astronomer did not specifically discuss gravitation, but Newton’s law has an impact not only on the Earth, but also on the entire Solar System. Therefore, in order to properly address the question of understanding the mechanism of the Universe (which is essentially the study of physics), it is crucial to recognize that our planet is not the center of the universe, a fact that was proven by Nicolaus Copernicus.
William Hilbert’s initial hypotheses
William Hilbert is widely recognized in the realm of electrical and magnetic phenomena research, but his contributions to mechanics should not be overlooked. Hilbert was an early proponent of Copernicus’ worldview, and what sets him apart as a precursor to Newton is his pioneering speculation on the nature of Earth and Moon’s gravitational forces.

The physicist’s posthumous work, which was published in 1603, suggests the scientist’s hypothesis that our planet and its satellite are massive magnets and, as a result, are drawn towards each other. Additionally, the work states that the Earth’s magnetic force is stronger due to the difference in their masses. While this overall speculation was somewhat reasonable, Hilbert inaccurately expressed the nature of the interaction: he mistakenly believed that the movement of the planets was caused by magnetism.
Discovering the Law of Universal Gravitation through Kepler’s Three Laws
Kepler’s laws, introduced between 1609 and 1618, played a crucial role in the development of the law of universal gravitation.
Tycho Brahe, an alchemist and astronomer from Denmark, served as Johannes Kepler’s mentor and made precise observations of planetary movements. Using these observations, Brahe created a comprehensive coordinate table. When Kepler inherited this valuable data, he noticed a consistent pattern in the planets’ motions. As a result, he formulated three laws that outlined the idealized heliocentric model of the solar system.
The first of Kepler’s laws states that all planets within the solar system revolve around the Sun in an elliptical path, with the Sun located at one of the focal points of the ellipse.
According to Kepler’s second law, the path of the planets as they orbit the Sun passes through the star. Additionally, if equal time intervals are measured and lines are drawn from the star to the planet, the areas they enclose will be of equal size.


Kepler’s third law can be expressed mathematically using the following ratio:
where T1,2 represents the periods of revolution of two planets around the Sun,
a1,2 denotes the lengths of the major semi-axes of the orbits of these planets.
One interesting aspect of Kepler’s laws is that he attributed the Sun with a significant role in the planetary motion, even before Newton. However, Kepler was unable to provide a theoretical justification for his conclusion. It was only later, when Newton discovered the underlying cause of these laws.
Together with Kepler’s contributions, Galileo’s investigations into the motion of falling objects also laid the foundation for Newton’s later breakthrough.
In the 16th century, Aristotle, the esteemed ancient Greek philosopher, firmly established the belief that an object would fall at a rate proportional to its mass. However, Galileo, in disagreement with this notion, conducted a series of experiments, one of which has become a well-known legend, although not documented in his own works. According to this tale, the Italian physicist dropped two balls of varying mass from the iconic Leaning Tower of Pisa and discovered that they landed nearly simultaneously. This experiment effectively refuted Aristotle’s theory, leading Galileo to formulate the laws of falling in his seminal work “Conversations and Mathematical Proofs of Two New Sciences” in 1638. According to these laws, the speed of falling increases with time, while the distance traveled increases in proportion to the square of time.
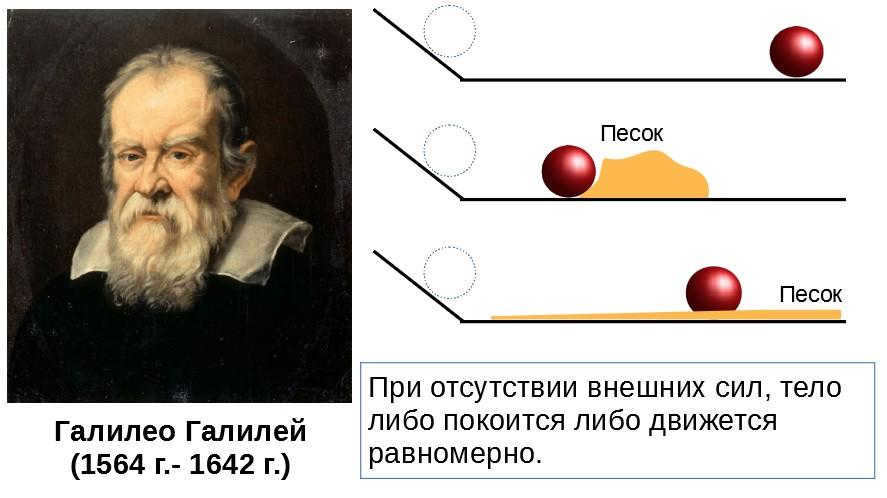

Furthermore, Galileo Galilei brought forth a fresh idea (presently known as inertia), demonstrating that an object will remain at rest or move in a straight line at a constant speed if no outside forces are exerted upon it. Newton would later reiterate this principle as the initial law of mechanics, half a century after Galileo first formulated it.
Proofs by Robert Hooke
Robert Hooke, a renowned scientist, made significant discoveries across various domains of physics, chemistry, and biology. However, his impulsive nature and constant disputes over authorship with fellow scientists often led to him being remembered as an envious and quarrelsome individual. The law of universal gravitation became a point of contention for Hooke, who asserted that he had formulated the principle long before Newton’s discovery. To some extent, this claim holds true.

In 1674, Robert Hooke published a treatise titled “An Attempt to Prove the Motion of the Earth,” in which he presented a brief and vague explanation of the concept of a universal force of gravity. However, it was in a letter dated January 6, 1680, that Hooke provided Isaac Newton with a more familiar formulation of the law and included mathematical calculations applicable to objects moving in circular orbits. Recognizing Newton’s expertise in mathematics, Hooke requested his assistance in further developing the law for elliptical orbits. Thus, it was this correspondence that marked the beginning of the documented history of the discovery of the law of universal gravitation.
Edmund Halley and his deductions from Kepler’s law
In 1684, the English astronomer Edmund Halley mathematically demonstrated the inverse relationship between gravity and the square of the distance, deducing this connection from Kepler’s third law.


Consequently, all the necessary conditions were in place to precisely articulate Newton’s gravitational theory and fully validate it mathematically.
Newton’s Solution to the Problem of Gravitation
In order to arrive at the ultimate formulation of the law of universal gravitation, Isaac Newton examined the movement of the Moon in relation to the Earth, taking into account the distances between the two celestial bodies. In developing the mathematical model, Newton heavily relied on his second and third laws of motion, which he had already established prior to this investigation.
Here’s an intriguing piece of information: the law of attraction, as we know it today, did not originally include the gravitational constant G. In fact, it wasn’t until the 19th century that physicists began incorporating this crucial factor into their works.
Discovering the Gravitational Constant’s Worth
In 1798, Henry Cavendish conducted an experiment to estimate the average density of the Earth using torsion weights developed by Charles Coulomb. The apparatus consisted of a torsion weight with two small balls at each end, with a larger ball introduced during the experiment. The gravitational interaction between the bodies caused the torsion weight’s head to deflect at a certain angle, which was measured using optical instruments. By analyzing this angle and the elasticity of the thread holding the arm, Cavendish was able to determine the force of attraction between the balls and subsequently calculate the previously unknown coefficient of proportionality.


After conducting his experiment, Henry Cavendish made a calculation which showed that the gravitational constant is equivalent to G = 6.754∙10 -11 m 3 / (kg∙s 2 ). Nowadays, this value is determined with even greater precision: G = 6.67384∙10 -11 N∙m²-kg -2 .
The determination of the coefficient of proportionality was just one of the many practical applications of the law of gravitation.
A Short Biography of the Renowned English Scientist, Isaac Newton
Born on the 4th of January, 1643, Isaac Newton’s early years were marked by adversity. His father, after whom he was named, passed away before his birth, leading his mother to remarry and leave Newton in the care of his relatives. Despite his fragile health, Newton displayed a keen interest in reading and had a knack for creating simple toys from a young age. However, his academic performance suffered during his early years in school, until a fortuitous event transformed his approach to learning. As a frail child, Newton was frequently targeted by his peers, leading him to recognize that he could not overpower them physically. Determined to rise above his tormentors, he resolved to outwit them instead.

In 1668, Isaac Newton earned a master’s degree upon returning to college and became a teacher at his alma mater. Later in life, the physicist developed a deep interest in alchemy, mathematical analysis, and conducted experiments in optics. He even invented an improved version of the telescope-reflector, which aided in the discovery of numerous astronomical objects.
Newton was known to be a solitary and introverted individual who preferred to keep his scientific findings to himself, due to the constant disputes and debates they would spark. Unfortunately, in the winter of 1677, a fire broke out in his home, destroying the majority of his manuscripts. To compound his losses, his friend Isaac Barrow passed away in May of the same year, a devastating blow for the scientist who had only managed to form close relationships with a select few.
In 1689, two years after the publication of the renowned “Principia”, its author embarked on a new venture in administration, representing his university in Parliament. However, in 1696, Newton made a permanent departure from the college and assumed the position of Mint Keeper.
Fascinatingly, during his time at the court, the physicist devised a minting technique that greatly reduced counterfeiting. This innovation involved adding small lines to the edges of the coins, a practice that is still employed today.
In 1703, Newton was elected president of the Royal Society, and in 1705, Queen Anne of Great Britain knighted him, making him the first recipient of such an honor for scientific achievements.
Sir Isaac Newton passed away on March 31, 1727, and it was reported that his funeral was attended by the entire city of London.
The discovery of the law of universal gravitation may appear simple at first glance, but in reality, it is the result of years of work by numerous scientists who gradually uncovered its secrets.
We now have the answer to the question What does Kepler’s second law imply? This should be sufficient for you to find the answer you are seeking.
Kepler’s Second Law, also known as the law of areas, states that each planet orbits in a plane that passes through the center of the Sun. In equal periods of time, the line connecting the Sun and the planet sweeps out equal areas. (Jun 18, 2021)
What is the main implication of Kepler’s second law?
Kepler’s second law implies that a planet’s movement around the Sun is not uniform, with a higher linear velocity at perihelion compared to aphelion.
What improvement did Newton make to Kepler’s third law?
Newton’s refinement to Kepler’s third law states that the force F’ acting on a planet from the Sun is equal to it modulo, (1) the force acting on any planet is directly opposite in direction and is equal to : where M is the mass of the Sun. Since F = F’, = . Let us denote where G is a constant quantity.
What is the explanation for Kepler’s first law?
Kepler’s first law states that each planet follows an elliptical orbit, with the Sun located at one of the foci.
What was the foundation of Kepler’s law discovery?
Kepler arrived at his laws by reasoning that if Earth has one moon and Jupiter has four, the number of moons increases exponentially.
What are the implications of Kepler’s second law? User Responses
For orbits that are circular in shape, the initial and second laws of Kepler are naturally fulfilled, and the third law asserts that T2 ~ R3, where T represents the orbit’s period and R denotes the radius of the orbit.
Therefore, it can be deduced from Kepler’s second law that the planet’s movement around the Sun is not uniform, with greater linear velocity at perihelion compared to aphelion.
Kepler’s second law is essentially the same as the law of conservation of momentum. Figure 1.24.3 illustrates the momentum vector of a celestial body, its components, and the corresponding area.
The first law of Kepler precisely states that the orbits of planets are ellipses, with one focus. This is precisely what is mentioned in the second law.
The second law of Kepler, also known as the law of areas
Hence, based on Kepler’s second law which states that the planet orbits the Sun in an unequal manner, it has a greater linear velocity at perihelion.
Therefore, according to Kepler’s second law, the planet moves around the Sun in a non-uniform manner, with a higher linear velocity at perihelion compared to aphelion.
Video answers explaining the implications of Kepler’s second law
Kepler’s Laws
Join the Astronomy Group – Home Science on VKontakte (https://vk.com/astromainscience) to learn more about the fascinating world of astronomy. Feel free to support us financially as well!

Lesson 65. The Laws of Planetary Motion According to Kepler

Law of areas
Kepler’s Laws
Laws Kepler’s laws! or the laws of planetary motion. All celestial bodies move in curved paths in accordance with the principles established by Johannes Kepler.
Johannes Kepler dedicated his entire lifetime to demonstrating that our solar system is a form of divine art. Initially, he attempted to establish that the arrangement of celestial bodies resembles the regular polyhedra found in ancient Greek geometry.
During Kepler’s era, there was knowledge of the existence of six planets. It was commonly believed that these planets were positioned within crystal spheres. Kepler, the scientist, hypothesized that these spheres were arranged in a manner that allowed for polyhedrons of precise shape to fit perfectly between neighboring spheres.
For example, there is a cube inscribed within the outer environment in which the sphere containing Jupiter and Saturn is inscribed. Similarly, there is a tetrahedron between Mars and Jupiter, and so on.
Laws
After years of studying the planets, Kepler’s observations led to the discovery of three laws. Let’s explore them in this article.
The first
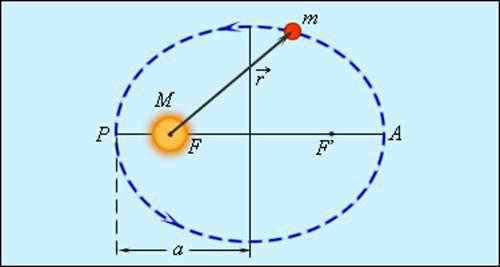
Kepler’s first law states that all the planets in our solar system follow a closed curve known as an ellipse. Our star, the Sun, is located at one of the foci of the ellipse. There are only two foci, which are two points inside the curve, and the sum of the distances from these foci to any point on the ellipse remains constant.
Through extensive observations, Kepler noticed that the orbits of all the planets in our solar system are nearly coplanar. Most celestial bodies follow elliptical orbits that are close to being circular. However, Pluto and Mars have more elongated orbits.
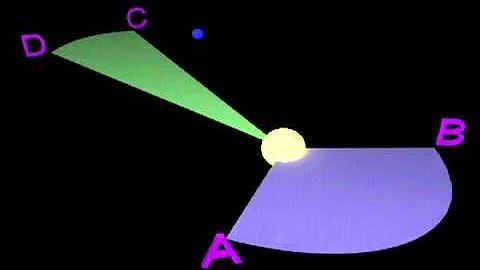
Kepler’s Second Law states that each planet moves in a plane that passes through the center of our star. Simultaneously, the radius-vector connecting the Sun and the planet describes equal areas.
Consequently, it is evident that the celestial bodies orbit the yellow dwarf in an uneven manner, with the maximum velocity at perihelion and the minimum at aphelion. This phenomenon is observable in the Earth’s motion. Every year, in early January, our planet accelerates as it reaches perihelion.
As a result, the Sun’s movement along the ecliptic is faster during this period compared to other times of the year. In early July, the Earth passes through aphelion, causing the Sun to move more slowly along the ecliptic.
The Law of Planetary Rotation
Kepler’s third law establishes a relationship between the period of rotation of planets around a star and their average distance from it. This law was applied by the scientist to all the planets in our solar system.
Understanding Kepler’s Laws
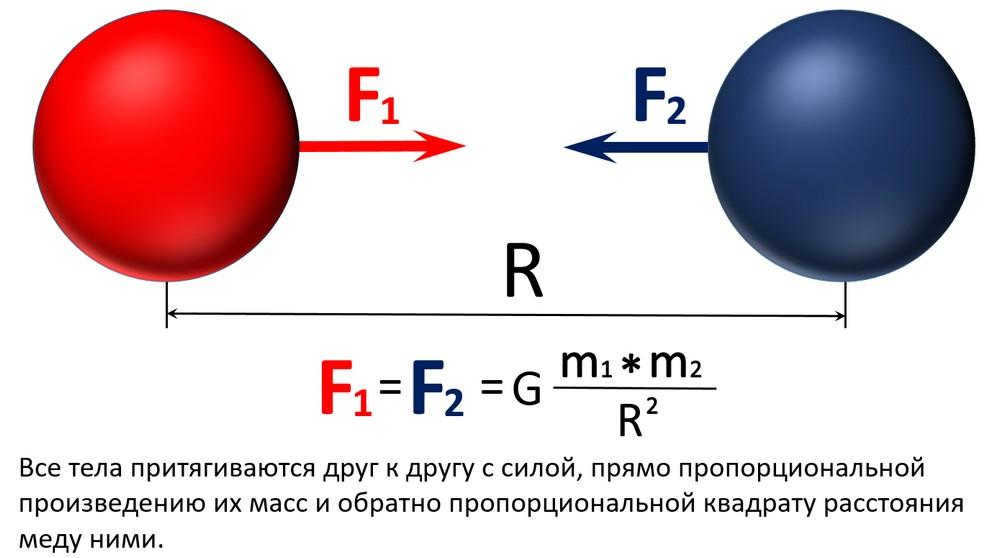
Kepler’s laws were able to be understood and explained after Newton discovered the law of gravitation. According to Newton, physical objects interact through gravitational forces. This force applies universally to all objects made of matter and physical fields. Newton stated that two stationary bodies exert a force on each other that is proportional to the product of their masses and inversely proportional to the square of the distance between them.
Actually, in our system, all objects are influenced by not only our star, but also by one another. As a result, no object can follow a perfectly elliptical, hyperbolic, or circular path. When an object deviates from Kepler’s laws during its motion, it is referred to as a perturbation, and the motion itself is known as perturbed motion. This is the type of motion that is considered to be genuine.
The elliptical orbits of celestial bodies are not fixed. The attraction from other bodies causes changes in the shape of the orbit.
The Contribution of E. Newton
Isaac Newton derived the law of universal gravitation from Kepler’s laws of planetary motion. This law of universal gravitation was then used by Newton to solve problems in space mechanics.
Following Isaac, advancements in celestial mechanics involved the development of mathematical science for solving equations based on Newton’s laws. Newton established that a planet’s gravity is determined by its distance and mass, while factors such as temperature and composition have no impact.

Newton’s scientific research revealed a discrepancy in the accuracy of the third Keplerian law. He emphasized the significance of factoring in a planet’s mass when conducting calculations, as the motion and weight of planets are interconnected. This harmonious combination establishes the correlation between the Keplerian laws and the law of gravitation discovered by Newton.
Astrodynamics
Astrodynamics emerged as a result of applying Newton’s and Kepler’s laws. It is a branch of celestial mechanics that focuses on studying the movement of artificially created celestial bodies, such as satellites, interplanetary stations, and various spacecraft.
Astrodynamics involves the calculation of spacecraft orbits and determining the parameters for launch, orbit selection, and necessary maneuvers. It also includes planning gravitational influences on spacecraft. These practical tasks are just a few examples of what astrodynamics deals with. The results obtained in this field are used in a wide range of space missions.
A closely related field to astrodynamics is celestial mechanics, which examines the movement of celestial objects in response to gravitational forces.
Orbits
An orbit is defined as the path followed by an object in a given space. In celestial mechanics, it is assumed that the object is significantly less massive than the body it is orbiting. In a rectangular coordinate system, the path can take the form of a conic section, such as a parabola, ellipse, circle, or hyperbola.
In other words, the path can be represented by a parabola, ellipse, circle, or hyperbola, with the focus coinciding with the center of the system.
This enabled him to uncover three laws that could explain the orbital movement of celestial objects. Kepler uncovered the subsequent components of an orbit: the form of the orbit, its inclination, the position of a body’s orbital plane in space, the size of the orbit, and the time reference. All of these components determine an orbit irrespective of its shape.
In computations, the primary coordinate plane may be the plane of the ecliptic, galaxy, planetary equator, etc.

Various research indicates that the shape of orbits can be either elliptical or circular in nature. They can be classified as either closed or unclosed. Orbits can also be categorized based on their inclination angle with respect to the Earth’s equatorial plane, such as polar, inclined, and equatorial orbits.
Orbits can also be classified based on their revolution period around a celestial body, such as synchronous or sun-synchronous orbits, synchronous-daily orbits, and quasi-synchronous orbits. As stated by Kepler, all celestial bodies have a specific velocity of motion, known as orbital velocity. This velocity can remain constant throughout the orbit or vary.
Johannes Kepler possessed a keen appreciation for beauty. Throughout his lifetime, he dedicated himself to demonstrating that the solar system was a form of mystical artwork. Initially, he sought to establish a connection between its structure and the five regular polyhedra found in classical ancient Greek geometry. (A regular polyhedron is a three-dimensional shape in which all faces are identical regular polygons.) During Kepler’s era, there existed six known planets that were believed to reside on rotating “crystal spheres”. Kepler contended that these spheres were arranged in such a manner that regular polyhedra fit precisely between adjacent spheres. For instance, between the outermost spheres of Saturn and Jupiter, he positioned a cube that was inscribed within the outer sphere, which in turn inscribed the inner sphere. Between the spheres of Jupiter and Mars, he placed a tetrahedron (a regular tetrahedron), and so forth. With six planetary spheres and five inscribed polyhedra in between, one might assume it to be the epitome of perfection?
Unfortunately, when comparing his model to the observed orbits of the planets, Kepler had to acknowledge that the actual behavior of celestial bodies does not conform to the slender framework he had outlined. As the modern British biologist J. A. Kepler aptly remarked, Kepler was forced to admit that the real behavior of celestial bodies did not fit into his outlined framework. Haldane (J.
B. S. Haldane, “the concept of the universe as a geometrically flawless masterpiece turned out to be another elegant hypothesis demolished by unappealing facts.
Kepler’s youthful impulse resulted in the creation of a unique model of the solar system, which he personally crafted and gifted to his patron, Duke Frederick von Wurtemburg. This exquisite metal artifact featured hollow containers in the shape of the planets’ orbital spheres and inscribed regular polyhedrons. These containers were intended to be filled with a variety of beverages, to be enjoyed by the Duke’s guests during celebratory occasions.
The historical importance of Kepler’s first law cannot be overstated. Prior to Kepler, astronomers held the belief that planets only moved in circular orbits. If observations did not align with this belief, they would add smaller circles that the planets traced around the main circular orbit. This was primarily a philosophical stance, considered an unquestionable fact that could not be doubted or verified.
It was believed by philosophers that the celestial structure, in contrast to the terrestrial structure, is flawless in its harmony. They argued that since the circle and the sphere are the most perfect geometrical figures, it follows that the planets must move in circular paths. I still find myself having to dispel this misconception among my students time and time again. However, Johannes Kepler was able to challenge this philosophical bias by examining Tycho Brahe’s extensive observational data. Through this examination, Kepler realized that the idea of circular planetary motion did not align with the facts. This realization was similar to Copernicus’ decision to remove the Earth from the center of the universe, despite the prevalent belief in a geocentric model. Both discoveries were made in the face of evidence that contradicted the established ideas about the behavior of planets in their orbits.

The initial two laws address the specificity of single planet’s orbital trajectories. Kepler’s Third Law enables the comparison of planets’ orbits to one another. It states that the further a planet is from the Sun, the longer it takes for it to complete a full revolution while orbiting, resulting in a longer “year” on that planet. Presently, we understand that this phenomenon is influenced by two factors. Firstly, the farther a planet is from the Sun, the greater the perimeter of its orbit. Secondly, as the distance from the Sun increases, the linear velocity of the planet decreases.
Kepler’s laws were formulated based on careful observations and analysis. He did not provide explanations for the causes of certain phenomena, such as the ellipticity of orbits or the equality of areas. These conclusions were simply derived from his study.
If you were to inquire about the orbital motion of planets in other star systems, Kepler would not have had any information to offer. He would need to gather new observational data, analyze it, and search for patterns. In other words, he would have no grounds to assume that the laws governing the Solar System apply universally to other planetary systems.
Kepler’s Third Law has been and continues to be a significant factor in contemporary cosmology. When astrophysicists observe distant galaxies, they detect faint signals emitted by hydrogen atoms orbiting at distances much greater than those of stars typically found in the galactic center. By analyzing the Doppler effect in the spectrum of this radiation, scientists are able to determine the rotational velocities of the hydrogen periphery of the galactic disk. From these velocities, they can also deduce the angular velocities of galaxies as a whole (see also Dark Matter). It is gratifying to see that the contributions of this scientist, who paved the way for our accurate understanding of the structure of our solar system, continue to play such a crucial role in the study of the vast Universe even today, centuries after his passing.
Between the planets Mars and Earth, there is a dodecahedron (a shape with twelve sides); between Earth and Venus, there is an icosahedron (a shape with twenty sides); and between Venus and Mercury, there is an octahedron (a shape with eight sides). Kepler presented this structure in a detailed volumetric drawing (see Kepler’s diagram) in his first book, The Cosmographic Mystery (Mysteria Cosmographica, 1596). – Translator’s note.
Historically, Kepler’s laws (like the beginnings of thermodynamics) are not numbered based on the order of their discovery, but rather according to the order in which they were understood by the scientific community. In reality, the first law was discovered in 1605 (published in 1609), the second in 1602 (published in 1609), and the third in 1618 (published in 1619). – Translator’s note.
Kepler’s laws are a set of physical laws discovered by Johannes Kepler that explain the movement of planets around the Sun.
Kepler’s First Law of Ellipses.
In Kepler’s First Law, each planet in the solar system follows an elliptical orbit with the Sun located at one of its foci.
The shape of the ellipse and how closely it resembles a circle can be determined by the ratio, where c is the distance from the center of the ellipse to its focus (half of the interfocal distance), a is the major semi-major axis. The value e represents the eccentricity of the ellipse. When c = 0 and e = 0, the ellipse becomes a circle.
Kepler’s Second Law (Law of Areas)
Kepler’s Second Law states that each planet orbits in a plane that passes through the center of the Sun. Furthermore, the radius-vector connecting the Sun and the planet sweeps out equal areas in equal times.
In our solar system, there are two terms associated with this law: perihelion, which refers to the point in the planet’s orbit that is closest to the Sun, and aphelion, which is the point furthest from the Sun. As a result of Kepler’s second law, the planet’s movement around the Sun is not uniform, with a greater linear velocity at perihelion compared to aphelion.
Each year in the beginning of January, the Earth accelerates as it passes through perihelion. As a result, the Sun appears to move faster along the ecliptic to the east compared to its average speed throughout the year. Similarly, in early July, when the Earth reaches aphelion, it decelerates causing the Sun’s movement along the ecliptic to slow down. According to the law of areas, the force that controls the orbital motion of the planets is directed towards the Sun.
Harmonic Law or Kepler’s Third Law
The relationship between the periods of orbital motion of planets around the Sun and the major semi-axes of their orbits can be expressed by the following equation: the squares of the periods (T1 and T2) are proportional to the cubes of the major semi-axes (a1 and a2).
Newton discovered that the gravitational attraction between a planet and the Sun is determined solely by the distance between them, regardless of other factors like composition or temperature. He also demonstrated that Kepler’s third law is not entirely accurate, as it takes into account the mass of the planet: , where M represents the mass of the Sun, and m and m denote the masses of the planets.
Given the connection between motion and mass, scientists utilize a combination of Kepler’s harmonic law and Newton’s law of gravitation to calculate the masses of planets and satellites. This method is applicable when the orbits and orbital periods of these celestial bodies are known.
Wikimedia Foundation. 2010.
Kepler’s Laws are a set of physical laws discovered by Johannes Kepler that describe the movement of planets around the Sun.
Kepler’s First Law (Law of Ellipses).
Kepler’s First Law states that each planet in the solar system orbits on an ellipse with the Sun at one of its foci.
The shape of the ellipse and its resemblance to a circle is determined by the ratio , where c is the distance from the center of the ellipse to its focus (half of the interfocal distance), a is the major semi-axis. The value e is known as the eccentricity of the ellipse. When c = 0 and e = 0, the ellipse becomes a circle.
Kepler’s Second Law (Law of Areas)
Kepler’s Second Law states that each planet orbits in a plane that passes through the center of the Sun. Additionally, the radius-vector connecting the Sun and the planet sweeps out equal areas in equal times.
In our solar system, there are two important terms related to this law: perihelion, which refers to the point in the planet’s orbit that is closest to the Sun, and aphelion, which is the point in the orbit that is farthest from the Sun. As a result of Kepler’s second law, the planet’s velocity varies throughout its orbit, with a higher linear velocity at perihelion compared to aphelion.
Each year, in the beginning of January, the Earth speeds up as it passes through perihelion. This causes the Sun to appear to move faster along the ecliptic to the east compared to its average movement throughout the year. Conversely, in early July, the Earth slows down as it passes through aphelion, causing the Sun’s movement along the ecliptic to decrease in speed. The law of areas states that the force controlling the orbital motion of the planets is directed towards the Sun.
Harmonic Law
The relationship between the periods of orbital revolution and the major semi-axes of the planets’ orbits around the Sun can be described using Kepler’s Third Law. It states that the squares of the periods, T1 and T2, are related to the cubes of the major semi-axes, a1 and a2.
Newton expanded upon Kepler’s Third Law by introducing the concept of gravitational attraction. He discovered that the gravitational attraction of a planet depends solely on its distance from the Sun, disregarding factors such as composition or temperature. Newton’s findings also revealed that Kepler’s Third Law is not entirely accurate, as it fails to account for the mass of the planet. The revised formula for the relationship between the periods, masses, and major semi-axes is: , where M represents the mass of the Sun, and m and m represent the masses of the planets.
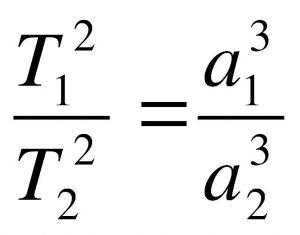
The combination of Kepler’s harmonic law and Newton’s law of gravitation is utilized to determine the masses of planets and satellites if their orbits and orbital periods are known, demonstrating the relationship between motion and mass.
Wikimedia Foundation. 2010.
It is difficult to fathom that in the past, people believed the Earth was flat. Ancient Greeks, for instance, envisioned the Earth as a plane floating in the air, surrounded by glaciers. In India, it was believed that the planet sat on three elephants standing on a tortoise. Although some individuals still hold these beliefs, there is substantial evidence proving that our planet is not flat. Here are a few examples to keep the conversation going.
Gravitational Forces
The force of gravity perpetually attracts all objects towards the central point of mass. The Earth, being spherical in shape, has its center of mass located at its center.
Gravity consistently pulls every object on the Earth’s surface in the direction of the planet’s core, which is downward, irrespective of their specific position. This phenomenon is consistently observed.
If we were to envision the Earth as a flat surface, gravity would need to pull all objects on the surface towards the center of the plane. Consequently, if one were to find themselves at the periphery of a flat Earth, gravity would pull them not downward, but towards the center of the disc.
In order to substantiate their claims, adherents of the flat Earth theory would need to identify a location on the planet where objects fall sideways rather than downwards.
The lunar phenomenon
In the hypothetical scenario of a flat Earth, complete with elephants and a turtle, the occurrence of a lunar eclipse would not result in a uniform shadow, but rather something resembling the image depicted below:

However, it is possible that this scenario is quite different from what actually happens.
Shadow Formation
If the Earth were flat, sunlight would cast shadows in a manner similar to a flashlight. In other words, objects of significant height located in the opposite direction of the Sun would remain in shadow even after sunset.
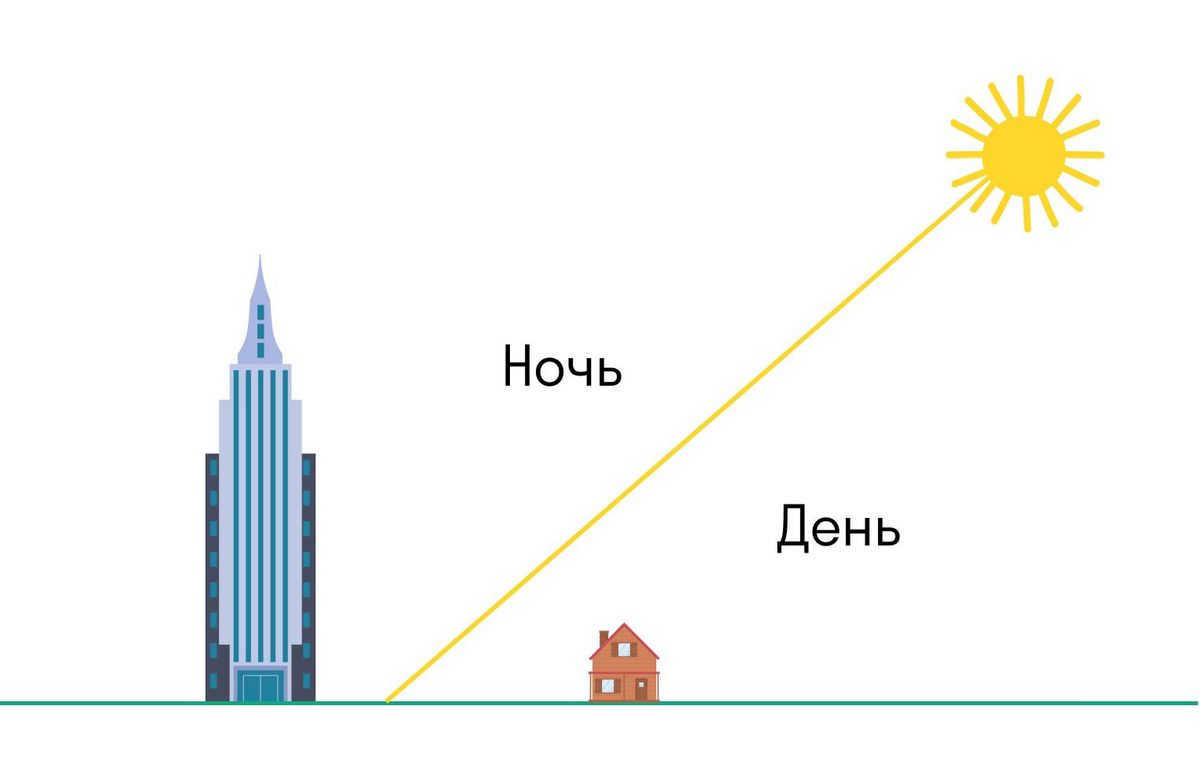
However, if the Earth were spherical, buildings or mountains would still receive sunlight even after the sun has set or before it has risen.
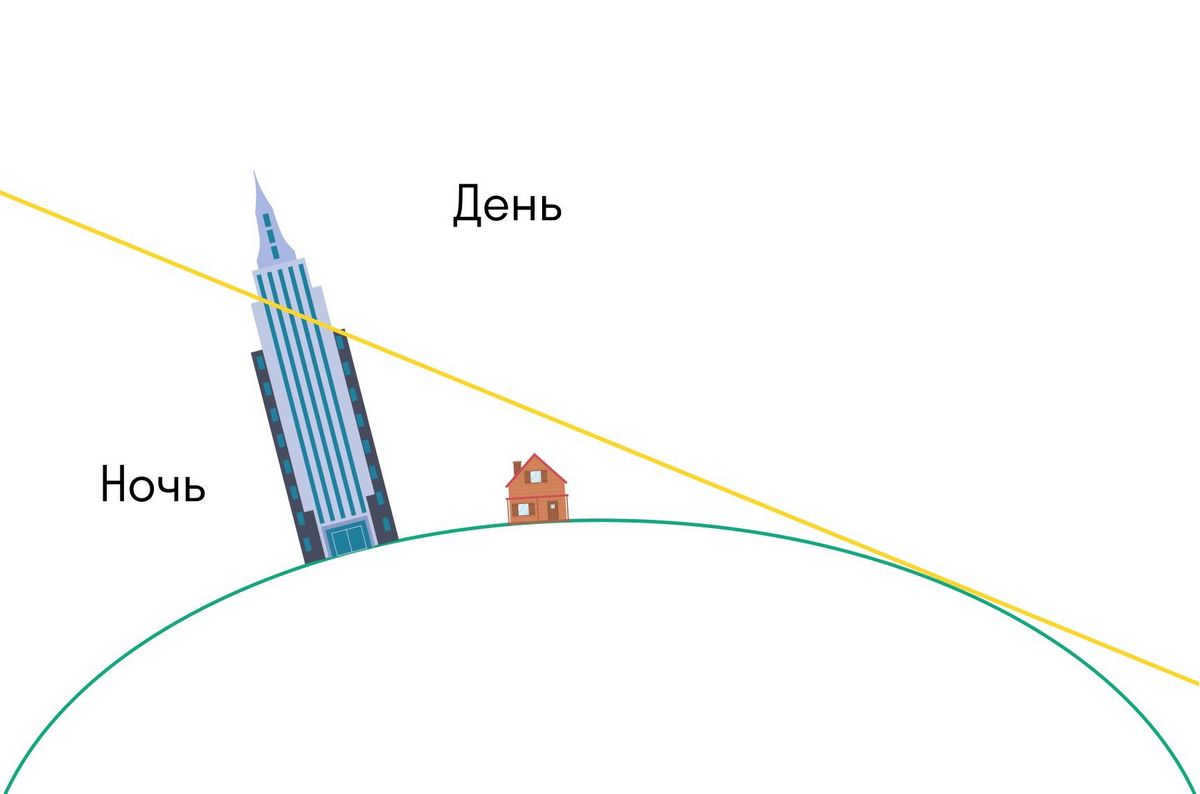
If you witness a sunrise or sunset in the mountains, or simply look at pictures, this is the breathtaking sight that awaits you.
It is now universally accepted that the Earth is not flat, but it cannot be described as a perfect sphere either – it is, in fact, an ellipsoid.
An ellipsoid is a shape that resembles a flattened ball with an elliptical cross-section. This is the precise shape that allows satellites to orbit along their elliptical trajectories.
Ellipse
Ellipse is a closed curve in the plane, representing a special instance of an oval shape. An ellipse possesses two axes of symmetry – one horizontal and one vertical – each composed of two semi-axes.
Furthermore, an ellipse exhibits two focal points, designated as points where the sum of distances from any given point P(x,y) remains constant.
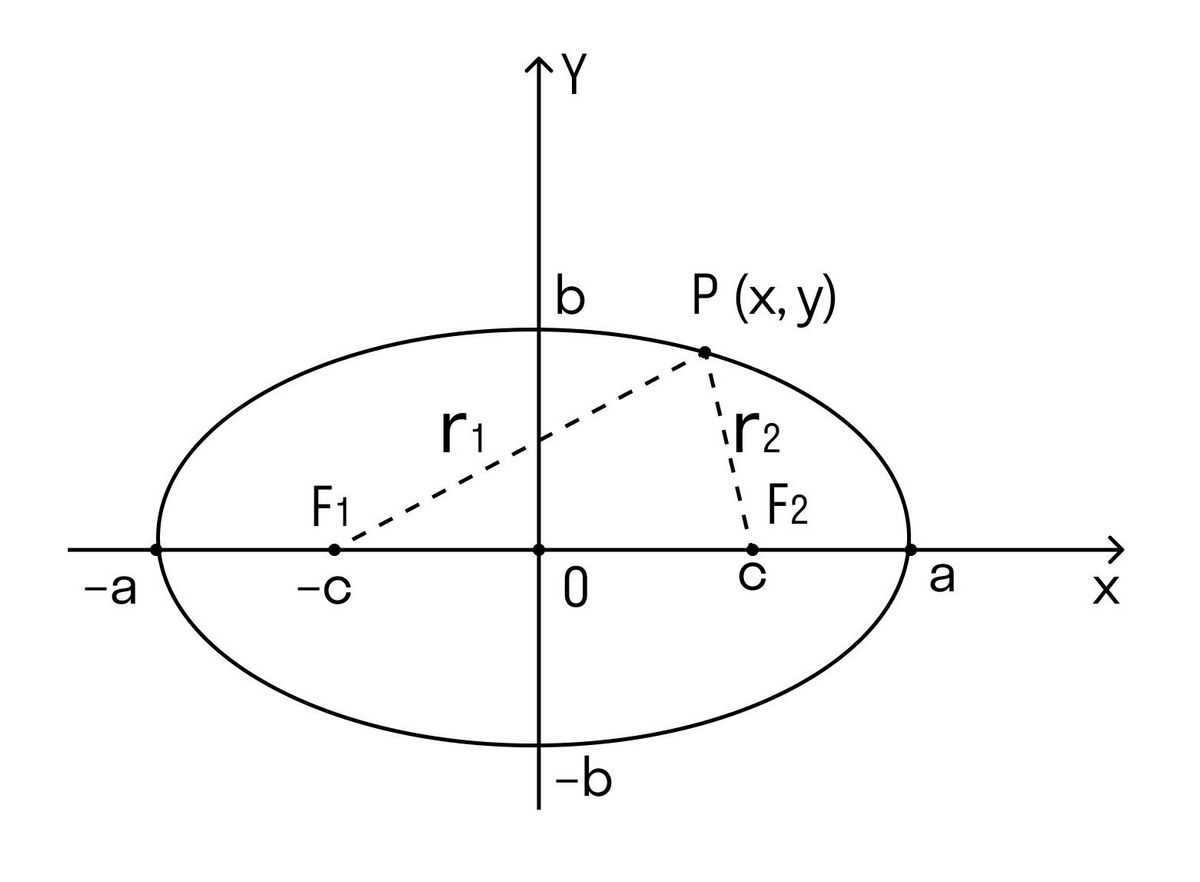
Now we have all the necessary knowledge to understand what Kepler’s laws entail.
Kepler’s First Law
Every planet within our solar system orbits the Sun along an elliptical path, with the Sun positioned at one of its foci.
The Sun occupies one of the focal points of the ellipse. The point B, which is closest to the Sun along the trajectory, is referred to as perihelion, while the point A, which is furthest from the Sun, is known as aphelion..
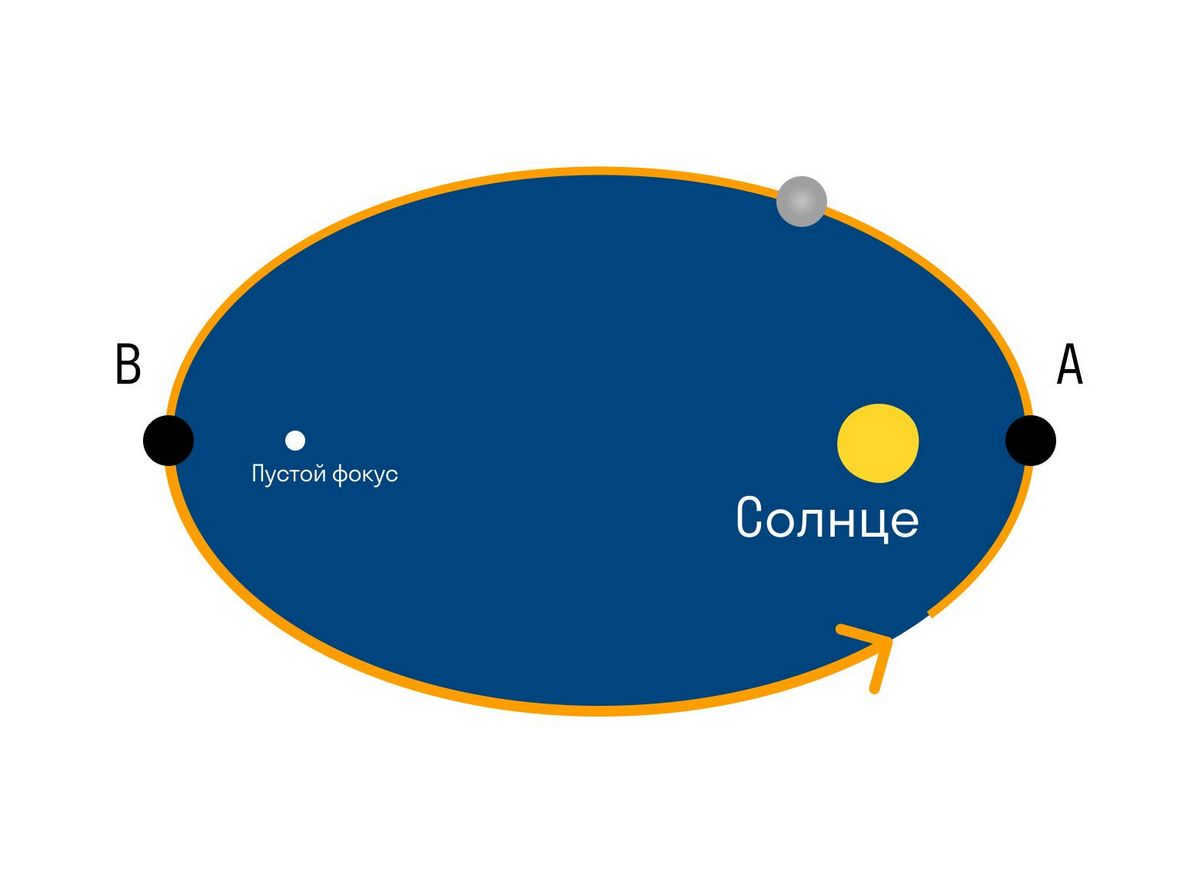

The first law formulated by Kepler is relatively simple, yet it holds significant importance as it greatly advanced the field of astronomy during its time. Prior to this groundbreaking discovery, astronomers were under the belief that planets moved exclusively in circular orbits. However, when observations began to contradict this notion, scientists resorted to adding small circles to the main circular motion that planets described around specific points within the main circular orbit. Kepler, armed with the extensive database of observations collected by Tycho Brahe, was able to transcend these outdated ideas through careful study and analysis.
Kepler’s second principle (the law of equal areas)
The planet’s radius vector sweeps out equal areas in equal times.
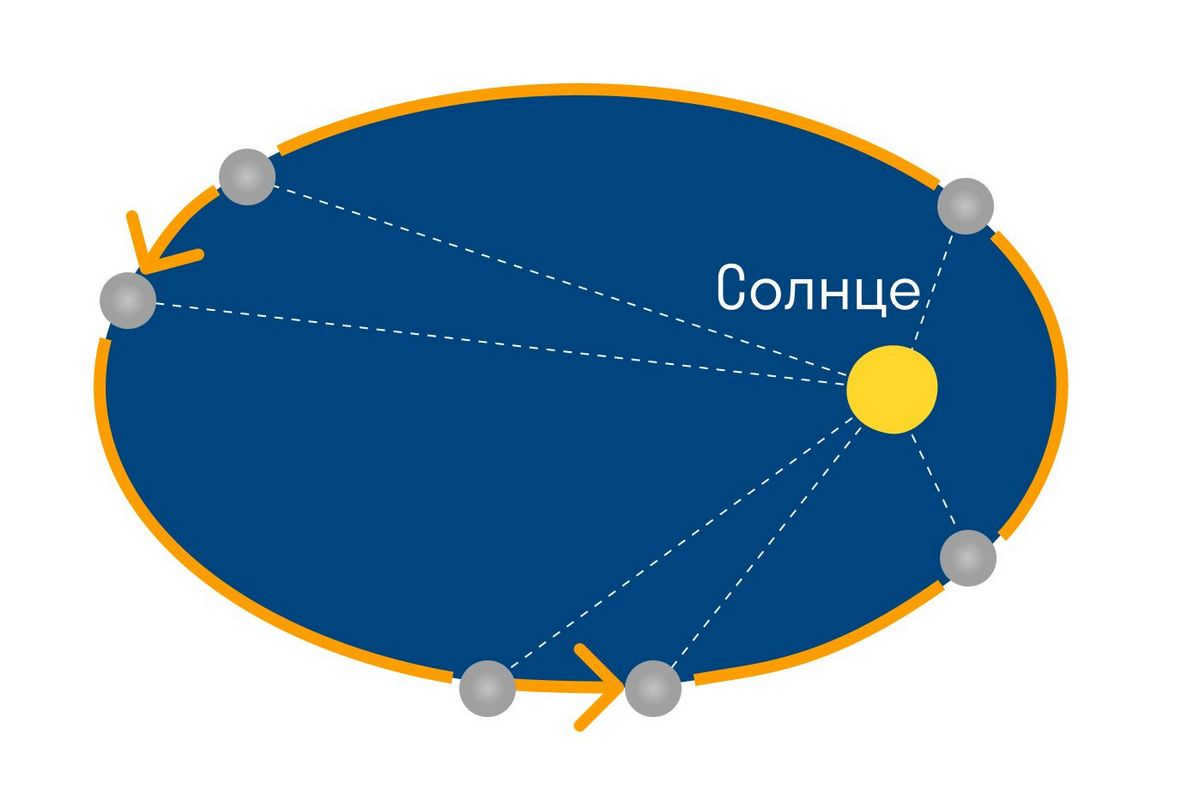
The movement of each planet follows a path that passes through the Sun’s center. Additionally, the line connecting the Sun and the planet covers equal areas in equal amounts of time. Consequently, celestial bodies do not move at a constant rate around the Sun: they reach their highest speed when closest to the Sun (perihelion) and their lowest when farthest away (aphelion).
This phenomenon is observable in the Earth’s movement. Every year, in early January, our planet reaches perihelion and accelerates in its orbit. This causes the Sun to appear to move faster along the ecliptic compared to other times of the year. Conversely, in early July, the Earth reaches aphelion and its orbital speed decreases, causing the Sun to appear to move slower along the ecliptic. As a result, summer days have longer daylight hours compared to winter days.
Kepler’s Third Law
The relationship between the squares of the orbital periods of the planets and the cubes of the major semi-axes of their orbits is described by Kepler’s third law.
Kepler’s third law establishes a connection between the orbital periods of planets and satellites orbiting the Sun and the average distance from the Sun to a planet or satellite. This law holds true for both planets and satellites, with an accuracy of less than 1%.
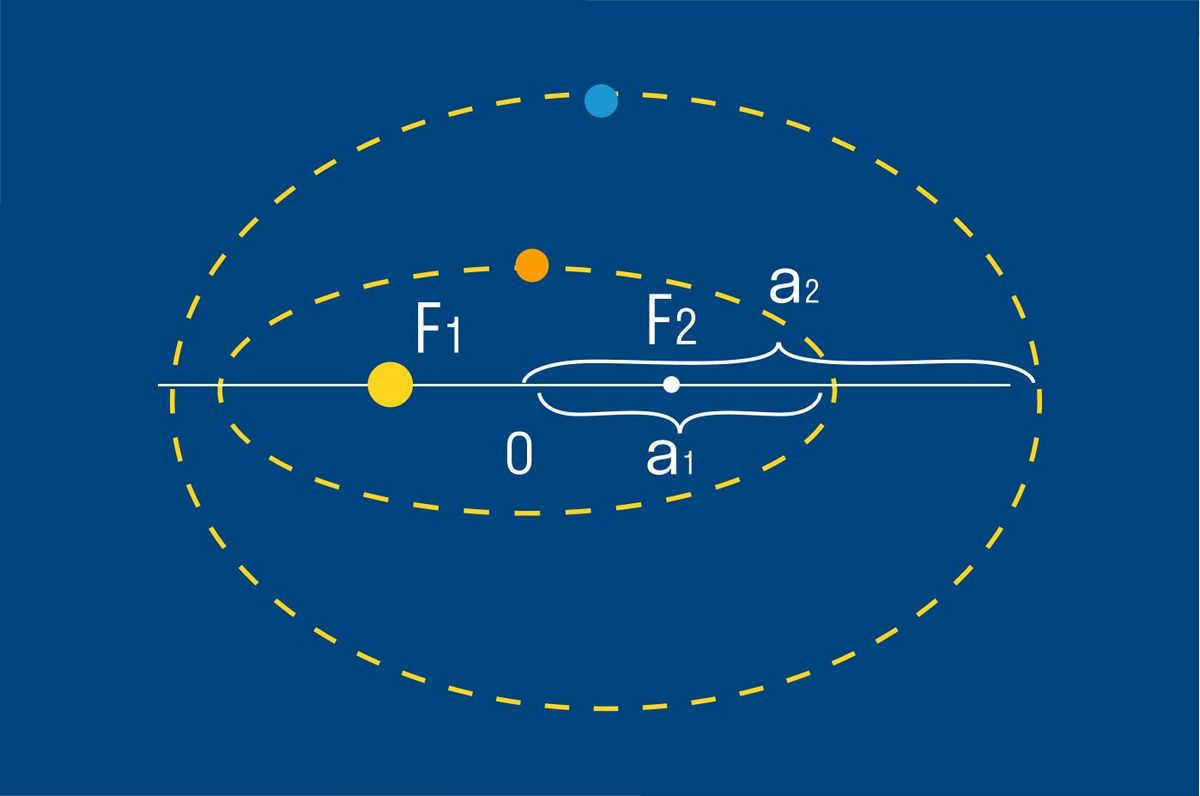
By applying this principle, one can determine the duration of a planetary year (the time it takes for a complete orbit around the Sun) by knowing the planet’s distance from the Sun.
The reverse is also possible – by knowing the period of revolution, one can calculate the orbit.
Kepler’s laws are based on observations and generalizations and were formulated by Isaac Newton in his Law of Universal Gravitation. The law states that all objects are attracted to each other, and the strength of this gravitational force is directly proportional to the masses of the objects and inversely proportional to the square of the distance between them.
This law can be represented by the following formula for the force of gravitation:
Newton was the first scientist to recognize that gravitational forces exist between any objects in space, and it is these forces that determine the motion of these objects.
The primary and secondary cosmic velocities
Kepler’s laws are not only applicable to the movement of planets and other celestial bodies within our solar system, but also to the movement of man-made satellites and spacecraft. In this scenario, the focal point is the Earth.
In Douglas Adams’ book series called “Hitchhiker’s Guide to the Galaxy,” it is mentioned that flying essentially means evading the Earth. If you were to zoom past the Earth and reach the initial speed required for space travel, which is 7.9 km/s, you would transform into an artificial satellite orbiting our planet.
An artificial satellite of the Earth is a vehicle that orbits the Earth in a geocentric orbit. In order for this to happen, the spacecraft must possess an initial velocity that is equal to or greater than the primary space velocity.





