Celestial sphere refers to an imaginary sphere with an arbitrary radius, which is used to project celestial bodies and solve various astrometric problems. It is centered around the observer’s eye, whether they are on Earth’s surface or in other points in space (such as the center of the Earth). For an observer on Earth, the rotation of the celestial sphere replicates the daily movement of the stars in the sky.
Every celestial body matches up with a specific point on the celestial sphere, where it is crossed by a line that connects the center of the sphere to the center of the body. When examining the positions and apparent movements of the celestial bodies on the celestial sphere, a particular spherical coordinate system is selected. The positions of the celestial bodies on the celestial sphere are calculated using celestial mechanics and spherical trigonometry.
Background
The concept of the celestial sphere has its roots in ancient times, originating from the visual perception of a dome-shaped vault encompassing the heavens. This perception arose from the observation that celestial objects, due to their immense distance, appear equidistant to the human eye, making it difficult to discern variations in their distances. Ancient civilizations interpreted this phenomenon as evidence of a tangible sphere encompassing the entire world, adorned with countless stars. Consequently, they regarded the celestial sphere as a fundamental component of the universe. As scientific knowledge advanced, this notion of the celestial sphere gradually diminished. However, the geometrical framework of the celestial sphere, developed and refined in antiquity, has persisted and continues to be utilized in the field of astrometry.
Characteristics of the heavenly sphere
Vertical line and associated principles
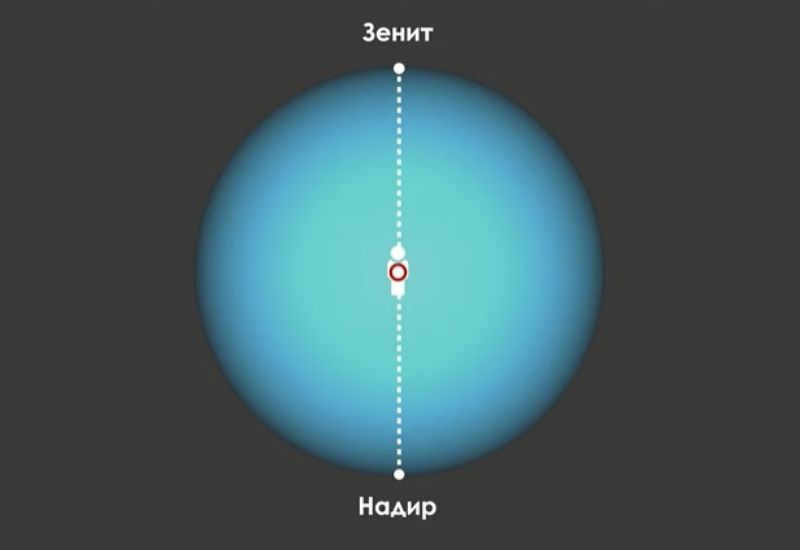
Vertical line – a direct line that extends through the middle of the heavenly sphere and a vantage point on Earth’s surface. The vertical line intersects the surface of the heavenly sphere at two points – the apex directly above the observer’s position and the nadir directly beneath the observer’s feet.
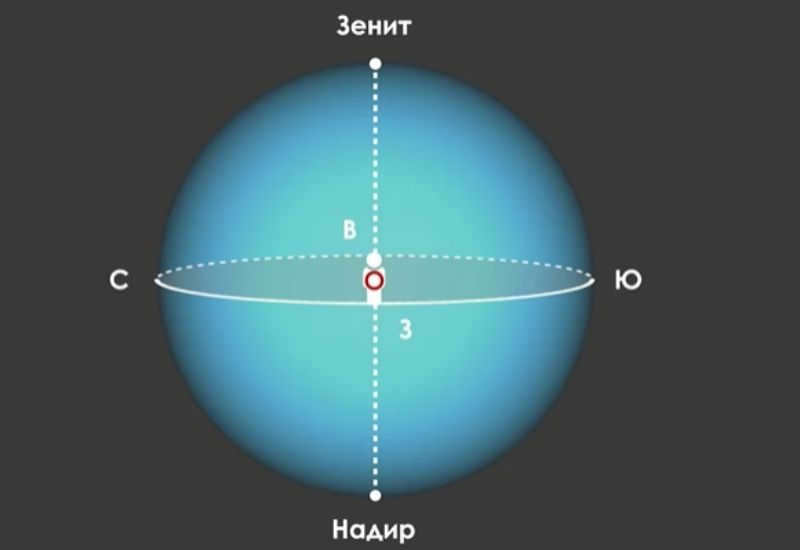
The authentic boundary – the grand circle of the celestial sphere whose plane is upright to the plumb line. The authentic boundary separates the exterior of the celestial sphere into two halves: the observable hemisphere with its peak at the zenith and the imperceptible hemisphere with its peak at the nadir. The authentic boundary does not match with the observable boundary due to the altitude of the observation spot above the surface of the earth, and due to the bending of light rays in the atmosphere.
The circle of altitude or vertical luminary – a significant semicircle of the celestial sphere that passes through the luminary, zenith, and nadir. Almukantarat (Arabic. “circle of equal heights”) – a minor circle of the celestial sphere, with a plane that is parallel to the plane of the mathematical horizon. The circles of altitude and almucantarates create a coordinate grid that determines the horizontal coordinates of the luminary.
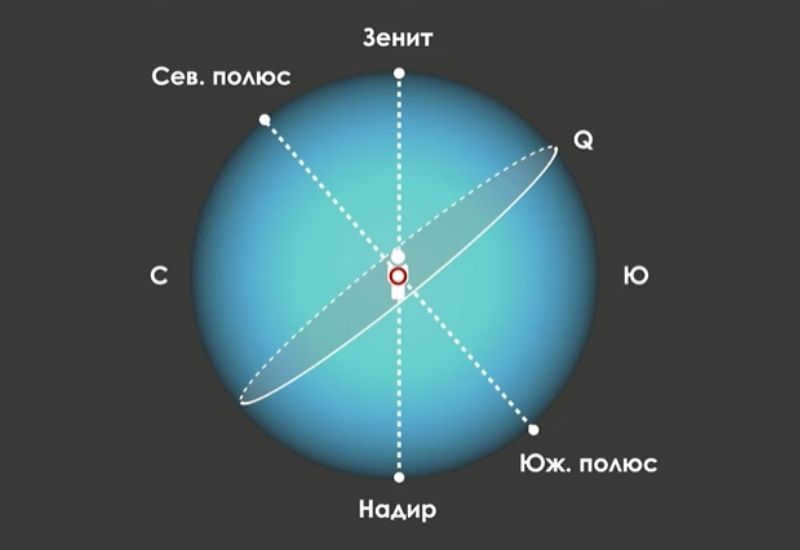
World axis – A hypothetical line that passes through the center of the Earth, around which the celestial sphere appears to rotate. The axis of the Earth intersects with the celestial sphere at two points – the North Pole and the South Pole. The rotation of the celestial sphere is counterclockwise around the North Pole, when observed from the inside.
The celestial equator – is a large circle on the celestial sphere, perpendicular to the Earth’s axis and passing through the center of the celestial sphere. The celestial equator divides the celestial sphere into two hemispheres: the Northern Hemisphere and the Southern Hemisphere.
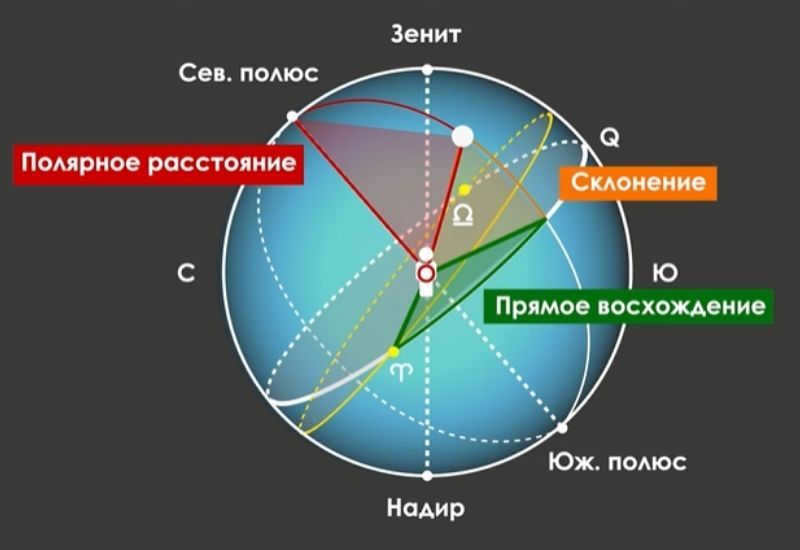
Circle of declination – the great circle on the celestial sphere that passes through the Earth’s poles.
Daytime parallel – a small circle on the celestial sphere that is parallel to the celestial equator. The apparent daily movements of celestial bodies occur along daytime parallels. The circles of declination and daytime parallels create a coordinate grid on the celestial sphere that determines the equatorial coordinates of the celestial bodies.
Terms originating from the intersection of the concepts “Plumb Line” and “Rotation of the celestial sphere”
The celestial equator intersects with the mathematical horizon at both the eastern point and the western point. The eastern point is where the points of the rotating celestial sphere emerge from behind the horizon. The semicircle of altitude that passes through the eastern point is known as the first vertical.
Celestial meridian – the great circle of the celestial sphere whose plane intersects with the plumb line and the axis of the world. The celestial meridian divides the surface of the celestial sphere into two hemispheres: the eastern hemisphere and the western hemisphere.
Noon Line – the line where the celestial meridian intersects with the mathematical horizon. This line intersects the mathematical horizon at two points: the northern point and the southern point. The northern point is the one that is closer to the North Pole.
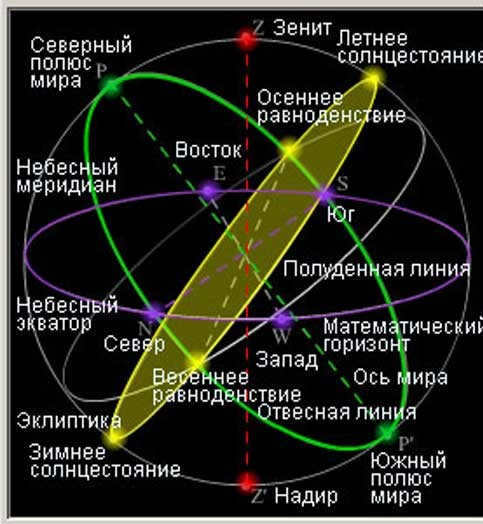
The yearly motion of the Sun on the celestial sphere and associated ideas
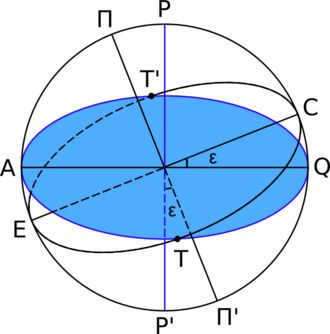
P,P’ – geographical poles, T,T’ – equinox points, E,C – solstice points, P,P’ – poles of the Earth’s orbit, PP’ – Earth’s axis, PP’ – orbit axis, ATQT’- equator, ETCT’ – ecliptic
Ecliptic – the major circle of the sky, where the Sun’s apparent annual motion takes place. The ecliptic plane intersects with the celestial equator at an angle ε = 23°26′.
The equinox points, where the ecliptic intersects the celestial equator, are known as the vernal equinox and the autumnal equinox. During the vernal equinox, the Sun moves from the southern hemisphere of the celestial sphere to the northern hemisphere, while at the autumnal equinox, it moves from the northern hemisphere to the southern hemisphere. The solstice points, located 90 degrees away from the equinoxes, are the farthest from the celestial equator. The summer solstice point is in the northern hemisphere, while the winter solstice point is in the southern hemisphere. These four points are represented by zodiac symbols, which correspond to the constellations they were in during Hipparchus’ time (although they have shifted due to precession). The spring equinox is associated with the sign of Aries (♈), the autumn equinox with the sign of Libra (♎), the winter solstice with the sign of Capricorn (♑), and the summer solstice with the sign of Cancer (♋).
The axis of the ecliptic refers to the line that runs perpendicular to the ecliptic plane on the celestial sphere. This axis intersects with the celestial sphere at two distinct points – the northern pole of the ecliptic, which is situated in the northern hemisphere, and the southern pole of the ecliptic, which is located in the southern hemisphere. The northern pole of the ecliptic can be found at equatorial coordinates R.A. = 18h00m, Dec = +66°33', and is positioned in the constellation Draco.
The circle of ecliptic latitude, also known as the latitude circle, is a large semicircle on the celestial sphere that passes through the poles of the ecliptic.
Fascinating trivia
The term “zenith” has its roots in Arabic, where it is pronounced “zamt”. When transcribed into Latin letters as “zamt”, it was later misinterpreted by scribes as “zanit” and eventually became known as “zenith”.
Additional information
Important details
- ↑Levitan E. Uncommon celestial occurrence // Science and Life. – 1988. – № 9. – p. 116.
- ↑Tsesevich V.P. Ecliptic // What and how to observe in the sky. – 6th ed. – M.: Nauka, 1984. – pp. 48-49. – 304 p.
Literature
- I. N. Veselovsky wrote about the Astronomy of the Orphics in the journal Questions of the History of Natural Science and Technology. This article was published in Moscow in 1982 and it is the second issue, pages 120-124.
- S. V. Zhitomirsky explored the Antiquity of celestial circles in the journal Earth and the Universe. This article was published in 1998 and it is the third issue, pages 31-36.
- G. P. Matvievskaya discussed Spherics and Spherical Trigonometry in Antiquity and in the Medieval East in the book Development of Methods of Astronomical Research, Vyp. 8. This book was published in Moscow and Leningrad in 1979.
| Newton’s laws – Law of universal gravitation – Kepler’s laws – Two-body problem – Three-body problem – N-body gravitational problem – Bertrand’s problem – Kepler’s equation |
| Celestial coordinate systemGalactic – Horizontal – First Equatorial – Second Equatorial – Ecliptic – International Celestial Coordinate System – Spherical Coordinate System – World Axis – Celestial Equator – Direct Ascension – Declination – Ecliptic – Equinox – Solstice – Fundamental Plane. |
| Keplerian orbital elements: Eccentricity – Major semi-axis – Mean anomaly – Longitude of ascending node – Pericenter argument – Apocenter and pericenter – Orbital velocity – Orbital node – Epoch |
| Motion of the Sun and planets on the celestial sphere – Ephemerides Planetary configurations: opposition – quadrature – parade of planets – Culmination – Sidereal period – Orbital resonance – Rotation period – Preceding equinoxes – Synodic period – Convergence Eclipse: solar eclipse – lunar eclipse – saros – Methone cycle – Coverage – Passage – Libration – Elongation – Kozai effect – Yarkovsky effect – Janibekov effect |
| Space velocity: first (circular) – second (parabolic) – third – fourth Tsiolkovsky’s formula – Gravitational maneuver – Goman trajectory – Osculating element method – Tidal acceleration – Change of orbital inclination – Docking – Lagrangian points – Pioneer effect |
| Geostationary orbit – Heliocentric orbit – Geosynchronous orbit – Geocentric orbit – Geo-transition orbit – Low reference orbit – Polar orbit – Tundra orbit – Sun-synchronous orbit – Lightning orbit – Oscillating orbit |
Wikimedia Foundation. 2010.
Celestial, also known as spherical astronomy, examines the position and observed path of stars on the celestial sphere.
Spherical astronomy utilizes spherical trigonometry and celestial mechanics to compute celestial coordinates.
Definition of the celestial sphere
The celestial sphere is an imaginary sphere with an arbitrary radius, upon which astronomical objects can be projected. The observer’s eye is considered to be the center of this sphere, and the observer’s location can be assigned to any point on Earth, either on the surface or at the center. The movement of the celestial sphere as perceived by the observer displays the daily motion of stars in the sky.
All luminous objects in the sky have a specific point where a ray passes through, connecting the center of the celestial sphere and the celestial body. The examination of the position and trajectory of stars is conducted using spherical coordinates.
The concept of the celestial sphere emerged centuries ago, rooted in the visual perception of the sky’s dome-like shape. This perception arises due to the fact that the distance to all stars is perceived as equal by observers on Earth.


Figure 1: An ancient understanding of the celestial sphere. Author24 – An Online Student Paper Exchange
Components of the celestial sphere
Vertical line. The line that passes through the center of the celestial sphere and is parallel to the plumb line, which originates from the observer’s position, is known as the vertical line. The points where it intersects the surface of the celestial sphere are known as the zenith (above the observer) and nadir (below the observer).
Horizon circle. The largest circle on the celestial sphere that is perpendicular to the vertical line is called the true (astronomical or mathematical) horizon. It divides the surface of the celestial sphere into two hemispheres: the visible hemisphere (with the zenith as the top) and the invisible hemisphere (with the nadir as the top).
The vertical (circle of altitude) of the star is the large semicircle that passes through the object, as well as through the nadir and zenith. The small circle, with a plane parallel to the horizon, is called almukantarat by the medieval Arabs, which means the circle of equal heights.
The axis of the world is the virtual straight line that intersects the center of the world (the imaginary axis around which the sphere of heavens rotates). This axis intersects with the spheroid of heavens, giving us the northern and southern world poles.
The celestial equator is the great circle that passes through the center of the heavens in a plane perpendicular to the world axis. This Great Circle divides the sphere of the heavens into northern and southern hemispheres.
The circle that touches the poles of the world and the star is known as the “circle of declination”. The term “diurnal parallel” is used to describe a small circle that is parallel to the equatorial plane.
These terms are used to describe the daily movement of the celestial sphere.
The points where the equatorial line and the astronomical horizon intersect are called the east and west points. The altitudinal semicircle that passes through the east point is known as “the first vertical”.
The celestial meridian is the great circle that touches the plumb line and the world axis. It divides the celestial spheroid into eastern and western hemispheres.
The intersection of the celestial meridian and the astronomical horizon forms a straight line known as the noon line. This noon line intersects the astronomical horizon to establish the north and south points.
These concepts encompass the vertical line and the rotation of the celestial sphere.
Furthermore, we have terms related to the yearly path of the Sun.
The ecliptic refers to the great circle on the spheroid where the annual course of the Sun is observed.
The points of the vernal and autumnal equinoxes are designated as the intersections of the ecliptic and the celestial equator. The equinox points are connected by a straight line known as the line of equinoxes. The summer and winter solstice points are located on a line perpendicular to the equinox line. The ecliptic axis is the diameter of the celestial sphere that is perpendicular to the ecliptic plane. The ecliptic curve has both a north and south pole.
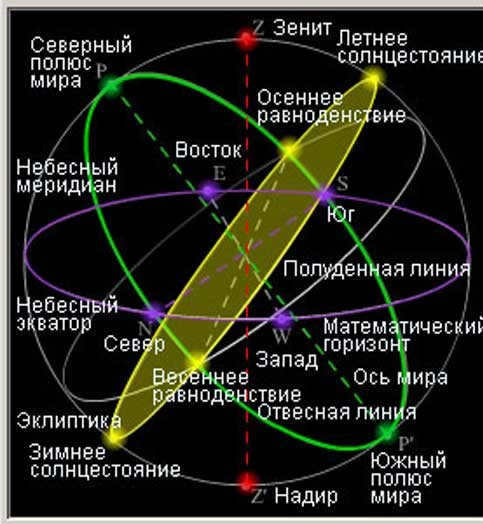
Figure 2: Elements of the celestial sphere. Author24 – Online Student Paper Exchange
Celestial mechanics
Celestial Mechanics is a field of astronomy that utilizes the principles of classical mechanics to analyze and compute the movement of celestial bodies (primarily the solar system) and phenomena associated with this motion.
Celestial mechanics is distinguished by its adherence to Newton’s and Kepler’s laws.
- The law of inertia. This principle states that in a reference frame with zero acceleration and no external influences, all objects either remain at rest or move in a straight line at a constant velocity.
- The principle of force. When a force is applied to an object, it causes the object to undergo accelerated motion, with the acceleration being greater when the force applied is greater.
- The principle of reaction. According to this principle, the interaction between objects occurs through forces that are equal in magnitude but have opposite directions.
- Principle #1. For planets, their characteristic trajectory of motion is a closed curve in the shape of an ellipse. In this case, the location of the Sun serves as one of the foci of the ellipse. Each orbit has two foci, which are a pair of points within the elliptical orbit located at fixed distances from it.
- Principle #2. The velocities of the planets are highest when they are located at the closest distance to the Sun and lowest when they are located at the farthest distance (perihelion and aphelion).
- Law #3. The relationship between the squared period of complete orbit passage and the cube half-axis of the orbit is stated.
Spherical trigonometry
Spherical trigonometry is the branch of trigonometric science that studies the relationship between angular magnitudes and the size of the sides of geometric figures known as spherical triangles.
The ancient Greek scientist Hipparchus is considered the “founding father” of this branch of trigonometry. Other notable contributors to the development of spherical trigonometry include Claudius Ptolemy and Menelaus of Alexandria.
The establishment of spherical trigonometry as a distinct scientific discipline occurred when the mathematical works of Muslim scholars during the Middle Ages emerged. Among them, noteworthy contributors to the advancement of spherical trigonometry include Ibn Irak, Sabit ibn Korra, Abu-l-Wafa, Kushyar ibn Labban, and others. These individuals introduced key mathematical operators, formulated and substantiated the spherical sine theorem, and made several other significant discoveries.
Subsequent progress in spherical trigonometry can be attributed to the works of renowned scientific luminaries such as Regiomontanus, Mavrolico, and Copernicus.
In this article, you will discover the fundamentals of the celestial sphere, its intricate organization, the significance of the plumb line and its associated concepts, the mechanics behind diurnal rotation, as well as the various spherical coordinate systems. Additionally, you will gain insight into how the perspective of the starry sky evolves with the changing seasons, the time of day, and your geographical location.
What is the Celestial Sphere?
In the past, it was believed that the Earth was a flat disk and that all celestial bodies orbited around it within a celestial dome. However, with the advancements in space exploration, it is now unquestionable that the Earth is a sphere. Nonetheless, the idea of a dome has been replaced with the concept of the “celestial sphere”.
The celestial sphere is an infinitely large sphere onto which all visible stars are projected. At the center of this sphere is an observer, whether they are on Earth or aboard a space station. This projection simplifies the solution of astronomical problems.
The celestial sphere is a representation of all the objects in space projected onto the Earth’s surface. Astronomers often use various coordinate systems to solve different problems, but they all share similarities. Spherical astronomy is the scientific field that studies the arrangement of stars on the celestial sphere. It encompasses specialized branches of mechanics and trigonometry that were specifically developed to work with the surface of a sphere, rather than flat planes like most trigonometric sciences.
Characteristics of the heavenly sphere
The heavenly sphere encompasses not only the positions of all the celestial bodies, but also numerous points of reference that scientists can accurately identify, quantify, and forecast the movement of the stars. It is crucial to understand that in the majority of calculations, the sphere is simply a visual representation that symbolizes many of the agreed-upon principles expounded upon in the following passages.
Plumb line and associated ideas
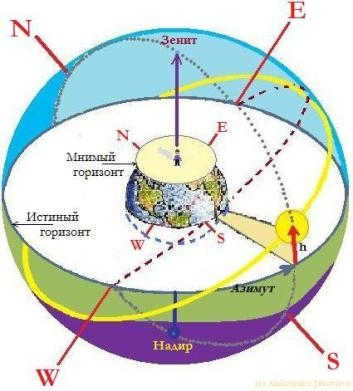
A plumb line, which is also referred to as a vertical line, represents an axis that aligns with the position of the string of an imaginary pendulum (plumb line) situated at the center of the sphere. This line intersects the sphere at two specific points: directly above the observer’s head (known as zenith) and below their feet (known as nadir). It serves as the primary axis of the celestial sphere within the horizontal coordinate system.
The astronomical horizon, also known as the true horizon, is a significant circle on the celestial sphere. It is defined by a plane that is perpendicular to the plumb line. This circle divides the celestial sphere into two equal parts: the visible hemisphere above the observer and the invisible hemisphere below. It is important to note that the true horizon observed from the ground may not coincide with the visible horizon. This discrepancy is caused by the curvature of light and the fact that the observer is located above the Earth’s surface.
To navigate the celestial sphere, it utilizes its own coordinate system, which differs from the traditional Cartesian grid. Instead of using x and y axes, it employs circles of altitudes and almucantarats.
A circle of altitudes is a plane that intersects the astronomical horizon perpendicularly and passes through the zenith, nadir, and celestial bodies. On the other hand, an almucantarat is a plane that runs parallel to the true horizon. The point where these planes intersect the celestial sphere determines the spherical coordinates of the celestial bodies.
Rotation of the Celestial Sphere and Related Concepts on a Daily Basis
The axis of the globe resembles the Earth’s rotational axis, running through the north and south poles of the globe, which may not coincide with the zenith and nadir points. The celestial sphere rotates around this straight line in a strictly counterclockwise direction.
Similar to the Earth’s equator, the celestial equator is a line that divides the sphere into two equal parts – the northern and southern hemispheres. Perpendicular to the axis of the globe, the celestial equator passes directly through the center of the sphere.
The path of the luminary is represented by a circle on the celestial sphere, indicating the movement of the Sun. This circle traverses both hemispheres and the point where the celestial body is positioned.
The daily parallel is the circle of the celestial sphere on which the luminary travels each day. In the northern hemisphere, all observed luminaries move counterclockwise on this circle, while in the southern hemisphere, they move clockwise.
When combined, the circles of the luminaries and the diurnal parallels create a coordinate system known as the equatorial coordinate system.
Words associated with the idea of the plumb line and the rotation of the sky sphere
Due to the fact that the celestial equator and the actual horizon are both circular, they only intersect at two points. These points are known as the west and east points. The celestial bodies always appear to rise from the horizon close to the east point and set near the west point.
Another plane, known as the celestial meridian, runs parallel to the plumb line and the Earth’s axis. It divides the sphere into two halves – the eastern hemisphere and the western hemisphere.
The celestial meridian intersects with the true horizon to form a straight line known as the noon line. This line creates two additional points on the celestial sphere: the north point, which is located closer to the north pole, and the south point, which is located closer to the south pole.
The yearly movement of the Sun across the sky
The Sun’s path across the sky is known as the ecliptic, and it follows a circular trajectory that is inclined at an angle of 23 degrees from the celestial equator.
During the equinoxes, the ecliptic intersects the celestial equator. These points are referred to as the spring and fall equinox points because they mark the Sun’s transition from the northern hemisphere to the southern hemisphere and vice versa. The two equinox points are connected by an imaginary straight line that passes through the center of the celestial sphere, known as the equinox line.
If a straight line is drawn from the center of the equinox line perpendicular to the plane of the celestial equator, it will indicate two significant points on the celestial sphere – the summer and winter solstices.
Typically, on diagrams and models, the equinoxes and solstices are denoted by zodiacal symbols corresponding to the constellations on the sphere:
- Spring Equinox – Aries;
- Autumnal equinox – Libra;
- Winter Solstice – Capricorn;
- Summer Solstice – Cancer
Spherical coordinate systems
When dealing with the celestial sphere, using the traditional three-dimensional coordinate system can be problematic. To address this issue, a specialized system of celestial coordinates was developed, allowing astronomers to accurately record and describe the positions of observed celestial bodies. These coordinates are defined by two arcs, while the third coordinate, which represents the distance to the object, may not always be known.
The use of spherical coordinate systems dates back approximately 2500 years. Euclid was the first to document the behavior of geometric figures and their interactions on the surface of a sphere. His findings were later adopted by physicists and astronomers worldwide, giving rise to what is now known as “Euclidean geometry.”
System for Determining Horizontal Coordinates
The horizontal coordinate system is commonly employed to ascertain the location of celestial bodies in the sky when the center of the celestial sphere is situated on the Earth’s surface. This system permits the calculation of coordinates without the need for intricate computations and can be acquired by means of a basic telescope set in an azimuthal configuration. Because of its straightforwardness and extensive utilization, it is employed by the majority of astronomical software to document the positions of stars.

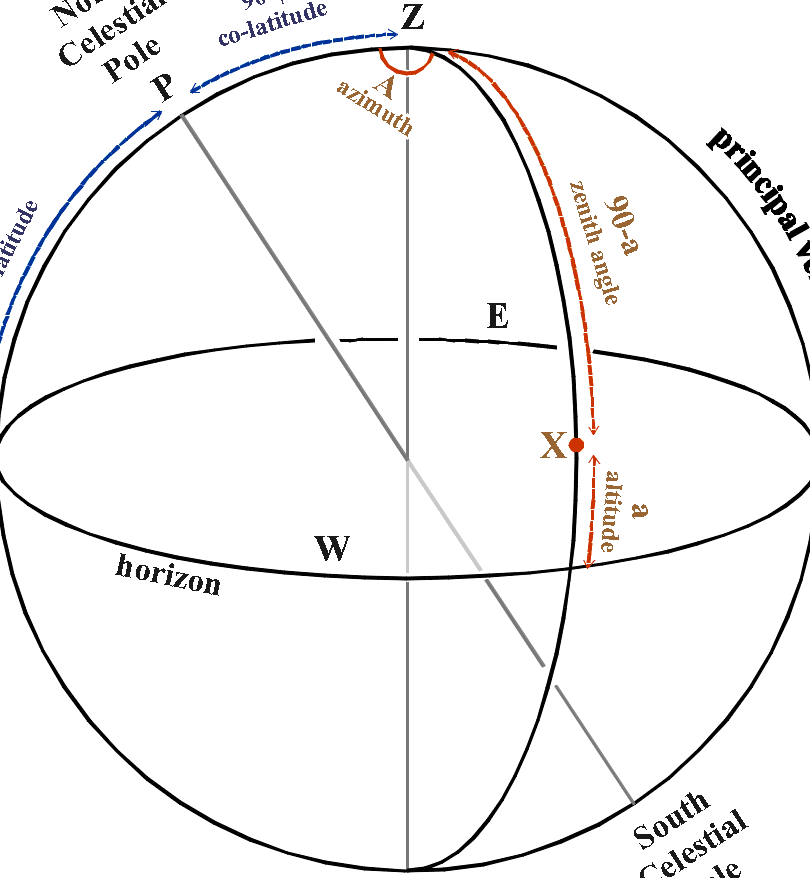
The horizontal coordinate system in astronomy is based on a reference point located at the center of the celestial sphere. It uses the plane of the true horizon as the reference. The first coordinate in this system is usually determined by either the altitude or the zenith distance of the desired point. The second coordinate is defined by its azimuth.
Now, let’s take a closer look at these terms:
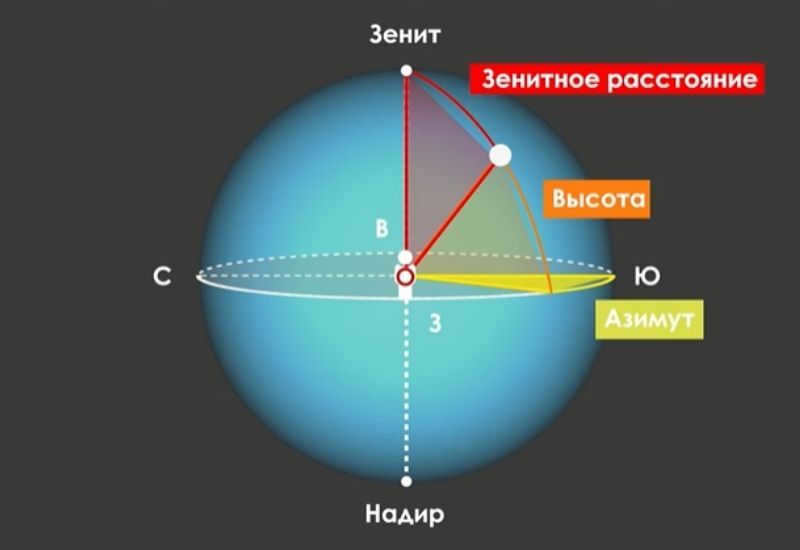
- Altitude (h) refers to the angle between the segments that connect the luminary to the center of the celestial sphere and the center of the celestial sphere to the point where the altitude line intersects the horizon. It is measured in degrees and ranges from 90 to -90.
- Azimuth (A) – The azimuth, denoted as A, refers to the angle of the arc that is drawn from the southern point to the circle of the luminary. This angle is always measured towards the west and is typically expressed in degrees ranging from 0 to 360. However, in certain scientific documents, it may be presented within the range of -180 to 180. It is important to note that the astronomical azimuth should not be confused with the navigational azimuth, as the latter is calculated with reference to the north.
The positions of the stars in the sky are always changing because the celestial sphere rotates. This rotation causes the measurements of the stars to change daily. However, certain measurements like declination and right ascension remain constant regardless of the sphere’s rotation. These measurements can only be affected by external forces.
Equatorial coordinate system #1
This method necessitates a specialized telescope arrangement known as an equatorial system. It is primarily utilized to ascertain the precise motion timing of celestial entities.
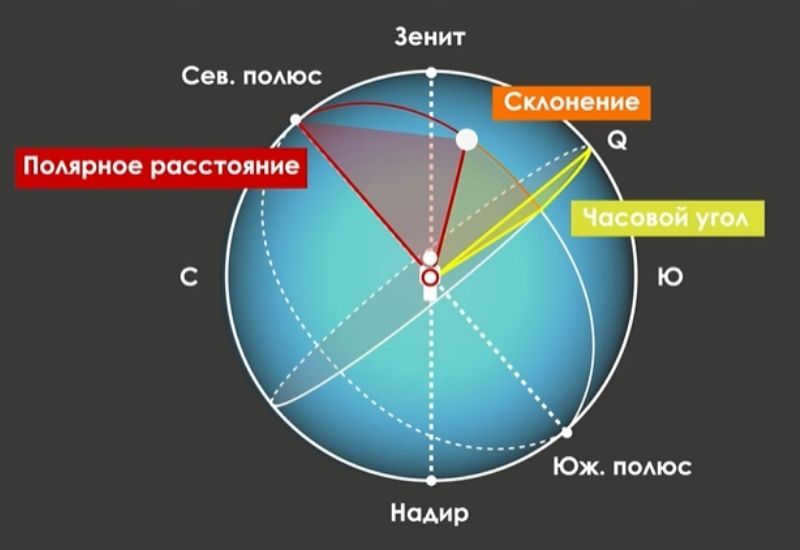
The celestial equator serves as the fundamental plane for this system. The first coordinate is determined by the declination or polar distance, while the second coordinate is indicated by the hour angle.
Declination represents the angle between the equatorial plane and a line connecting the center of the celestial sphere and the celestial body. Similar to altitude, it is measured in degrees ranging from +90 to -90. When a celestial entity moves through the zenith, its declination is always equal to the latitude of the observer’s location (the center of the celestial sphere).

The polar distance is the distance between the point of the North Pole and the celestial body. It is measured by the angle between the axis of the Earth and the point on the celestial sphere where the celestial body is located. The measurement is in degrees, ranging from 0 to 180 from the North Pole to the South Pole.
The hour angle is closely related to the declination coordinate. It represents the angle between the center of the celestial sphere, the point where the celestial equator intersects the meridian, and the point of declination. Various documents may present the measurements in degrees (ranging from 0 to 360) or in hours (ranging from 0 to 24). Additionally, there are reports that range from 180 to -180 degrees or from 12 to -12 hours.
Equatorial coordinate system #2
The Equatorial coordinate system #2 is the primary coordinate system used in astronomy. It not only allows for determining the location of individual stars but also enables the creation of highly accurate star maps. One of its main distinctions is its dependence on the point of the vernal equinox, which experiences changes in position over time. This characteristic is crucial for determining the epoch of the study. When analyzing data obtained in the past, it is necessary to apply parallax correction and calculate the coordinate of the vernal equinox point for the specific date in question.
Similar to the previous system, the Equatorial coordinate system #2 is based on the equatorial plane of the celestial sphere. However, instead of hour angles, it utilizes the coordinate of direct ascension.
The direct rise is the curve that connects the point of the spring equinox and the declination circle of the celestial body. In contrast to the other systems of coordinates, in the second equatorial coordinates are calculated in the opposite direction to the movement of the sphere. Similar to the angular distance, rise is also measured in degrees (0-60) and hours (0-4).
RA, which stands for Right Ascension, is a distinctive value within the equatorial coordinate system. It can be considered as the celestial counterpart to longitude. Similar to how longitude measures the angle along the Earth’s equator, RA measures the angle along the celestial equator, but relative to a specific point known as the prime meridian. This prime meridian corresponds to the closest point to the vernal equinox where the Sun intersects the celestial meridian.
The Ecliptic Coordinate System
The foundation of this coordinate system is the ecliptic plane, as suggested by its name.
The ecliptic latitude and ecliptic longitude are the primary coordinates in this system:
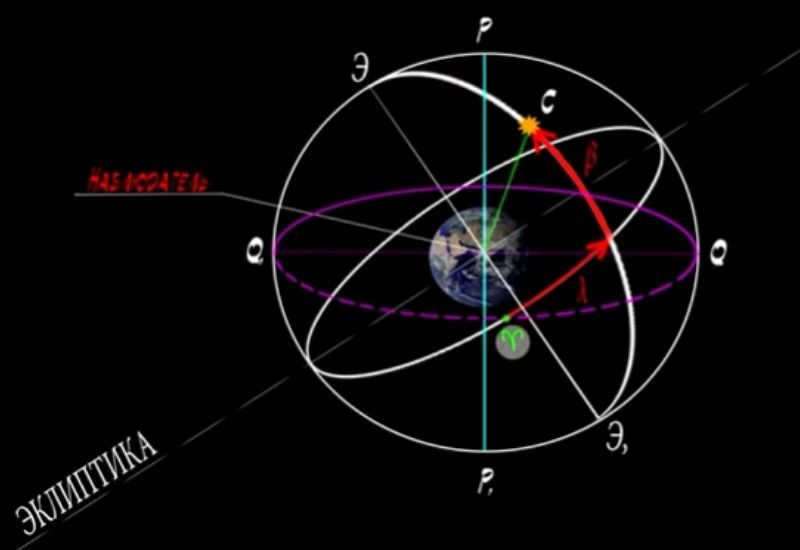
- Ecliptic latitude refers to the angle between the center of the celestial sphere, the ecliptic plane, and the point where the celestial body is marked. The latitude is measured from 90 degrees to -90 degrees, ranging from the north pole to the south pole.
- Ecliptic longitude is the angle between the circle of latitude and the segment from the center of the sphere to the point of the vernal equinox. Similar to other coordinate systems, it is measured in degrees, ranging from 0 to 360 in the direction of the sun’s motion on the sphere.
This particular coordinate system is primarily utilized for the study of celestial bodies within the solar system. Its main purpose is to determine the orbits of planets and their satellites.
Modifying the perspective of the celestial sky based on location, time, and date
The movement of the celestial sphere is heavily influenced by the specific time, place, and vantage point of observations. For instance, if an observer is positioned directly at the zenith, the visible stars will remain constant and unchanged. They will continuously rotate around the zenith, with no stars appearing to rise or set beyond the horizon. This is why only one hemisphere of the sky is observable from each of the poles, while the stars from the other hemisphere remain concealed at all times.
On the equator, however, the situation is completely different. The stars on the celestial sphere constantly move here, and from the equator, you can see all the stars from both hemispheres. These stars move in a direction perpendicular to the horizon, opposite to the rotation of the earth.
However, the movement of the stars is not only influenced by the daily cycle of the planet. The Earth also orbits around the Sun, which also has an impact. The trajectory of the Sun’s movement across the sky slightly changes every day. Scientists have discovered that this change is equivalent to 4 angular seconds. With the planet’s rotation rate of 1ug.sec/min, it becomes evident that each day becomes either 4 minutes longer or shorter, depending on the hemisphere. For astronomers, this means that a sidereal day is 4 minutes shorter than a solar day.
Additionally, this implies that every evening the star groupings ascending in the heavens move from east to west by 4 arc seconds along with the sun. Consequently, each month the duration of the daytime alters by approximately 1.5-2 hours, and, the star groupings that were visible in the heavens, fully traverse the entire celestial sphere, making room for the next ones. Following a year, when the planet completes a complete orbit around the Sun, this pattern concludes and commences anew.
The celestial sphere is a conceptual sphere that represents space objects projected onto its surface. It has an arbitrary radius and is centered around the observer’s gaze. The observer can be located anywhere. The motion of the celestial sphere illustrates the daily movement of stars in the sky.
The key components of the celestial sphere include:
- Plumb line. This is the line where the center of the sphere intersects with the observer’s plumb line. It forms the zenith and nadir points;
- The astronomical horizon is the circle of the celestial sphere that is perpendicular to the vertical and creates a visible hemisphere at the zenith and an invisible one at the nadir.
- The vertical represents a semicircle that passes through the luminary and through the zenith and nadir on the sphere. A smaller semicircle parallel to the horizon is called almucantaratus.
- The world axis is an imaginary straight line that intersects the center of the Earth and creates the North and South poles.
- The celestial equator is a large circle with a plane perpendicular to the world axis. It divides the celestial sphere into the Northern and Southern hemispheres.
- The circle of declination of the luminary is a large circle that touches the star and the poles.
- The diurnal parallel is a small circle that runs parallel to the celestial equator.
- The points where the astronomical horizon and the celestial equator intersect are known as the east and west points.
- The first vertical, also known as the altitude semicircle, passes through the east point.
- The celestial meridian is a great circle that is tangent to the Earth’s axis and the plumb line. It divides the sphere into the western and eastern hemispheres.
- The noon line is a straight line that is formed by the intersection of the planes of the astronomical horizon and the celestial meridian. At the point where the noon line intersects the celestial meridian and the horizon, the north and south points are located.
- The ecliptic is the great circle on the spheroid along which the Sun’s annual path is observed.
- The vernal and autumnal equinoxes occur at the points where the ecliptic and the celestial equator intersect.
- The equinox line is a straight line that connects the two equinox points.
- The points of the summer and winter solstice are found on a line that is perpendicular to the equinox line.
- The ecliptic axis is a diameter of the celestial sphere that is perpendicular to the celestial plane.
Spherical coordinate systems
Horizontal coordinate system
This system utilizes the astronomical horizon and the vertical as the main circles, with the cardinal direction represented by the plumb line.
Figure 2: Representation of the horizontal coordinate system.
The vertical passing through the star is referred to as the vertical of the luminary. If the vertical intersects the astronomical horizon at points E and W, it is known as the first vertical. The height of the star, denoted by h, is the arc of the vertical from the horizontal plane to the object’s location.
The almucantaratus of a star refers to the almucantaratus that intersects the body of the star A.
The azimuth of a star represents the spherical angle between the observing meridian and the vertical at the meridian point.

Struggling to figure it out by yourself?
Consider seeking assistance from your instructors.
There are three approaches to computing azimuth in nautical astronomy:
- Circular, spanning from 0 to 360 degrees;
- Semicircular, ranging from 0 to 180 degrees;
- Quaternary, encompassing a range of 0 to 90 degrees.
Equatorial coordinate system No. 1
This system is based on the world axis as the principal direction, with the observational meridian and the celestial equator serving as the principal circles. An auxiliary circle, known as the sidereal parallel, is also utilized.
Figure 3: Equatorial coordinate system No. 1
The declination of a star, denoted as δ, represents the arc of the stellar meridian. Depending on whether the star is located in the northern or southern hemisphere, the declination can be either north or south. The polar distance is the arc of the stellar meridian between the pole and the star, ranging from 0 to 180 degrees. The hour angle of the star, denoted as t, refers to the spherical angle formed by the world pole and the observation meridian at noon.
Alternative representation of the Equatorial coordinate system
This particular method of representing celestial objects involves the use of direct ascension, which measures the arc from the vernal equinox to the stellar meridian along the celestial equator. In addition, the position is determined by the declination.
Take a look at Figure 4 for a visual depiction of this alternative Equatorial coordinate system.
Ecliptic coordinate system
The ecliptic coordinate system is based on the ecliptic axis as the main direction and the ecliptic Earth plane and the plane of the latitudinal circle of the vernal equinox point as the main circle. In this system, the position of a star is determined by its astronomical longitude and latitude, independent of the observer’s location and the rotation of the celestial sphere.
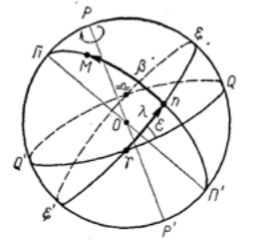
Illustration 5: Understanding the ecliptic coordinate system.

If you need assistance, consider seeking guidance from your instructors.
Home / Articles / Around Astrology / Astronomy for Astrologers. Part 2.
AROUND ASTROLOGY
Astronomy for astrologers. Part 2.
This is a continuation of the series titled “Astronomy for astrologers”. The series is divided into five parts, with this being Part 2.
1.4 The celestial sphere. Systems of celestial coordinates.
1.4.1 The celestial sphere.
The celestial sphere is a sphere with an arbitrary radius, centered at any point in space. It serves as a surface on which all the celestial bodies we observe in the sky are projected. In this case, we consider the Earth as the center of the celestial sphere.
Figure 1.5 depicts an imaginary celestial sphere. An observer is located at the center of the sphere, at point 0. The horizontal plane that passes through points O, Y, B, C, and 3 represents the horizon line, with points south, east, north, and west. The line SPM – JPM represents the axis of the world, which is an extension in space of the Earth’s axis of rotation.
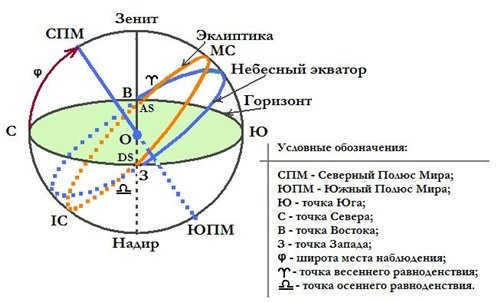
The World Poles refer to the locations where the world axis intersects with the celestial sphere. There are two points, with the first one being the North Pole of the World, where an imaginary observer would see the rotation of the celestial sphere in a clockwise direction. The second point is the South Pole of the World, which is opposite to the North Pole. The Polar Star is located near the North Pole of the World and is used by navigators and travelers for orientation purposes.
The Earth’s Axis is a hypothetical line that the Earth rotates around. For an observer on Earth, it appears as if the entire celestial sphere is rotating. The angle at which the Earth’s axis is tilted in relation to the horizon is equivalent to the geographic latitude of the observer’s location. The plane that is perpendicular to the Earth’s axis extends into space and aligns with the plane of the Earth’s equator. When this plane intersects with the celestial sphere, it forms a circle known as the celestial equator. The highest point of the celestial equator above the horizon is 90° minus the geographic latitude of the observer’s location.
The celestial meridian is the vertical plane that passes through points O, C, Y, as well as through the zenith and nadir.
The luminaries, as they make their way across the sky, first appear on the eastern horizon. As they reach the highest point in the sky, known as the celestial meridian, they are at their maximum height above the horizon. This is referred to as the upper culmination of the luminaries. After this, the luminaries begin to descend towards the western horizon. While they are still visible before setting, once they have set, they can no longer be seen. However, they continue their journey towards the celestial meridian on the northern side and cross it, which is known as the lower culmination. Eventually, the luminaries rise again on the horizon and begin their ascent on the following day. It is important to note that not all luminaries rise and set in this manner.
At various latitudes, we can witness different celestial phenomena, and if we take into account that the height of the North Pole is equal to the latitude of the observer’s location, it becomes clear how the daily movement of celestial bodies varies at different latitudes.
For instance, as the latitude increases, which means moving towards the north, the North Pole of the Earth will rise higher and higher above the horizon, while the celestial equator and daily parallels will intersect it at smaller and smaller angles. Consequently, the areas where celestial bodies do not rise or set will expand.
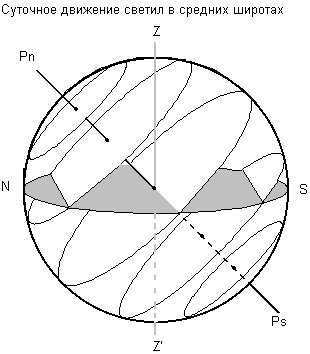
At this location, the North Pole of the Earth aligns with the zenith point, and the celestial equator aligns with the mathematical horizon. As a result, the diurnal parallels do not intersect with the horizon, meaning that all celestial objects in the northern hemisphere do not set (1*), while those in the southern hemisphere do not rise to their highest point (2*) (see Figure 1.6.). The altitude of these objects remains constant throughout the day, as it is equal to their declination. This is true for objects that are stationary relative to the celestial sphere, and as a result, they do not reach their highest point in the sky.
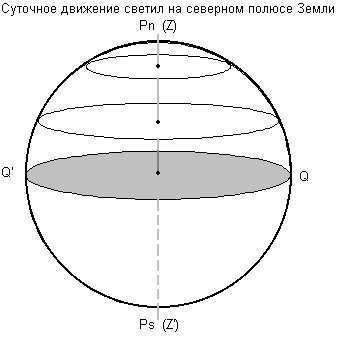
As you move towards the south, the height of the North Pole above the horizon decreases, and the celestial equator and daily parallels intersect it at a greater angle. This results in a decrease in the areas where the sun does not rise and where there is no daylight (see Figure 1.7.).
At the equator, the northern pole of the Earth aligns with the northern point, while the southern pole aligns with the southern point. The celestial equator, in turn, passes directly through the zenith. The diurnal parallels, which are perpendicular to the horizon, are split in half by it. There are no zones where luminaries do not rise or set – any luminary situated on the equator remains above the horizon for half of the day and below it for the other half (refer to Figure 1.8.).
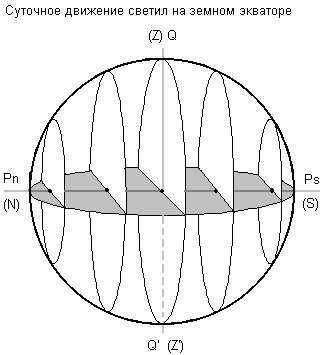
In astronomy, the celestial parallel, also known as the diurnal parallel, refers to a small circle on the celestial sphere that runs parallel to the celestial equator and intersects with a celestial body.
As one moves further southward, the scenario is similar to what has been described for moving northward, with the only difference being that in the southern hemisphere, the point where the celestial equator and the celestial meridian intersect is located north of the zenith, as opposed to south.
Astronomers have a stronger interest in the Sun, Moon, and planets as opposed to the stars. They follow the path of the ecliptic, which is then projected onto the celestial sphere and depicted as a circle. The ecliptic is tilted at an angle of 23°27' in relation to the celestial equator and intersects with it at the vernal and autumnal equinoxes. The section of the ecliptic that lies to the north (Gemini and Cancer) rises higher above the horizon than the celestial equator, while the section that lies to the south (Sagittarius and Capricorn) rises to a lesser extent (3*).
The planet Earth rotates on its axis, creating the illusion of the celestial sphere revolving around the world’s axis. Approximately every 4 minutes, at the moment of upper culmination, the celestial equator shifts by one degree, as does the ecliptic. In regions near the tropics, one degree of the ecliptic rises every 4 minutes, while in middle latitudes, the opposite is true.
Due to the inclination of the ecliptic relative to the celestial equator, the Signs of the Zodiac that move from south to north – specifically from the winter solstice to the summer solstice – rise rapidly. These signs are known as the Signs of Rapid Ascension, which include:
Capricorn, Aquarius, Pisces, Aries, Taurus, Gemini.
The opposite portion of the ecliptic has a gradual ascent, giving rise to its own unique set of Zodiac Signs known as the Signs of slow ascension. These Signs include: Cancer, Leo, Virgo, Libra, Scorpio, Sagittarius.
As the Sun moves through the Signs of rapid ascension, the length of the day increases, while in the Signs of slow ascension, the length of the day decreases. This phenomenon is reversed in the southern hemisphere.
To calculate the rising, culminating, and setting points of the ecliptic, one must determine the sidereal time and refer to the SMA (4*) table. To determine the position of a celestial body on the celestial sphere, one must consult the appropriate celestial coordinate system table.
Celestial coordinate systems are used to precisely define the location of celestial bodies on the celestial sphere.
The position of a point on the sphere can be uniquely determined by two independent coordinates. Since most luminaries appear as points to the observer’s eye, two coordinates from one of the celestial coordinate systems are enough to indicate their position: horizontal, equatorial, or ecliptic. Each celestial coordinate system is based on the two great circles of the celestial sphere. In astrology, the zodiacal coordinate system is commonly used, which is a variation of the ecliptic coordinate system but has some differences from the ecliptic system used in astronomy.
Here are some test questions:
1. What is the term used to describe the imaginary sphere surrounding the Earth called? 2. What are the names given to the two points on the Earth’s surface where its axis intersects? 3. What is the name of the imaginary line running through the Earth’s poles? 4. What are the terms used to describe the imaginary lines that divide the Earth into northern and southern hemispheres? What about the imaginary lines that divide the celestial sphere into northern and southern hemispheres? 5. What is the term used to describe the imaginary line passing through the North and South Poles and a given point on the celestial sphere? 6. Which celestial bodies are referred to as the non-ascending luminaries? What causes this phenomenon? Where is it observable? 7. What is the name of the imaginary line on the celestial sphere that is parallel to the Earth’s equator? 8. In approximately how many minutes does the position of the Sun change by one degree along the ecliptic? 9. Which zodiac signs are known as the signs of rapid ascension? What about the signs of slow ascension? 10. What are some celestial coordinate systems that you are familiar with?
1.4.2 The Horizontal Coordinate System
The horizontal coordinate system is utilized to ascertain the position of a celestial body in relation to the horizon at a specific geographical location.
In the realm of astrology, the horizontal coordinate system is frequently employed to determine the favorability or unfavorability of a particular place on Earth for an individual.
Let’s illustrate a vertical line ZZ’ (refer to figure 1.9.):
The uppermost point Z – zenith,
the lowermost point Z’ – nadir.
The celestial sphere encompasses a great circle, whose plane is perpendicular to the vertical line, which is referred to as the mathematical or astronomical horizon.
The primary line of the flat chart is the vertical line (ZOZ’), where Z is the lowest point, Z’ is the highest point), and its primary plane is the skyline but with the vertical line bent. Due to the compression of the Earth, the plane that touches the Earth’s surface does not align with the mathematical skyline. This plane is known as the geodetic skyline.
The coordinates that indicate the position of the luminary in the horizontal coordinate system: elevation (sometimes zenith distance) and azimuth.
Mathematical (true) skyline – the main circle of the celestial sphere (SWNE), the plane of which is perpendicular to the vertical line. The mathematical skyline divides the surface of the celestial sphere into two halves: visible to the observer with the zenith point Z, and invisible, with the nadir point Z’.
The mathematical horizon is positioned slightly higher above the visible horizon. It is elevated by approximately 2′,4 compared to the visible horizon. Moreover, the refraction of light within the Earth’s atmosphere slightly amplifies the apparent altitude of the celestial body, thereby causing the visible horizon to be further lowered relative to the mathematical horizon. The refraction at the horizon reaches a magnitude of 34′, which surpasses the observed diameter of either the Moon or the Sun.
Refraction – The phenomenon of light rays undergoing refraction as they traverse the Earth’s atmosphere. As a result of refraction, the apparent direction towards the celestial body differs from the true direction.
The measurement of the angle between the plane of the horizon and the direction to a celestial body Q is known as the altitude h (Fig. 1.9, 1.10.). When the celestial body is above the horizon, the altitude is considered positive, and when it is below the horizon, the altitude is considered negative.
For the horizon, the altitude is 0°,
for the zenith, the altitude is 90°,
and for the nadir, the altitude is -90°.
In order to establish the second coordinate, it is necessary to provide a point of reference on the horizon. This can be achieved by determining the north point (N) or the south point (S). Typically, the south point is chosen as the point of intersection between the horizon and the Sun’s vertical when the Sun is at its highest point above the horizon. Alternatively, the south point can be identified as the moment when the shadow cast by the Sun, in the plane of the horizon, is at its shortest length and aligns with the north-south direction.
One alternative is to establish the northern point as the point where the vertical projection of the Earth’s axis on the celestial sphere intersects with the horizon. The line that runs through the north and south points and lies in the horizon plane is known as the noon line. The west point W and east point E are positioned on a line that is perpendicular to the noon line. The east point is consistently located to the right of the north point N.
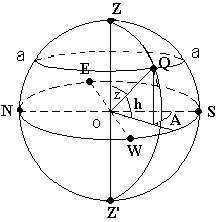
The celestial meridian is the great circle of the celestial sphere that passes through the zenith, north, and south points. It also includes the projections of the earth’s axis onto the celestial sphere, known as the north and south poles of the world. Another great circle that passes through the zenith, west, and east points is called the first vertical.
The zenith point (Z) and the nadir point (Z’) on the celestial sphere, which are analogous to the poles of the spherical coordinate system, have a declination (h) of +/- 90 degrees and an undefined azimuth. At the geographic poles, the concept of “sides of the world” does not apply, so the celestial meridian and azimuth are not defined there.
Test questions:
1. What is the celestial meridian?
2. What are the north and south poles of the world?
3. What is the first vertical?
4. Where are the zenith and nadir points located?
5. Why is the celestial meridian not defined at the geographic poles?
1. What is the name of the horizontal coordinate system? What is its purpose? 2. Which coordinates determine the position of a celestial body in the horizontal coordinate system? 3. How is the mathematical horizon defined? 4. How do you define refraction? 5. What do you call an almucantarate? 6. What is a vertical called? 7. What is an azimuth called? 8. In astrology, when is the horizontal coordinate system used?
1.4.3 Equatorial coordinate system.
The equatorial coordinate system is a celestial coordinate system that is derived from the celestial equator. There are two variations of this coordinate system: the first equatorial system and the second equatorial system.
Within astrology, the equatorial coordinate system is frequently utilized for forecasting events within specific cities, regions, and medical horoscopes.
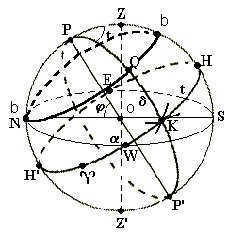
In the equatorial coordinate system. The primary axis is the axis of the world (ROP'), which goes through the poles of the world P (north) and P' (south) (Fig.1.11.).
The main plane is the plane perpendicular to it, which intersects the celestial sphere along the great circle HWH'E, known as the celestial equator.
Coordinates that determine the position of the celestial body in the equatorial coordinate system: in the first case – declination and hour angle; in the second case – declination and right ascension.
The celestial sphere is divided into two hemispheres – the northern celestial hemisphere and the southern hemisphere – by the celestial equator. The circle of declination, also known as the hour circle, is a great circle on the celestial sphere that passes through the luminary Q and the poles P and P’. This circle (PQP’) intersects the equator at point K.
Because the Earth’s axis of rotation is parallel to the world axis, the celestial equator is an extension of the Earth’s equator on the celestial sphere. This means that the equatorial coordinate system can be seen as a projection of geographic coordinates onto the celestial sphere.
The celestial equator intersects with the mathematical horizon at two points: the eastern point E and the western point W.
With respect to the horizon, the poles of the world and the celestial equator are positioned as follows:
The poles of the world are located in the plane of the celestial meridian because the celestial meridian is the projection of the plane of the terrestrial meridian onto the celestial sphere at the point of observation, and the latter represents the local north-south direction.
The distance between the world pole and the horizon is equal to the latitude of the observation point – this statement is sometimes referred to as the theorem of the height of the world pole.
The celestial meridian is a circle on the celestial sphere that is defined by the intersection of the plumb line and the world axis. It divides the surface of the celestial sphere into two hemispheres: the eastern hemisphere, represented by the east point E, and the western hemisphere, represented by the west point W. The celestial meridian intersects with the mathematical horizon at two points: the north point N and the south point S (the north point being closer to the north pole and the south point being closer to the south pole).
There are two points where the celestial meridian intersects with the celestial equator: the upper equatorial point H, which is nearer to the zenith point Z, and the lower equatorial point H’, which is nearer to the nadir point Z’. The planes of the celestial meridian and the mathematical horizon intersect on the line NS, which is referred to as the noon line.
When using the first equatorial system: the starting point is referred to as point H, which is where the celestial equator intersects with the celestial meridian (Fig. 1.11.). The angle between the plane of the celestial meridian and the circle of declination of the celestial body Q (or the length of the arc HK), which is measured in the direction of the celestial sphere’s rotation, specifically towards the west of point H, is known as the hour angle t. Since point H does not move during the daily rotation of the celestial sphere, the hour angle t of celestial body Q increases as time progresses, making it convenient to express it in terms of hours, minutes, and seconds. Typically, t is measured on both sides of the celestial meridian within the range of -12h to +12h.
In the second equatorial system: the reference point is taken as the vernal equinox point ( ^ ), which is one of the two points where the equator intersects with the ecliptic (see 1.4.4. below). It is important to note that the vernal equinox point remains fixed on the celestial sphere and undergoes daily rotation along with it, resulting in a varying hour angle proportional to time. The angular distance from the ^ vernal equinox point to the luminary’s declination circle Q (arc ^ K), measured counterclockwise against the rotation of the celestial sphere (i.e., east of ^ ), is referred to as the direct ascent and is represented by the letter (a) (Fig. 1.11.). For the world poles P and P’, neither the hour angle nor the direct ascent is defined. With this choice of the reference direction, the direct ascent of the point H also changes in proportion to time, so (a) is typically expressed in time units such as hours, minutes, and seconds, within the range of 0h to 24h. The hour angle of the vernal equinox point – the length of the arc H ^ in Fig. 1.11. – is known as the s sidereal time.
Test questions:
1. What is the name of the coordinate system that is known as the equatorial coordinate system? 2. How is the circle of declination defined? 3. What is the representation of the celestial meridian? 4. What is the point of reference for the 1st equatorial coordinate system called? And for the 2nd? 5. Which coordinates determine the position of the luminary in the 1st equatorial coordinate system? And in the 2nd equatorial coordinate system? 6. What is the definition of the luminary’s declination? 7. How is the hour angle defined? 8. What is the term for the direct ascent?
1.4.4 The ecliptic coordinate system
The coordinate system of the ecliptic is a celestial coordinate system that is based on the ecliptic (see Ecliptic coordinate system). Figure 1.12).
The primary plane in the ecliptic coordinate system is the projection on the celestial sphere of the plane of the Earth’s orbit, and the main axis is perpendicular to it (EE’).
The coordinates that specify the position of the celestial body in the ecliptic coordinate system are the ecliptic longitude and latitude.
The celestial sphere is intersected by the plane of the Earth’s orbit, creating a large circle known as the ecliptic. This circle represents the Earth’s yearly revolution around the Sun, with the Sun moving along the ecliptic in relation to the center of gravity of the Earth-Moon system. The ecliptic is denoted by the symbol (^ a g d).
Two points on the celestial sphere, known as the poles of the ecliptic, are intersected by a perpendicular line to the ecliptic plane. The north pole of the ecliptic (E) is located in the constellation Dragon and has equatorial coordinates α = 18h, δ = 90° – ε. The south pole of the ecliptic (E’) is located in the constellation of the Goldfish.
Because the earth’s equator is inclined to the plane of the earth’s orbit by an angle of ε ~ 23°26’5, the celestial equator, which is a continuation of the earth’s equator, is also inclined by the same angle ε. As a result, the ecliptic, which is the path of the Sun as seen from the Earth, intersects the celestial equator at two points: the vernal equinox point in the Pisces constellation (represented by the Aries symbol ^) (6*), where the Sun transitions from the southern celestial hemisphere to the northern hemisphere, and the autumnal equinox point in the Virgo constellation (represented by the Libra symbol d).
The ecliptic (astronomical) longitude of the luminary is the arc of the ecliptic from the point of vernal equinox (^) to the point of intersection with the circle of latitude of the luminary Q, counted in the opposite direction of the daily rotation of the celestial sphere, which is to the east. The point of vernal equinox is the point of reference on the ecliptic and in the equatorial system. Both latitude and longitude are typically measured in degrees.
The point on the ecliptic with λ = 90° and δ = + ε , is known as the point of the summer solstice. It is referred to as the point of the summer solstice and is represented by the symbol of the Cancer constellation ( a ). Currently, it is situated in the Taurus constellation. On the other hand, the point with λ = 270° and δ = – ε , is called the point of the winter solstice. This is known as the point of the winter solstice and is indicated by the Capricorn constellation sign ( g ). It can be found in the Sagittarius constellation.
Test questions:
1. What is the name of the coordinate system related to the ecliptic? 2. What serves as the reference point for the ecliptic coordinate system? 3. Which coordinates determine the position of the celestial object in the ecliptic coordinate system? 4. How is ecliptic longitude and latitude defined?
1. “Physics of Space,” a small encyclopedia published by the Soviet Encyclopedia Publishing House in Moscow in 1976.
2. “Physics of Cosmos,” another small encyclopedia published by the Soviet Encyclopedia Publishing House in Moscow in 1986.
3. “Philosophy of Physics” by Mario Bunge, published by Progress Publishing House in Moscow in 1975.
4. “Modern Concepts of Natural Science” by A.N.Babushkin, published in St. Petersburg in 2002.
5. “History of Calendar and Chronology” by S.I.Seleshnikov, published by Nauka Publishing House, Third Edition, Moscow, 1977.
6. The Mathematical Encyclopedia published by the “Soviet Mathematical Encyclopedia” Publishing House in Moscow in 1982.
7. Visit www.ipasoft.ru
8. Visit www.hea.iki.rssi.ru
9. Visit www.astrogalaxy1.narod.ru
10. Visit www.astronet.ru
(1*) In other cases, those who do not decline are the ones whose angular distance from the celestial equator (declination) is greater than 90° minus the latitude of the place where the observation is taking place.
(2*) The same rule applies to luminaries that do not set, but it should be noted that their declination is negative.
(3*) This applies specifically to the northern hemisphere.
(4*) Tables containing information about sidereal time, Meridians, and Ascendants are available.
(5*) It is important for the astrologer to understand this fact in order to avoid alarming people with predictions of a sudden shift in the Earth’s poles. It is crucial to differentiate between the geographical pole, the magnetic pole, and the Earth’s axis. Unfortunately, these concepts are sometimes misunderstood and confused.
(6*) A constellation refers to the actual (astronomical) position in the sky, based on the current understanding of the sky. On the other hand, a Zodiac Sign is a symbolic (now more astrological) designation. Once upon a time, constellations and Signs were aligned, but due to precession, they have diverged. However, the symbolism remains the same, even in the field of astronomy.