Ludwig Boltzmann (1844-1906) – an eminent physicist from Austria, renowned as one of the pioneers of molecular kinetic theory. Boltzmann’s contributions marked the emergence of molecular kinetic theory as a logically consistent and comprehensive physical theory. He provided a statistical explanation of the second law of thermodynamics and made significant advancements in the development and popularization of Maxwell’s electromagnetic field theory. With an innate fighting spirit, Boltzmann vigorously advocated for a molecular interpretation of thermal phenomena, facing off against scientists who denied the presence of molecules.
The equation (4.5.3) expresses the connection between the universal gas constant R and Avogadro’s constant NA. This proportion remains constant for all substances and is referred to as the Boltzmann constant, named after L. Boltzmann, a notable contributor to molecular kinetic theory.
The value of the Boltzmann constant is:
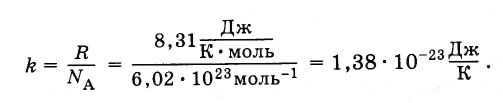
(4.5.4)
Considering the Boltzmann constant, equation (4.5.3) can be expressed in the following form:
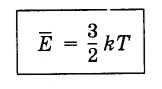
(4.5.5)
Significance of Boltzmann’s constant in physics
In the past, temperature was initially introduced as a thermodynamic measure, and a unit of measurement, the degree, was established for it (see section 3.2). Once the relationship between temperature and the average kinetic energy of molecules was established, it became evident that temperature could be defined as the average kinetic energy of molecules and expressed in joules or ergs. Instead of the value of T, the value T* can be introduced.
The temperature defined in this way is connected to the temperature expressed in degrees by the following relationship:
Therefore, Boltzmann’s constant can be seen as a quantity that links temperature expressed in energy units to temperature expressed in degrees.
By rearranging the equation (4.5.5) and plugging it into formula (4.4.10), we can derive an expression that illustrates how gas pressure depends on the concentration of molecules and temperature:
(4.5.6)
From formula (4.5.6), we can conclude that under the same pressures and temperatures, the concentration of molecules in all gases is identical.
This leads us to Avogadro’s law: gases of equal volumes at equal temperatures and pressures contain the same number of molecules.
The average kinetic energy of molecules’ translational motion is directly proportional to the absolute temperature. The constant of proportionality, known as the Boltzmann constant, k = 10 -23 J/K, must be memorized.
§ 4.6. Maxwell distribution
In many instances, simply knowing the average values of physical quantities is inadequate. For instance, having knowledge of the average height of individuals does not provide the ability to effectively plan the production of garments in various sizes. It is essential to ascertain the approximate number of individuals whose height falls within a specific range. Similarly, understanding the quantities of molecules that possess velocities different from the average value is crucial. Maxwell was the pioneer in discovering methods for determining these quantities.
In ยง4.1, we previously discussed how J. Maxwell first introduced the idea of probability to explain the actions of a vast collection of molecules.
As it has been stressed numerous times, it is fundamentally impossible to track the change in velocity (or momentum) of an individual molecule over an extended period of time. Moreover, accurately determining the velocities of all gas molecules at a specific moment in time is unattainable. The macroscopic conditions in which the gas exists (such as volume and temperature) do not necessarily dictate the velocities of the molecules. The velocity of a molecule can be considered a random variable, capable of assuming different values under given macroscopic conditions, similar to how a dice can yield any number of points from one to six (since a dice has six sides). It is impossible to predict the exact number of points that will be rolled on a dice, but it is possible to calculate the probability of, for example, rolling five points.
What is the likelihood of a random event occurring? Let’s consider a large number N of trials (N – number of dice throws). In this scenario, there were N‘ cases where the outcome was favorable (i.e. a five). Therefore, the probability of this event can be determined by dividing the number of favorable outcomes by the total number of trials, assuming the number of trials is sufficiently large:
(4.6.1)
When it comes to a dice with symmetrical sides, the likelihood of obtaining any specific number of points ranging from 1 to 6 is equal.
In the midst of a multitude of unpredictable events, we observe the emergence of a certain quantitative pattern, represented by a number. This number, known as probability, enables us to calculate average values. For example, if we were to roll a dice 300 times, the average number of times a five appears, as deduced from formula (4.6.1), would be: 300 divided by 50. It makes no difference whether we roll the same dice 300 times or roll 300 identical dice simultaneously, as the result remains the same.
The Boltzmann constant (
or 
) is a physical constant that establishes the correlation between temperature and energy. It is named after the Austrian physicist Ludwig Boltzmann, who made significant contributions to statistical physics, where this constant plays a crucial role. Its measured value in the International System of Units (SI) is: ![k=1<,></p>
[ZEBR_TAG_p><p>380\,648\,8(13)\times 10^” width=”” height=””> J/K [1].</p><p>The standard error for the value of the quantity is indicated in parentheses. The Boltzmann constant can be obtained by determining absolute temperature and other physical constants. However, calculating Boltzmann’s constant using basic principles is currently too complicated and impractical. [<i>source not stated for 257 days</i>] In Planck’s natural system of units, the natural unit of temperature is defined in such a way that the Boltzmann constant is equal to one.</p><p>The universal gas constant is defined as the product of the Boltzmann constant and the Avogadro number, . The gas constant is more convenient when the number of particles is given in moles.</p><h2>Relationship between temperature and energy</h2><p>In a uniform ideal gas at absolute temperature, the energy associated with each degree of freedom is equal to, according to Maxwell’s distribution, <img decoding=](https://dic.academic.ru/dic.nsf/ruwiki/33198e24a2c6c5179f17039ed261332c.png)
. At a temperature of 300 K, this energy is J, or 0.013 eV. In an ideal gas consisting of a single atom, each atom has three degrees of freedom corresponding to the three spatial axes, meaning that each atom has an energy of .
By having knowledge of the thermal energy, one can determine the root mean square (RMS) velocity of atoms, which is inversely related to the square root of their atomic mass. The RMS velocity of atoms at room temperature ranges from 1370 m/s for helium to 240 m/s for xenon. However, the situation becomes more complex when dealing with a molecular gas. For instance, a two-atom gas possesses roughly five degrees of freedom.
Entropy explanation
Entropy is a term used in various fields, including science and information theory, to describe the measure of disorder or randomness in a system. It quantifies the unpredictability or uncertainty associated with a set of data or the state of a system.
The definition of the entropy of a thermodynamic system can be expressed as the logarithm of the count of distinct microstates associated with a specific macroscopic state (for example, a state with a specific total energy).
The Boltzmann constant, denoted by , serves as the coefficient of proportionality in statistical mechanics. It establishes the relationship between the microscopic state variable () and the macroscopic state variable (
), encapsulating the fundamental concept of this branch of physics.
Additional Information
Important Details
The Boltzmann constant ( k or kb ) is a physical constant that establishes the correlation between temperature and energy. It is named after the distinguished Austrian physicist Ludwig Boltzmann, who made significant contributions to the field of statistical physics, in which this constant serves as a fundamental factor. In the SI system, its experimental value is equivalent to
J/K.
The values in parentheses represent the standard error in the last digits of the quantity’s value. In theory, the Boltzmann constant can be determined by measuring absolute temperature and other physical constants. However, the calculation of the Boltzmann constant based on fundamental principles is currently too complex and impractical. In Planck’s system of natural units, the unit of temperature is defined such that the Boltzmann constant is equal to one.
The universal gas constant is defined as the product of the Boltzmann constant and Avogadro’s number, R = kNA. The gas constant is more convenient when the quantity of particles is given in moles.
The correlation between temperature and energy is
The energy of a one-atom ideal gas is equal to 0.013 eV, or J. Each atom in the gas has three degrees of freedom, representing the three spatial axes. This means that each atom has an energy of 3/2(kT).
By knowing the thermal energy, we can determine the root mean square (RMS) velocity of the atoms. The RMS velocity is inversely proportional to the square root of the atomic mass. At room temperature, the RMS velocity ranges from 1370 m/s for helium to 240 m/s for xenon. However, in the case of a molecular gas, such as a two-atom gas, the situation becomes more complex as there are approximately five degrees of freedom.
The entropy of a thermodynamic system is the logarithm of the number of different microstates, denoted by Z, that correspond to a specific macroscopic state, such as a state with a particular total energy.
The Boltzmann constant, denoted by k, is the coefficient of proportionality in the expression that relates the microscopic states (Z) to the macroscopic states (S), and it represents the fundamental concept of statistical mechanics.
Related Articles
Wikimedia Foundation. 2010.
Boltzmann constant (k or kb) is a physical constant that establishes the connection between temperature and energy. It is named after Ludwig Boltzmann, an Austrian physicist who made significant contributions to statistical physics, where this constant plays a pivotal role. In the SI system, its experimental value is equal to
J/K.
The values in brackets represent the standard error in the last digits of the value. The Boltzmann constant can theoretically be determined from the measurement of absolute temperature and other physical constants. However, the calculation of the Boltzmann constant using fundamental principles is currently too complex and impractical. In Planck’s natural system of units, the natural unit of temperature is defined in such a way that the Boltzmann constant is equal to one.
The universal gas constant is defined as the product of the Boltzmann constant and Avogadro’s number, R = kNA. The gas constant is more convenient when the number of particles is given in moles.
The correlation between temperature and energy
Energy is a fundamental concept in physics, and its relationship with temperature is crucial to understand various phenomena. In a one-atom ideal gas, each atom possesses three degrees of freedom associated with the three spatial axes. Consequently, every atom has an energy of 3 / 2(kT) where k represents the Boltzmann constant and T denotes the temperature.
By knowing the thermal energy, we can determine the root mean square (RMS) velocity of the atoms, which is inversely proportional to the square root of the atomic mass. The RMS velocity at room temperature differs depending on the gas, ranging from 1370 m/s for helium to 240 m/s for xenon. In the case of a molecular gas, such as a two-atom gas, the situation becomes more intricate as it possesses approximately five degrees of freedom.
The entropy of a thermodynamic system is the logarithm of the number of different microstates Z corresponding to a given macroscopic state (e.g., a state with a specific total energy).
The Boltzmann constant k is a coefficient of proportionality. This equation, which establishes the connection between the microscopic ( Z ) and macroscopic states ( S ), represents the fundamental concept of statistical mechanics.
