While stars can vary in their physical characteristics, there are certain limitations to what is possible. Not every star that can be imagined by humans can actually exist. Stars are cosmic bodies that can only possess a certain amount of mass within certain limits.
If the mass of a celestial body is less than 0.02 times the mass of the sun, it cannot become self-luminous. As mass increases, the pressure and temperature inside the body reach levels where nuclear energy is released from the substance, similar to steam from boiling water. This implies that stars with masses equal to, for example, Earth or even Jupiter, cannot exist. These considerations establish a minimum limit for the possible masses of stars.
The “attributes” of stars were discussed earlier. The primary attributes of a star include mass, radius (excluding the outer transparent layers), and luminosity (the total amount of radiated energy); these values are often expressed as fractions of the mass, radius, and luminosity of the Sun. Along with the fundamental parameters, their derivatives are also utilized: effective temperature; spectral class, which indicates the level of ionization and excitation of atoms in the star’s atmosphere; absolute stellar magnitude (i.e., the stellar magnitude that a star would have at a standard distance of 10 parsecs). Let’s delve into some of these aspects in more depth.
The masses of stars
Indeed, the field of astronomy has not had and currently does not possess a means of directly and autonomously determining the mass of a solitary star, that is, one not part of a multiple system. This deficiency in our understanding of the Universe is quite significant. If such a technique were available, our understanding would advance much more rapidly. “The masses of stars generally fall within a relatively narrow range. There are only a small number of stars whose masses deviate by a factor of 10 or more from that of the Sun.”
When faced with this scenario, astronomers implicitly acknowledge that stars with matching luminosity and color possess identical masses. This conclusion is only reached in the case of double systems. However, it is important to exercise caution when assuming that a single star, which shares the same luminosity and color as its “sister” star in a double system, also possesses the same mass. This assertion can be derived from Newton’s generalization of the law of universal gravitation and Kepler’s laws, yielding the formula:
a3
M1 + M2 = —
3P2
To be more precise, the star’s observed wavy path is caused by the combination of two motions in which it is simultaneously involved – its movement around the center of the Galaxy and its orbit around the shared center of mass with its unseen companion.
This undetectable celestial object cannot be classified as a planet. With a mass of 0.024 times that of the sun, it surpasses the minimum mass required for an object to become a star. Consequently, it is certain that the 61 Swan system is composed of three stars, with the third component being an imperceptible star with one of the lowest masses. Nature also imposes limitations on stars with extremely large masses. To comprehend the reason behind this constraint, let’s attempt to envision the conditions within any star’s core.
Every normal star is a tremendously hot gas sphere. At every point of the star, there are three forces in action. First, the force of gravity attracts a particle of the star towards its center. Second, the gas pressure, in its attempt to expand, pushes the same particle in the opposite direction, towards the surface of the star. And finally, thirdly, the pressure of light, which emerges from the interior of the star and combines its forces with the gas pressure as it moves towards the outside. At each point of the star, the three forces engage in a constant struggle, resulting in a state of equilibrium. This equilibrium is what keeps the star stable. Any significant predominance of one force over the others would have catastrophic consequences for the star. For instance, if the pressure of light or gas were to suddenly and dramatically increase, the star would collapse.
If the star were to cease emitting light or if the gas were to suddenly lose its elasticity, the star would undergo a violent contraction and transition into a different, “non-stellar” state. In reality, the stars we observe are primarily characterized by their stability and equilibrium. However, this may not always hold true. As the mass of a star increases, so does its luminosity, which refers to the amount of light emitted from the star’s interior. At extremely large masses, such as thousands of times the mass of the Sun, the equilibrium between the three forces is inevitably disrupted. The pressure exerted by light would become so immense that it would destabilize the star from within.
The density of celestial bodies
Stellar brightness
Stars vary in their brightness, with some appearing brighter and others appearing fainter. However, this measurement alone does not provide an accurate indication of a star’s true radiative power, as distance plays a significant role. Therefore, apparent stellar magnitude cannot serve as a definitive characteristic of a star due to its dependence on distance. The true characteristic that we use is luminosity, which represents the total energy emitted by a star per unit time. The luminosities of stars exhibit a wide range of values. For example, the giant star S Goldfish has a luminosity that is 500,000 times greater than the luminosity of the Sun, while the faintest dwarf stars have a luminosity that is approximately the same number of times lower.
“The quality of brightness is known as the absolute magnitude of a star. The apparent magnitude of a star is influenced by its brightness and color, as well as its distance from us. When a star is brought to a standard distance of 10 parsecs, its magnitude is referred to as “absolute”. Let’s illustrate this with an example.”
If the Sun’s apparent magnitude (the brightness as seen from Earth) is -26.8, then when it is observed at a distance of 10 parsecs (which is approximately 2 million times the actual distance from the Earth to the Sun), its magnitude will be approximately +5. At this distance, our Sun, which is the source of daylight, would appear as a small star that is barely visible to the naked eye (keep in mind that the faintest stars visible to the naked eye have a magnitude of +6). Stars with high luminosity have negative absolute magnitudes, such as -7 or -5. On the other hand, stars with low luminosity have large positive absolute magnitudes, for example +10 or +12, and so on.
If you have the absolute stellar magnitude, you can determine the luminosity of any star by using the following formula: lg L = 0.4(M-Ms), where: L represents the luminosity of the star, M is the absolute stellar magnitude, and Ms is the absolute stellar magnitude of the Sun.”
Which star possesses the highest density?
Stars can be considered the most significant entities in the Universe, as they comprise over 90% of all the matter we observe.
Every star is a colossal mass of gas that emits its own light, in contrast to planets that shine through reflected sunlight. Stars share a common nature with the Sun, which happens to be the nearest star to Earth.
All stars are incredibly far away from us, with the distance to each one, excluding the Sun, being several times greater than the distance between Earth and any of the planets in our solar system. A direct method of determining the distances to relatively close stars is based on measuring their observable displacement against the backdrop of more distant stars, which is caused by Earth’s movement around the Sun.
The nearest star to our Solar System, Proxima Centauri, is approximately 1.3 parsecs away. Many stars that can be seen with the naked eye are situated tens or hundreds of light years distant.
Stars differ in their mass, size, density, luminosity, and chemical composition.
Let’s examine these characteristics in greater detail.
To determine the masses of stars, we observe the movements of stars in pairs and groups. In these binary and multiple star systems, stars exert gravitational attraction on each other, orbiting a common center of mass. The masses of stars are calculated using the law of universal gravitation. The mass of a star is often expressed in terms of solar masses, with one solar mass being equivalent to about 2-10^30 kg. The majority of stars have masses ranging from 0.1 to 50 times that of the Sun.
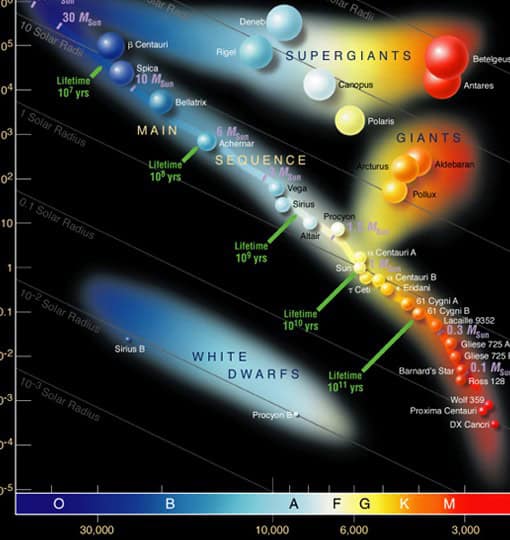
The sizes of stars are determined through various methods, including optical interferometers for direct measurements and theoretical calculations. It has been discovered that most observed stars have sizes ranging from hundreds of thousands to millions of kilometers. For instance, the Sun has a diameter of 1,392,000 kilometers. However, there are also extremely small stars, such as white dwarfs and neutron stars, which have diameters of only 10-20 kilometers. On the other hand, there are stars that are much larger than the Sun, known as giants (such as Betelgeuse, Arcturus, and Antares). Nevertheless, the largest stars are extremely rare and are known as red supergiants. If any of these stars were to replace the Sun, the orbit of Mars or even Jupiter would fit comfortably within their vast expanse!
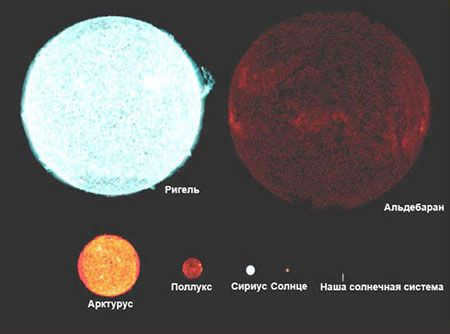
Comparison of star sizes
Stars vary greatly in size rather than mass. Consequently, smaller stars generally have a higher density of matter, while larger stars have a lower density. Giant stars and supergiants can have a lower density than air on Earth. The average density of solar matter is 1.4 times that of water. White dwarfs are significantly denser than the Sun. The substance of Sirius B, for example, has a mass of over 50 kg per 1 cm3. Some white dwarfs are even tens of times denser. However, neutron stars hold the density record, with a density equal to that of atomic nuclei – 10^14 g/cm^3. Such density can be achieved by compressing the entire globe to the size of half a kilometer!
Stars differ not only in size but also in their luminosity. Luminosity refers to the amount of optical radiation or light energy that a star emits per second. Typically, luminosity is measured in terms of the Sun’s luminosity, which is approximately 3.8-10 26 W. The majority of observed stars have luminosities ranging from a few thousandths to a million times that of the Sun.
The chemical composition of stars can be determined by analyzing their spectrum. Surprisingly, stars contain the same elements that are found on Earth. Hydrogen and helium make up more than 98% of a star’s mass, with hydrogen being about 2.7 times more abundant than helium. The remaining 2% of the mass consists of other elements.
Stars are not transparent, so we can only directly analyze the chemical composition of their outer layers, where the light we see originates from. However, through theoretical calculations, we are able to estimate the presence of different elements within the interior of stars.
Based on the physical properties of matter, stars can be classified into three main categories: normal stars, white dwarfs, and neutron stars.
Normal stars, which include the majority of observed stars, encompass those that are visible to the naked eye or through a small telescope. These stars are composed of a gas that possesses ordinary properties known as an ideal gas. The pressure of this gas is directly proportional to its temperature and inversely proportional to the volume it occupies. By applying the physical laws governing the behavior of this gas, astronomers are able to calculate the density, pressure, and temperature within the interior of stars. This information is crucial for comprehending the structure and evolution of stars.
In stars with extremely high densities, the matter no longer adheres to the laws governing ideal gas. Instead, it exhibits different properties and is referred to as degenerate gas. White dwarfs, as well as the cores of certain giant stars, are composed of degenerate gas.
The gravitational force affects the composition of every star, causing it to contract. However, stars do not rapidly decrease in size due to the counteracting pressure force exerted by the stellar matter. In typical stars, this pressure is a result of the elastic characteristics of the highly heated ideal gas. In white dwarfs, the degenerate gas pressure prevents compression and is not significantly influenced by temperature. In neutron stars, gravity is impeded by the nuclear forces that interact between individual neutrons.
The internal energy sources in stars maintain the temperature and thermal pressure of the gas. When these sources eventually run out, gravitational forces will compress the star into a dense ball. In normal stars, the highest density and temperature of the gas are found in the central region where energy is constantly produced. This energy is generated through thermonuclear reactions between hydrogen nuclei, converting hydrogen into helium. This process releases energy that allows stars to maintain high temperatures over time, but the reserves of hydrogen in stars gradually deplete. For example, in the Sun, the amount of hydrogen decreases by about 600 million tons every second, along with a similar decrease in helium. This results in the release of energy equivalent to approximately 3.8-10,26 J, which is carried away by electromagnetic waves. A small percentage of this energy is absorbed by neutrinos, elementary particles that are produced during nuclear reactions. These neutrinos easily pass through the star and travel at the speed of light into interstellar space.
Based on the current knowledge of science, the majority of elements beyond helium found in the natural world were created through thermonuclear reactions within stars or through reactions that take place during supernova explosions.
During the initial stages of a star’s life, when nuclear reactions have yet to occur, its energy can be sourced from the compression of stellar matter. This compression occurs as a result of the star’s own gravity, causing the potential energy of the matter to decrease and transform into thermal energy.
Stars, like all natural bodies, undergo a series of transformations throughout their existence. They are born, go through various stages of development, and ultimately reach the end of their lives.
The duration of a star’s life is determined by its mass. Stars that are smaller in mass than the Sun are incredibly efficient in their utilization of nuclear fuel, allowing them to emit light for billions of years. As a result, these low-mass stars have yet to experience the effects of aging. However, high-mass stars have a relatively short lifespan. For instance, stars with a mass of 15 times that of the Sun deplete their energy reserves in a mere 10 million years. In comparison, stars similar to our Sun can exist for approximately a thousand times longer.
Throughout most of its lifespan, a star maintains a relatively constant temperature and size. However, once all the hydrogen in the central region is depleted and converted into helium, the star undergoes rapid changes. It expands in size, and despite a decrease in surface temperature, the star emits significantly more energy. This transformation causes the star to become a red giant. The temperature in the central region skyrockets to 100 million degrees Celsius, and in the dense helium core of such a star, the helium-to-carbon reaction is “ignited”.
During a specific phase of the red giant’s evolution, the outer layers of this enlarged star may be shed, resulting in the star being surrounded by a gas ring known as a planetary nebula. The star itself will then contract and gradually cool down, eventually becoming a white dwarf.
Our Sun is on a trajectory of development that will lead it to become a white dwarf in about 6-7 billion years, after it goes through the red giant phase.
Stars with a mass 1.4 times greater than that of the Sun will not be able to halt their contraction at the white dwarf stage at the end of their life. The intense gravitational forces will compress them to a density where “neutronization” of matter occurs: the interaction between electrons and protons will result in almost all of the star’s mass being contained in neutrons. This leads to the formation of a neutron star. Neutron stars can be formed by the most massive stars after they undergo supernova explosions. Calculations indicate that neutron stars are likely to have strong magnetic fields. Their rapid rotation enables them to emit powerful streams of radio waves. The pulsating sources of radio emissions known as pulsars, discovered in the 1960s, are believed to be rotating neutron stars that formed after supernova explosions.
If a star’s mass (or the mass of its “remnant” after losing matter) is greater than 3-5 solar masses, then it will continue to contract even at the neutron star stage after reaching the end of its active life. This unrestrained gravitational contraction ultimately leads to the creation of a black hole.


There is no such thing as a perfect void in the Universe. Even in the vast expanse between galaxies, particles exist, along with peculiar entities like antimatter and dark energy. Hence, each region of the cosmos possesses a certain level of density.
From the water we consume to the core of a neutron star, every substance exhibits a density that spans from infinitesimally minute values (in the cosmic vacuum) to extraordinarily immense values that surpass our comprehension.
There are objects so densely packed that they highlight the astonishing (yet simultaneously unsettling) nature of the universe. And this is precisely what would cross your mind if we were to inform you that a tablespoon of a specific star would weigh as much as all the automobiles ever created by humanity. This entire weight amounts to the size of a tablespoon of sugar.
Today, our focus will be on exploring the vast expanse of the universe in search of materials and objects with the highest density. Prepare to be amazed as we uncover some truly remarkable discoveries.
So, what exactly is density?
Before we delve into the analysis of the densest objects in the Universe, it is crucial to have a clear understanding of what density entails. Density is a fundamental concept extensively utilized in the realms of physics and chemistry, which quantifies the relationship between an object’s mass and its volume.
Every material object, including everything we observe, possesses a specific density value that is determined by its weight per unit volume. To better grasp this concept, let’s consider an illustrative example.
Let’s say we have two rocks and we want to determine which one is more dense. To do this, we need to find their mass and volume. The first rock weighs 7000 kg and the second rock weighs 2000 kg. At first glance, we might assume (incorrectly) that the first rock is denser since it weighs more. However, that is not the case. Here we are not concerned with which rock weighs more on its own, but rather the one that weighs more per unit volume.
So, let’s consider their volumes. In this scenario, we find that the first rock has a volume of 1 cubic meter (which is the most commonly used unit for density calculations) and the second rock has a volume of 0.1 cubic meter.
When the mass and volume are known, the density can be determined by dividing the mass by the volume. Thus, the first object (weighing 7000 kg and having a volume of 1 m3) has a density of 7000 kg/m3, indicating that each cubic meter of rock weighs 7000 kg. If we had 2 cubic meters of this rock, it would have a weight of 14,000 kg.
On the other hand, the second object (with a mass of 2,000 kg and a volume of 0.1 m3) has a density of 20,000 kg/m3, indicating that each cubic meter of this second rock weighs 20,000 kg. Therefore, the second rock is denser, as if we were to compare the same volume (1 cubic meter) of both rocks, the second rock would be larger.
This concept of density applies to various materials and objects in the universe. By studying density, we can gain insights into the properties of different substances and deepen our understanding of the cosmos.
What are the most dense objects in the Cosmos?
Now that we understand the concept of density, which is defined as “the amount of weight an object has per unit volume”, let’s examine the densest bodies and objects in the Universe.
We will express their density in kilograms (kg) per cubic meter, which is a commonly used unit of measurement. It’s important to keep in mind that water has a density of 997 kilograms per cubic meter, as this will give us a reference point for the astronomical numbers we will encounter.
10. Iridium: 22,560 kg / m3.
The list kicks off with the most dense elements found on the periodic table. Iridium takes the third spot in terms of density in the entire universe, with a weight of 22,560 kg per cubic meter. This metal is even denser than the Earth’s core, as it possesses a density of 13,000 kg/m3. While this fact is truly remarkable, we have only scratched the surface of what’s to come.

9. Osmium: 22,570 kg/m3.
Continuing with osmium, the element with the greatest density in the entire universe.. And we naturally emphasize this fact. With a density of 22,570 kg/m3, osmium holds the record as the chemical element with the highest density. It is a metallic element that is utilized in certain alloys containing platinum.

8. Hassio: 40,700 kg / m3.
Potassium, which has a density of 40,700 kg/m3, holds the title of being the densest element in the universe. However, it is important to note that potassium is not a naturally occurring element. It is actually an artificial element that was first created by German scientists in 1984. These scientists were able to generate potassium atoms by fusing atoms of lead and iron together. While potassium’s density is impressive, its practical applications are limited. Its main significance lies in its status as the densest known element in the universe. It is worth mentioning that potassium has a very short half-life, which means that it decays rapidly. In fact, its half-life is less than 10 seconds.

7. The density of the core of the Sun is 150,000 kg/m3
When we consider the Sun as a reference, we can apply this information to most stars that are similar in density, whether they are lower or higher. As a general rule, the core of a star is where we find the highest density. In fact, the density of the Sun’s core is about four times greater than that of potassium. However, at this point, the core starts to resemble something out of a science fiction movie.
Although the density of the Sun’s core is incredibly high due to the immense pressure that exists within it, it is important to note that the Sun is primarily composed of hydrogen atoms, which are actually the least dense element in the universe. These atoms are compacted together to form plasma. Once we start observing stars composed of subatomic particles and studying the inner workings of black holes, our understanding of density will be completely transformed.

6. White dwarf: 10,000,000,000,000,000,000,000,000 kg/m3.
Picture the Sun decreasing in size until it is as small as the Earth. Its mass of 1'9 x 10 ^ 30 kg is comparable to that of a small planet. Here we have a white dwarf, a star that is 66,000 times denser than a star like the Sun. White dwarfs are not simply a type of star, but rather the final phase in the lifecycle of certain stars. As they approach their demise, these stars begin to collapse due to the gravitational force of their own core, resulting in an incredibly condensed state.

5. Neutron star: 10 ^ 17 kg/m3.
Prepare to be amazed if you were surprised by a white dwarf. Because in the vast expanse of the universe, there exists a star that is 8 billion times denser than the aforementioned white dwarf. To put this into perspective, let’s imagine that we were able to shrink the Sun down to the size of Manhattan Island. This would give rise to a neutron star. In reality, a neutron star has a diameter of only 10 kilometers and a mass twice that of the Sun. It truly is a mind-boggling phenomenon.
Neutron stars are among the most mysterious entities in the realm of astronomy, and currently, they are the densest celestial objects in the known Universe. These extraordinary stars are born from the cataclysmic explosion of a supermassive star (millions of times larger than our Sun), leaving behind a compact core where the protons and electrons of their constituent atoms merge, eliminating any repulsive forces between them and allowing for the attainment of these mind-boggling densities.

4. Quark Plasma: 10 ^ 19 kg / m3.
We continue to explore the extraordinary phenomena, some of which have yet to be observed naturally. Let’s begin this new phase with the quark plasma, believed to have existed in the early moments of the Universe, just a few milliseconds after the Big Bang.
This incredibly dense plasma contained all the elements that would eventually form the cosmos. Its existence was confirmed in 2011, when scientists at The Large Hadron Collider successfully created this matter by colliding lead atoms (apologies for the redundancy) at nearly the speed of light.

3. Preon star: 10 ^ 23 kg/m3
Among the most dense objects in the Universe, there are some whose existence has not been proven and is only based on theoretical assumptions in the field of physics. Therefore, currently, the densest known matter in the Universe is the quark plasma mentioned above.
Preon stars, which could theoretically exist according to the laws of physics, are incredibly small and therefore undetectable. Scientists in the field of astrophysics propose that certain subatomic particles, such as quarks, could come together to form these unique stars. The density of a preon star would be a staggering 47 million times greater than that of a neutron star. To put it into perspective, imagine if the entire mass of the Sun were compressed into a golf ball – that’s the size of a preon star. However, it’s important to note that the existence of preon stars has yet to be proven and currently remains purely hypothetical.

2. Planck particle: 10 ^ 96 kg / m3.
Adding to the strangeness, we have now reached the realm of Planck density. The Planck particle is a theoretical subatomic particle that is characterized as a minuscule black hole. It is incredibly tiny and incredibly heavy, with a weight that is 13 million quadrillion times greater than that of a proton, while being trillions of times smaller in size.
This concept is beyond our comprehension. By definition, a black hole is a point in space with such an immense density that it generates a gravitational force so strong that even light cannot escape. Hence, we refer to the Planck particle as a “miniature black hole.”
1. Black hole: the highest density
We ended in a magnificent way. A black hole is the most compact object in the universe. And nothing will ever dethrone it because the laws of physics prohibit any further increase in density. A black hole represents a singularity in space, which means it is a point with infinite mass and zero volume. Consequently, according to mathematical calculations, its density is infinite. This immense density generates an enormous gravitational force, so powerful that even light cannot escape its gravitational pull. However, beyond this point, we can only speculate about what occurs inside a black hole. It will forever remain a mystery.

At present, there are extra combined reductions (ranging from 2% to 25%) accessible to 58,744 educational establishments. To ascertain which reduction is applicable to all staff members of your educational establishment, please log in to your personal Infoworks account.


Enroll in our professional retraining course
Learn the pedagogy of additional education (arts and crafts)
We can apply a discount from your educational institution to this course (the amount depends on the number of your colleagues who have already taken Infoworks courses)
Currently, 58,744 educational institutions are eligible for additional discounts (ranging from 2% to 25%). To find out the specific discount available to all employees of your educational institution, please log in to your personal Infoworks account.


Course for professional development
Creating an inclusive environment for individuals with disabilities in educational institutions.
We can apply a discount to your educational institution in addition to this discount (the amount depends on the number of your colleagues who have completed Infowork courses).
Currently, there are additional cumulative discounts available for 58,744 educational institutions, ranging from 2% to 25%. To determine the discount applicable to all employees of your institution, please log in to your personal Infoworks account.




Homeschooling: Tips and Tricks for Parents
A Breakdown of the Presentation by Slide:

Typically, when determining the sizes of stars, one must rely on calculations derived from their luminosity and temperature.
The luminosity of a star can be calculated using the same formula applied to the Sun’s luminosity.


Slide 3: Stars that possess a very high luminosity are known as supergiants. They are called red supergiants due to their large size. Betelgeuse and Antares have diameters hundreds of times larger than that of the Sun. VV Cepheus, which is located further away, is so massive that it could accommodate a solar system with planets orbiting up to and including Jupiter’s orbit. However, despite their size, the masses of supergiants are only 30-40 times greater than that of the Sun. Consequently, the average density of supergiants is thousands of times lower than the density of air found in a room.

When comparing stars with the same luminosity, their size tends to be smaller as they get hotter. Red dwarfs, which are the smallest type of ordinary stars, have masses and radii that are a fraction of the size of the Sun. Additionally, their average densities are 10-100 times higher than water.
One example of a star with a known distance and orbit is Sirius, which is bright and located near us. Sirius has a companion star that orbits around it every 50 years. Both stars are white and have similar levels of heat. Despite this, the companion star is 10,000 times less bright in terms of luminosity compared to Sirius. As a result, its radius is 100 times smaller, making it similar in size to Earth. However, the companion star has a mass that is almost the same as the Sun. This means that the white dwarf has an extremely high density of approximately 109 kg/m3.

 5 slide The existence of a gas of such density has been explained in this way : normally, the density limit is set by the size of atoms, which are systems consisting of a nucleus and an electron shell. At very high temperature in the interior of stars and when atoms are fully ionized, their nuclei and electrons become independent of each other. At colossal pressure of overlying layers this “crumb” of particles can be compressed much more strongly than neutral gas. theoretically, the possibility of existence under some conditions of stars with density equal to the density of atomic nuclei is allowed.
5 slide The existence of a gas of such density has been explained in this way : normally, the density limit is set by the size of atoms, which are systems consisting of a nucleus and an electron shell. At very high temperature in the interior of stars and when atoms are fully ionized, their nuclei and electrons become independent of each other. At colossal pressure of overlying layers this “crumb” of particles can be compressed much more strongly than neutral gas. theoretically, the possibility of existence under some conditions of stars with density equal to the density of atomic nuclei is allowed.
What is the composition of matter inside neutron stars? Is it a neutron superfluid or strange quarks?
Neutron stars are known for their incredibly high density, which makes them one of the densest objects in the universe. However, the exact form of matter that exists inside these stars is still a subject of debate. Some theories suggest that the matter inside neutron stars could be in the form of a neutron superfluid, while others propose the presence of strange quarks. The extreme conditions inside neutron stars make it difficult to study them directly, so scientists rely on theoretical models and indirect observations to gain insights into their composition. Further research and observations are needed to unravel the mysteries of these enigmatic celestial objects.

When a star with a mass twenty times greater than that of the Sun reaches the end of its life, it transforms into a neutron star, a celestial body that has the dimensions of a large city and possesses an extraordinary density. According to astrophysicist Zaven Arzoumanian from NASA’s Goddard Space Flight Center, this is one of the most mind-boggling objects known to mankind. To put it into perspective, a piece of a neutron star the size of a ping-pong ball would have a weight exceeding one billion tons. Deep within the star’s core, which is subjected to immense gravitational pressure, the majority of protons and electrons would have combined to form neutrons, thus giving these stars their name. However, the true nature of these objects remains a topic of ongoing research and debate among astrophysicists.
The density within a neutron star is equivalent to that of an atomic nucleus, approximately 10 17 kilograms per cubic meter – a density that some laboratory experiments are just starting to replicate. In these extreme conditions, the internal composition of these objects remains largely mysterious. “These objects possess the highest stable matter density permitted by the laws of nature, yet in a manner that is not yet comprehended,” Zaven Arzoumanian explains. It is also a type of matter that encounters the most intense gravity: if you were to add a slight amount of additional mass, a neutron star would transform into a black hole that warps the surrounding space-time so profoundly that even light cannot escape it.
There are several theories regarding the internal structure of neutron stars. Some propose that the centers of neutron stars are simply filled with a dense phase of nucleons (the building blocks of atomic nuclei), with the majority being neutrons and a few protons scattered throughout. Other hypotheses involve more unusual configurations. One possibility is a combination of nucleons and hyperons, which are less common particles. Hyperons were discovered in the 1950s through particle accelerator experiments and related studies. Nucleons and hyperons are both types of composite particles known as baryons, each composed of three quarks: the proton contains two u quarks and one d quark, the neutron contains two d quarks and one u quark, while the hyperon consists of at least one s quark, which is a heavier and less stable version of the d quark. The core of a neutron star may also contain mesons, which are particles comprised of a quark and an antiquark. However, in an even more exotic scenario, neutrons could completely dissolve, releasing quarks and gluons (the particles that mediate the strong nuclear force and interact with quarks), resulting in a sea-like “plasma” of freely moving particles.
We are also receiving new information from the Nicer (Neutron star interior composition explorer) experiment, which was launched in June 2017 on the ISS. The main objective of this experiment is to observe pulsars, which are rapidly rotating neutron stars that possess a powerful magnetic field and emit light beams that serve as “beacons of the universe.” When these beams sweep across the Earth, we are able to witness pulsars flashing up to 700 times per second.
Thanks to these groundbreaking experiments, we now have a glimmer of hope in regards to expanding our knowledge on the internal structure of neutron stars, as well as gaining a deeper understanding of how matter behaves under the most extreme conditions imaginable.
Explosive birth
Neutron stars come into existence during extreme cosmic events called supernovae. When a giant star exhausts its nuclear fuel, it is no longer able to withstand its own gravitational force, leading to a collapse. This collapse results in a rapid expulsion of the star’s outer layers into space, while its core, mainly consisting of iron at this stage, undergoes compression.
The force of gravity is so strong that it effectively crushes the atoms, causing the electrons to be pushed into the core where they merge with protons to create neutrons. According to Mark Alford, a physicist at Washington University in St. Louis, this compression of iron is happening in all directions and results in it being compressed 100,000 times. In fact, an atom that is a tenth of a nanometer in size is transformed into a beam of neutrons that is several femtometers in diameter. (For reference, a femtometer is one millionth of a nanometer, which in turn is one billionth of a meter.) This compression is so intense that it is as if the entire Earth were reduced to the size of a city block. By the end of this collapse, the remaining matter in the star consists of approximately 20 neutrons for every proton.

According to James Lattimer, an astronomer at Stony Brook University, a neutron star can be compared to a single enormous atomic nucleus, but with one significant distinction: while nuclear interactions create cohesion within a nucleus, gravity serves as the cohesive force in a neutron star.
It is now believed that a neutron star contains no more than 10% hyperons.
In 1934, Walter Baade from Germany and Fritz Zwicky from Switzerland and the United States were the first to propose the idea that a supernova could lead to the formation of a neutron star. This concept was met with skepticism, as it had only been two years since British physicist James Chadwick discovered the neutron, and many scientists were unsure about the existence of such an extreme object. It wasn’t until 1967 when Jocelyn Bell Burnell, a doctoral candidate at the University of Cambridge in the UK, and her colleagues observed pulsars that the idea started to gain credibility. In the following year, the researchers determined that these pulsars must be rotating neutron stars.
According to astrophysicists who study them, neutron stars have masses ranging from 1 to 2.5 times that of the Sun. Neutron stars consist of at least three distinct layers. The outermost layer is a gaseous “atmosphere” made up of hydrogen and helium, measuring only a few centimeters in thickness. This atmospheric layer resides above an outer “crust” that is approximately one kilometer thick. The crust is composed of atomic iron nuclei arranged in a crystalline structure, with neutrons and electrons filling the spaces in between.
The remaining part of the star, the deeper region, is the subject of further speculation. As one approaches the core, the pressure intensifies, causing an increase in the number of neutrons within each atomic nucleus. However, there comes a point where the nuclei become saturated with neutrons, resulting in an overflow of neutrons and protons. At this juncture, the nuclei cease to exist and instead transform into a liquid state consisting solely of neutrons and protons. It is even possible that deep within the star’s core, these particles may eventually decay.
How does this liquid appear? It is conceivable that this substance takes on the form of a “superfluid,” a fluid devoid of viscosity that, according to theory, continues to move perpetually once set in motion. This peculiar state of matter is made possible by the attraction between quarks, which, when brought into close proximity, would form “Cooper pairs” similar to the behavior of electrons in superconducting substances.
A quark is a type of fermion particle with a spin value of 1/2 or 3/2, which is considered a half-integer value in the appropriate units. When two quarks are combined, they behave like a boson particle with an integer spin value such as 0 or 1. However, fermions and bosons follow different rules. Fermions adhere to the Pauli exclusion principle, which states that two identical fermions cannot occupy the same quantum state. This principle does not apply to bosons. In the case of a neutron star, individual quarks are forced to occupy higher energy states in order to satisfy the Pauli exclusion principle and the high density. However, when paired with bosons, quarks can remain in a lower energy state, which is the preferred configuration for any physical system. This allows the quark pairs to accumulate and form a superfluid state.
The extraordinary superfluid nucleus of neutron stars
Even in the periphery, within the external core, where neutrons remain undamaged, they also have the ability to establish a superfluid state. In reality, researchers possess a strong belief in the fact that neutrons exhibit this unique behavior. This conviction is derived from the careful observation of pulsar “glitches,” which are instances when the spinning motion of a neutron star experiences an abrupt acceleration.
According to experts, these errors happen when the overall rotation speed of the star stops matching the rotation of the superfluid underneath the surface. Typically, a star’s rotation slows down over time due to the release of energy through electromagnetic radiation and stellar wind. However, a frictionless superfluid does not experience this slowdown. The difference in velocity between the two layers creates mechanical stress, storing energy that is eventually released as angular momentum, causing the star to accelerate once again.
In 2011, James Lattimer and his colleagues claimed to have discovered indications of superfluidity within the central region of a neutron star. However, the scientific community remains divided on this matter. The research team, headed by Dany Page from the National Autonomous University of Mexico, examined fifteen years’ worth of X-ray data from Cassiopeia A, a supernova remnant that first appeared in the early 17th century. The astronomers observed that the pulsar located at the core of the nebula is cooling at a faster rate than predicted by current theories.
Neutron stars have the ability to possess superfluid in both their outer and inner core. In addition, they can also harbor a substance known as “strange matter,” which consists of quarks, specifically strange quarks (abbreviated as “s” in English).
What is “strange” matter?
There are six types of quarks: u, d, c, s, t, and b. Only the two lightest, U and D, can be found in atoms. The other quark species are heavier and less stable. They can be observed, for instance, in high-energy particle collisions at facilities like the LHC (Large Hadron Collider) at CERN, which is located near Geneva. However, they can also exist in the extremely dense core of neutron stars. In some cases, the u and d quarks that make up neutrons can transform into s quarks (it is unlikely that the other quarks would form under these extreme conditions due to their high mass). If s quarks appear and remain bound to other quarks, this could result in the creation of hyperons.
Lastly, it is conceivable that these quarks may exist within a quark-gluon plasma. Conducting experiments on particle accelerators could provide us with additional insights into the specific requirements for the emergence of hyperons, for instance. The Alice experiment, conducted at the LHC, is focused on investigating this particular form of matter. However, it is important to note that this synthetic plasma is generated under high temperatures and extremely low densities, which differ significantly from the conditions found within the core of a neutron star. The temperature within a neutron star is relatively cool, while the density is considerably higher.
One way to determine the composition of a neutron star’s core is by observing how the internal structure of the star affects its size. If the core contains intact neutrons, they will behave “like spheres and create a solid and compact core,” explains Zaven Arzoumanian. A compact core causes the outer layers to repel and increases the overall size of the star. On the other hand, if the neutrons were to dissolve into a mixture of quarks and gluons, the star would be smaller and “softer.” The Nicer experiment is investigating this phenomenon. “One of the main objectives is to measure the mass and radius of a neutron star,” says Zaven Arzoumanian, co-director and scientific director of the Nicer experiment. This research will also help to eliminate certain theories.”

The experiment Nicer is designed as a large container resembling a washing machine, positioned outside the International Space Station. Its purpose is to scan a multitude of pulsars dispersed throughout the sky and identify X-photons emitted by them. Through the measurement of these photons’ arrival time, energy, and the distortion caused by the powerful gravitational field of the stars, scientists will be able to determine the pulsars’ mass and radius, facilitating a comparison between them. According to Alford, if Nicer discovers stars with similar masses but significantly different radii, it would indicate the presence of unusual phenomena. This could potentially be attributed to a phase transition between two forms of matter, resulting in the contraction of the star. Such a transition might occur when neutrons decay into quarks and gluons.
Measuring the dimensions of neutron stars serves the purpose of narrowing down the potential manifestations of matter. For a considerable period of time, it was believed that half of the neutrons within a neutron star transformed into hyperons. Theoretical calculations indicated that the mass of a neutron star could not surpass 1.5 times that of the Sun. However, in 2010, Paul Demorest and his team from the U.S. Radio Astronomy Observatory in Virginia discovered a neutron star with a mass equivalent to 1.97 times that of the Sun, thus contradicting the initial prediction. Presently, physicists estimate that hyperons constitute no more than 10% of the overall composition of a neutron star.
Neutron stars can reveal even more intriguing information through fresh and distinct observations. Gamma-ray bursts, which have been captured by telescopes for many years, are believed to be the outcome of collisions between two neutron stars. This hypothesis was confirmed on August 17, 2017, when two instruments, Ligo (the Laser Interferometer Gravitational Wave Observatory located in Washington State and Louisiana) and Virgo (near Pisa, Italy), simultaneously detected gravitational waves emitted by a duo of neutron stars that orbit each other before ultimately colliding and merging.
Gravitational Wave Data: A Window into the Universe
In the past, the detection of gravitational waves, starting with the groundbreaking 2015 discovery, has primarily been attributed to the merging of two black holes. However, unlike the fusion of neutron stars, this phenomenon does not emit electromagnetic radiation. On August 17, 2017, a unique event occurred that provided valuable insights into the collision of these celestial bodies. The detection of both gravitational waves and electromagnetic radiation by numerous telescopes has revolutionized our understanding of neutron star physics. "It was an overwhelming experience"," admits James Lattimer. "I couldn’t believe my luck."
An examination of the signals revealed that the occurrence was the consequence of the clash between a duo of neutron stars positioned roughly 130 million light-years away from the planet Earth, each having a mass equivalent to 1.4 times that of the Sun and a diameter ranging from 11 to 15 kilometers prior to the collision. By utilizing this information, the scientists have enhanced the restrictions on the equation of state for neutron stars. This equation, which should be applicable to all neutron stars within the cosmos, elucidates the density of material as a function of pressure and temperature within the celestial body. Theorists have put forth various formulations corresponding to different conjectures regarding the composition of the substance contained within these celestial bodies, and the latest measurements have enabled them to dismiss some of said conjectures.
Up until now, Ligo and Virgo have only picked up on this one neutron star collision, but there is the potential for another similar event to happen at any given time, as both detection facilities have recently restarted their observation campaign.
Promising signs within the grasp of future detectors
Physicists are looking to further test their models as gravitational wave detectors become more sensitive. One way to do this is by studying the gravitational waves emitted by a possible rotating fluid inside a neutron star. If the fluid has very low viscosity or is a superfluid with zero viscosity, it will flow in certain patterns known as “r-modes,” which generate gravitational waves. According to Alford, these gravitational waves would be much weaker than those produced in a collision. Instead of being torn apart, the matter would quietly lap. Currently, the version of Advanced Ligo in use is not capable of detecting r-mode waves. However, future improvements to Ligo and planned observatories like the Einstein Telescope in Europe may have the capability to detect them.
What about the force of gravity?
Exploring the composition of neutron stars would provide us with a comprehensive understanding of the various forms that matter can assume, ranging from the commonplace to the extraordinary. Moreover, delving into the nature of neutron stars would yield additional advantages: not only would it enable us to examine nuclear interactions, but it would also offer a unique opportunity to gain insights into the enigmatic force of gravity.