The way in which all the planets in the solar system are affected by the gravitational force of the Sun is similar to the way the Moon and the Earth’s man-made satellites revolve around the Earth. This type of motion is referred to as central motion. Kepler’s laws govern this type of motion.

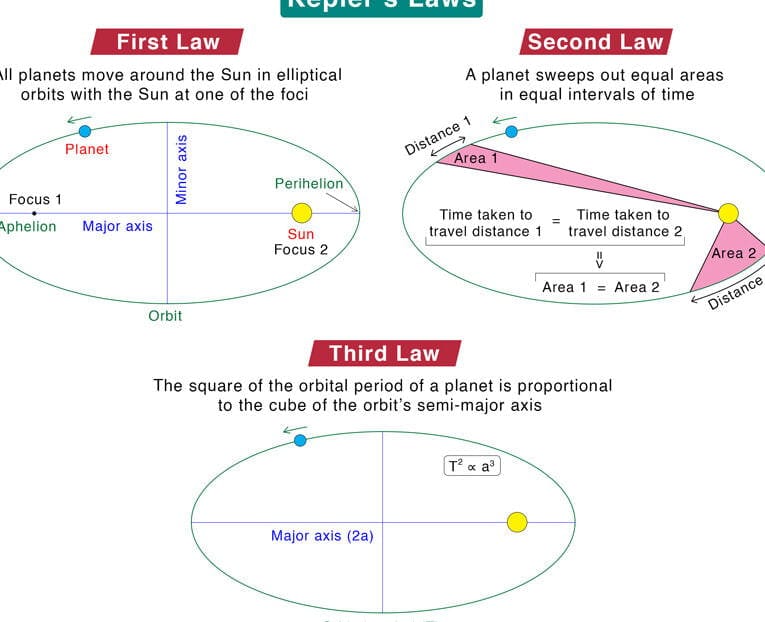
Kepler’s first law
The planets follow curved paths called ellipses, with one of the foci being occupied by the Sun.
Technically, both the Sun and the planets orbit a shared center of mass. However, this center of mass is located within the Sun, as the Sun has a significantly larger mass compared to the planets.
Kepler’s Second Law
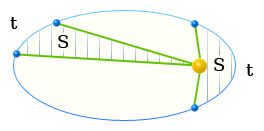
In equal periods of time, a planet sweeps out equal areas as it moves along its orbit, with a line joining the Sun and the planet.
The derivation of Kepler’s second law is based on the principle of conservation of angular momentum.
Kepler’s Third Law
The ratio of the cube of the average distance r to the square of the orbital period T is constant for all planetary orbits.
Kepler’s third law can be deduced from the requirement that the centripetal force acting on a planet must be equal to the gravitational force of attraction between the Sun and the planet.
| radius of the trajectory, | measured in meters |
| angular speed, | measured in radians per second |
| gravitational constant, | measured in cubic meters per kilogram per second squared |
| mass of the planet, | measured in kilograms |
| mass of the Sun, | measured in kilograms |
| orbital period, | measured in seconds |

Kepler’s First Law states that every planet revolves around the Sun in an elliptical orbit.


Every planet revolves around the Sun in an elliptical path with the Sun at one of its foci.
e = OS OA OO SS OS OA OOA OOS OA – eccentricity
O – center of the ellipse
Point A – perihelion
Point B – aphelion
OA = OB – major semi-axis
SA – perihelion distance
SB – aphelion distance
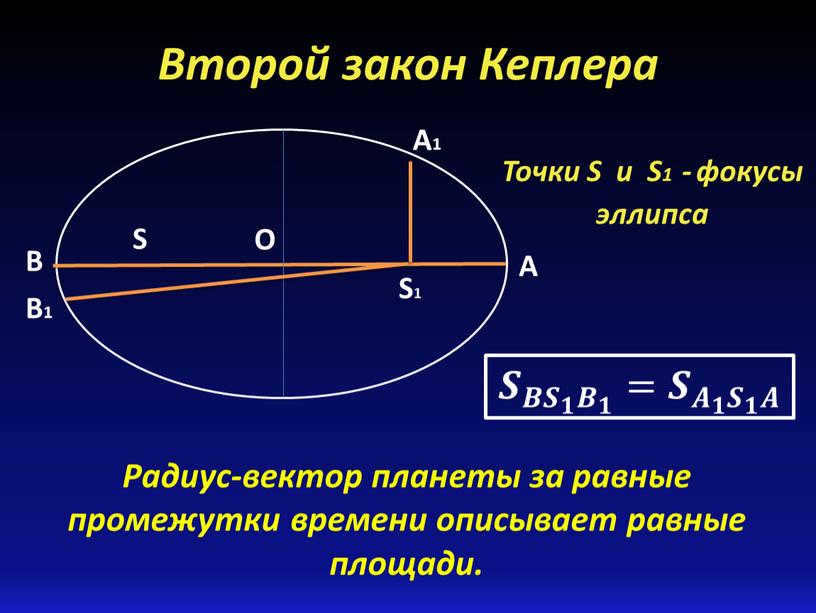
The planet’s radius vector traces out equal areas in equal time periods.
Points S and S1 represent the foci of the ellipse.
Kepler’s Third Law states that the squares of the orbital periods of the planets are proportional to the cubes of the major semi-axes of their orbits, denoted as 𝑻 1 2 𝑻 2 2 2 𝑻 1…
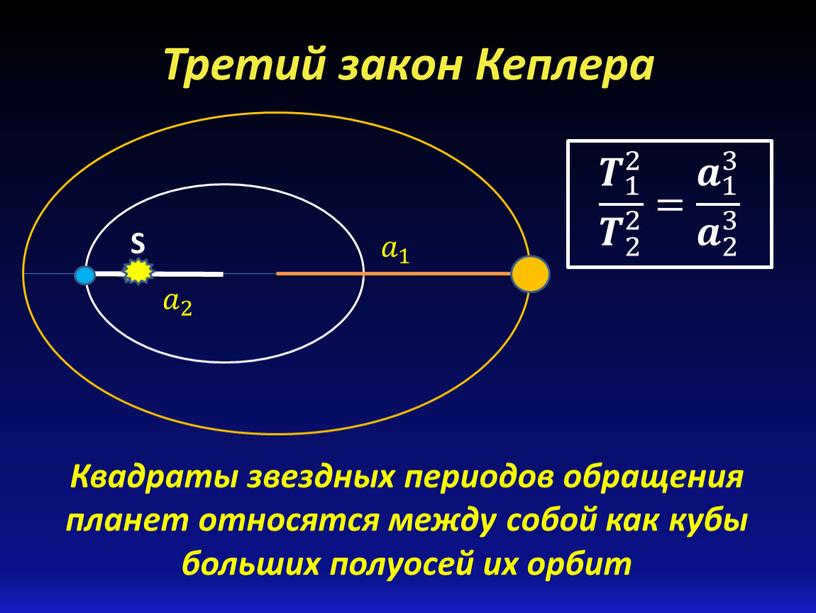
The relationship between the squares of the stellar periods of planetary orbits and the cubes of the major semi-axes of their orbits can be expressed as follows:
�� 1 2 �� 2 2 �� 1 2 ���� �� 1 2 1 �� 1 2 2 �� 1 2 �� 1 2 �� 2 2 �� 2 2 ���� �� 2 2 2 �� 2 2 2 �� 2 2 �� 1 2 �� 2 2 = �� 1 3 �� 2 3 �� 1 3 ���� �� 1 3 1 �� 1 3 3 �� 1 3 �� 1 3 �� 2 3 �� 2 3 ���� �� 2 3 2 �� 2 3 3 �� 2 3 �� 1 3 �� 2 3
The practical use of acquired knowledge
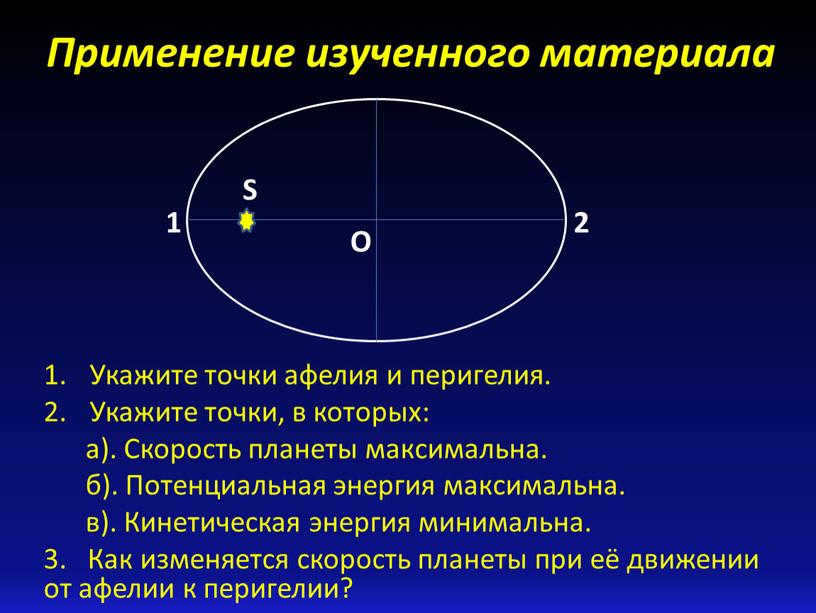
Utilization of the acquired knowledge
Identify the locations of aphelion and perihelion.
Specify the locations where:
a). The speed of the planet is at its maximum.
b). The potential energy is at its maximum.
c). Kinetic energy is at its minimum.
3. How does the speed of a planet change as it transitions from aphelion to perihelion?
Practical Application of Acquired Knowledge

Application of the material studied
Determine the orbital period of asteroid Belorussia, given that the major semi-axis of its orbit is a=2.40 a.u.
The orbital period of Jupiter around the Sun is T=12 years. What is the average distance from Jupiter to the Sun?
The average distance from the Earth to the Sun is equal to 1 astronomical unit (a.u.), which is equivalent to 150 million kilometers.
Generalizing and Systematizing the Boundaries of Law Applicability

Generalization and systematization
The boundaries of applicability of Kepler’s laws:
- Kepler’s laws are applicable for describing the motion of the planets, but they do not provide an explanation for the causes of motion.
- These laws allow us to calculate the relative distances of the planets from the Sun.
- Kepler’s laws are also applicable to the motion of the planets, their natural and artificial satellites, as well as the motion of other celestial bodies such as asteroids, comets, and stars in double systems.

– The heliocentric system of world order proposed by Copernicus was confirmed.
– Empirical data was used to overcome speculative conclusions about the circular motion of celestial bodies.
– The concept of the astronomical unit was introduced as a basis for calculating various astronomical distances in the solar system.
– These discoveries served as the foundation for the Titius-Bode law and the discovery of other laws.
Task §12, Exercise 10 (1, 2), complete the table:

§12, Exercise 10 (1, 2), fill out the chart:
References utilized: 1. Cone model

1. Model of a Cone in the Kepler System
Source (www.ck12.org)
2. Astronomy Manual for 11th Grade by M.A. Kunash
M. A. Kunash. – Moscow : Drofa, 2018. – 217, [7] p.
The information on this page is sourced from open ichonchiki or submitted by users in accordance with the site’s terms and conditions. Please report any violations.

There are currently extra cumulative discounts (ranging from 2% to 25%) available for 58,742 educational establishments. To determine which discount is applicable to all staff members of your educational institution, please access your personal Infoworks account.


Enroll in our professional retraining course today!
Occupational Safety
We are pleased to offer an exclusive discount to your educational institution. The amount of the discount will be determined based on the number of your colleagues who have already completed Infowork courses.
Currently, we are offering additional cumulative discounts ranging from 2% to 25% to a total of 58,742 educational institutions. To find out the specific discount available to all employees of your institution, simply log in to your personal Infoworks account.



Professional development course
Utilizing creative thinking techniques to foster general competences as per FSES.
We can combine your educational institution’s discount with this promotion (the amount will be determined based on the number of your colleagues who have completed Infowrok courses).
Currently, there are additional cumulative discounts (ranging from 2% to 25%) available for 58,742 educational institutions. To discover the applicable discount for all staff members of your educational institution, please log in to your personal Infoworks account.


Effective Time Management
Outline of the presentation by separate slides:

Slide 1: Summarizing and Explaining Newton and Kepler’s Laws
Presented by Irina Valerievna Kutuzova, Physics Teacher at VKK MBOE SOSH No. 54, Voronezh City.


On the second slide, Kepler empirically discovered his laws, while it took Newton almost four decades after Kepler’s death in 1666 to formulate the law of universal gravitation.


Slide 3: The Law of Universal Gravitation
All masses are drawn towards one another by a force, the magnitude of which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

Gravity is a fundamental characteristic of all objects in the natural world and has a significant impact on celestial bodies. Kepler’s laws provide insight into the paths that planets follow, while the law of universal gravitation explains the force that keeps celestial bodies in close proximity to each other. Additionally, gravity plays a crucial role in the formation and evolution of celestial bodies.

The area of astronomy that investigates the movement of celestial objects as a result of their gravitational pull on each other is known as celestial mechanics.


Slide 6: A planet’s orbit can become strictly elliptical due to the gravitational force exerted by a single body. However, other factors such as attraction from other planets and satellites can also affect a planet’s trajectory, causing deviations from a strictly elliptical shape. These deviations are known as perturbations.


7 slide Based on the deviations in the orbit of Uranus, John Adams and Urbain Leverrier calculated the exact position in space of an unidentified celestial body at that time, and on September 23, 1846, Johann Galle identified the eighth planet, Neptune.


Slide number 9: The First Law
When influenced by the force of gravity, a celestial body has the ability to move in relation to another celestial body in various shapes such as a circle, ellipse, parabola, or hyperbola. The specific shape of the orbit is determined by both the magnitude and direction of the initial velocity.
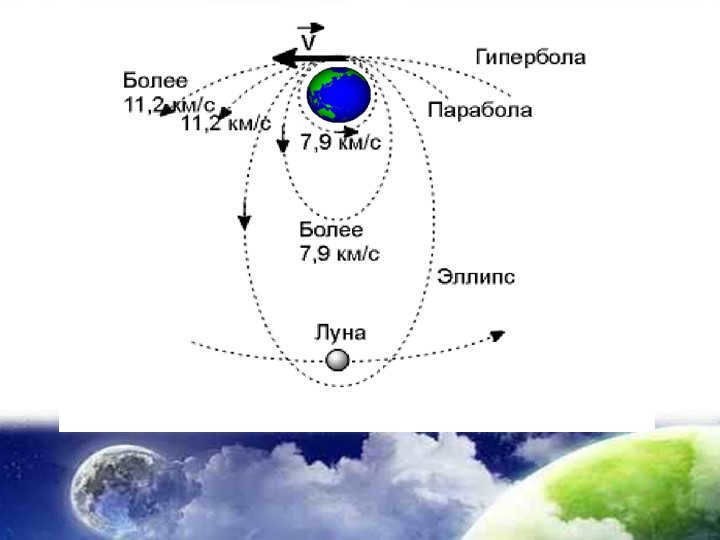
Slide 11: The Second Law
The planet’s radius vector remains constant as it describes equal areas at equal intervals of time.

The third law states that for two planets orbiting the Sun, the squares of their sideric periods multiplied by the sum of the masses of the Sun and the planet are proportional to the cubes of the major semi-axes of their orbits.

The third law, also known as the 12-slide Third Law, applies to the motion of two planets around the Sun. It states that the squares of the sideric periods of the two planets multiplied by the sum of the masses of the Sun and the planet are related to the cubes of the major semi-axes of the orbits of the planets.

Slide 13: The third law can be used to analyze the orbit of a planet and its satellite around the Sun.
Let’s define the following variables: m and T represent the mass and period of the planet, while m1 and T1 represent the mass and period of the satellite.


When considering the mass of celestial bodies, it is important to note that the Sun’s mass is many times greater than that of any planet. Additionally, a planet’s mass is usually much larger in comparison to the mass of a satellite. This fact allows us to accurately determine the ratio between the Sun’s mass and the mass of a planet:

Summary of the Document:
When a single body is in motion, it follows a strictly elliptical path. However, the presence of other planets, satellites, and other gravitational forces causes deviations from this elliptical trajectory. Newton expanded on Kepler’s laws by formulating the law of universal gravitation.


Currently, there are additional cumulative discounts (ranging from 2% to 25%) available to 58,742 educational institutions. To determine the discount applicable to all staff members of your educational institution, please sign in to your personal Infoworks account.


Professional training program
Work safety
We have the option to combine your educational institution’s discount with this discount (the amount depends on the number of your colleagues who have completed Infowork courses).
Currently, 58,742 educational institutions are eligible for additional discounts (ranging from 2% to 25%). To determine the discount applicable to all employees of your educational institution, please log in to your personal Infoworks account.




Advanced training program
Utilizing innovative thinking techniques to foster overall skills based on FSES
We can include your school’s discount along with this promotion (the amount depends on the number of your colleagues who have completed Infoworks courses)
Currently, 58,742 educational institutions are eligible for additional discounts (ranging from 2% to 25%). To determine the applicable discount for all staff members at your school, please login to your personal Infoworks account.


Efficient Use of Time
Breakdown of the Presentation Slide by Slide:

Slide 1: Laws governing the movement of planets in our solar system
Presented by the instructor at MBOU “Ust-Mayskaya School”.
Located in Ust-Maya settlement, RS (Ya), Ivanova N.A.

Kepler’s First Law states that every planet orbits the Sun in an elliptical path, with the Sun located at one of the foci of the ellipse. The eccentricity of the orbit, denoted by e, determines the shape of the ellipse. The center of the ellipse is represented by point O. Point A represents the perihelion, the closest point to the Sun, while point B represents the aphelion, the farthest point from the Sun. The distance OA or OB is the major semi-axis of the ellipse, and SA and SB represent the distances from the perihelion and aphelion to the center of the ellipse, respectively. The diagram below shows the positions of the Sun (S), the center of the ellipse (O), and the points A and B representing the perihelion and aphelion, respectively.
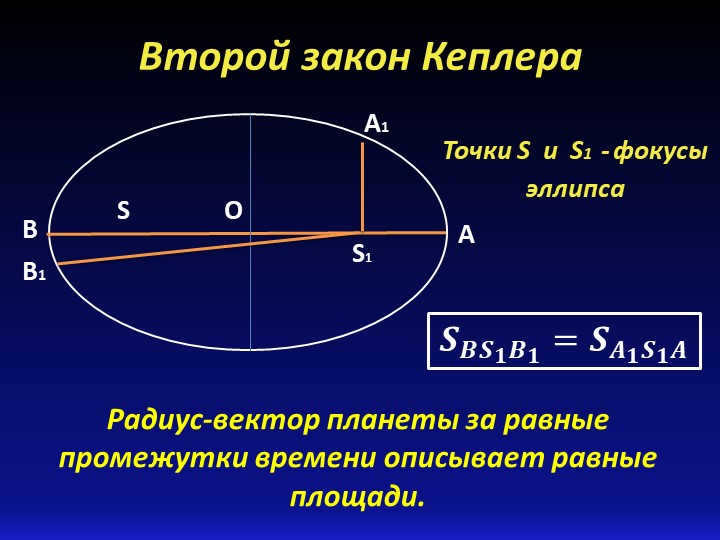

The third slide of Kepler’s Second Law states that the radius-vector of a planet describes equal areas in equal time intervals. In other words, as the planet moves around its orbit, it sweeps out equal areas in equal amounts of time. This can be represented by the equation S1B1 / SB = S1A1 / SA, where S and S1 are the focuses of the ellipse.
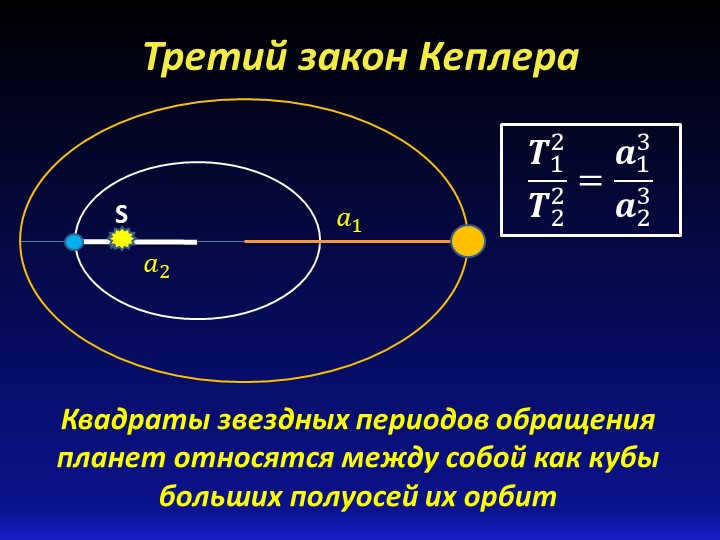

Slide 4: Kepler’s Third Law
The squares of the periods of the orbits of the planets are related to each other as the cubes of the major semi-axes of their orbits
T1^2 / T2^2 = a1^3 / a2^3
S
a1
a2
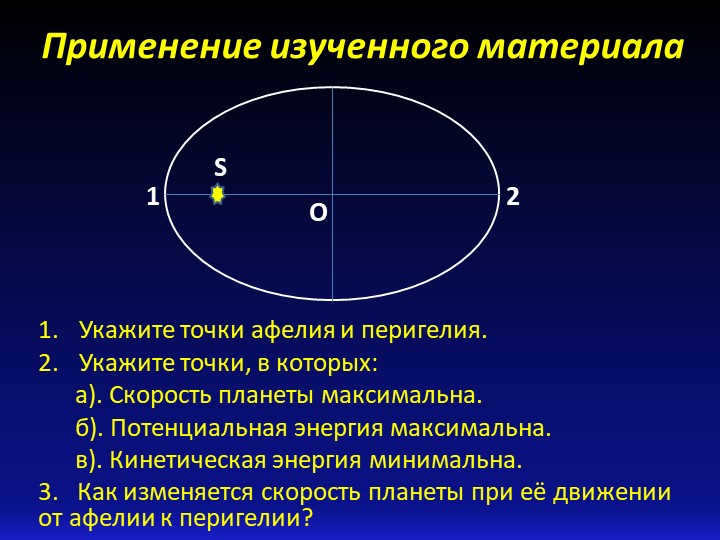
Slide 5: Application of the acquired knowledge
Indicate the locations of aphelion and perihelion.
Identify the locations where:
a). The planet reaches its highest velocity.
b). The potential energy is at its maximum.
c). The kinetic energy is at its minimum.
3. How does the velocity of a planet change as it moves from aphelion to perihelion?
S
О
1
2

6th slide Applying the acquired knowledge
Determining the orbital period of asteroid Belorussia with a major semi-axis of its orbit a=2.40 a.u.
The orbital period of Jupiter around the Sun is T=12 years. What is the average distance between Jupiter and the Sun?
The average distance between the Earth and the Sun
1 astronomical unit (a.u.) = 150 million kilometers.

Slide 7 Generalization and systematization
The boundaries within which Kepler’s laws can be applied:
– Kepler’s laws can be used to describe the motion of the planets, but they do not provide an explanation for the causes of motion;
– They allow for the calculation of the relative distances between the planets and the Sun;
– These laws are also applicable to the motion of the planets’ natural and artificial satellites, as well as the motion of other celestial bodies such as asteroids, comets, and stars in double systems.


Slide 8: The significance of Kepler’s laws:
– Confirmed the heliocentric system of Copernicus’ world order.
– Overcame speculative conclusions about the circular motions of celestial bodies by relying on empirical data.
– Introduced the concept of the astronomical unit as the basis for calculating various astronomical distances in the solar system.
– Served as the foundation for the discovery of other laws, such as the Titius-Bode law.

10 slide Resources used:
1. Kepler System cone model
Source (www.ck12.org)
2. Kunash M.A. Astronomy. 11th grade. Methodical manual to the textbook B. A. Vorontsov-Vel’yaminov, E. K. Strauta “Astronomy. Basic level. 11th grade” /
M. A. Kunash. – Moscow : Drofa, 2018. – 217, [7] c.
Brief document overview:
This presentation unveils Johannes Kepler’s laws of planetary motion within the solar system. It discusses various aspects of the ellipse, such as its center, major semi-axis, eccentricity, and focuses. Furthermore, it introduces key concepts like perihelion, aphelion, and astronomical unit. The presentation also delves into the limitations of Kepler’s laws and their significance. It showcases the different stages of comprehending the material and applying it to problem-solving scenarios.
The planets orbit the Sun, and those that are closer to the Sun move at a faster pace compared to those that are farther away. For example, Mercury completes one revolution around the Sun in just 80 Earth days. If Jupiter were to move at the same speed, it would complete a full revolution in 3.5 Earth years, whereas it actually takes 12 Earth years. Additionally, all planets have their own motion relative to other planets, and some even appear to move in a backwards direction. This phenomenon occurs because the Earth is catching up with them. During Kepler’s time, these “retrograde” motions were a great mystery to astronomers. It was through the resolution of this mystery that Kepler was able to formulate his three laws of planetary motion.
“I was suddenly struck by the realization that this tiny blue sphere was the Earth. I covered one eye with my thumb and closed the other, and my thumb completely blocked out the entire Earth. In that moment, I didn’t feel like a giant. I felt incredibly small.” Neil Armstrong, b. 1930
Johannes Kepler, born in 1571 and passed away in 1630, was a renowned figure in the field of astronomy.

Structure of polyhedra
The search for repetitive patterns in nature was undertaken by Johannes Kepler, a mathematician from Germany. Kepler lived during the transition from the sixteenth to the seventeenth century, a time when astrology held significant influence and astronomy was still in its early stages of development. In this era, religious beliefs were seen as crucial for uncovering the laws of nature, and observations alone were not sufficient. Drawing upon his mystical beliefs, Kepler postulated that the fundamental structure of the universe was constructed using flawless geometric shapes. Consequently, he devoted himself to identifying patterns in nature that could be linked to regular polyhedra.
Kepler came after Nicolaus Copernicus, a Polish astronomer, who proposed that the Sun was at the center of the universe and that the Earth revolved around it, contrary to the previous belief that the Sun and stars revolved around the Earth. This belief had been held since the time of the ancient Greek philosopher Ptolemy, who thought that the celestial bodies moved on the surface of solid crystal spheres. Copernicus was cautious about publishing his revolutionary ideas during his lifetime and only requested a colleague to do so shortly before his death. Copernicus’s assertion that the Earth was not the center of the universe, challenging the notion that humans were the most significant beings in it, protected by a God with a human focus, intrigued many people.

Kepler embraced Copernicus’s heliocentric theory, but he maintained the notion that the planets revolved around the sun in circular paths. He envisioned a system where the planets’ orbits were contained within a series of concentric spheres, with the distances between them determined by mathematical relationships based on the dimensions of three-dimensional geometric shapes inscribed within these spheres. His mind was captivated by polyhedrons inscribed within the spheres, with an increasing number of faces. The fundamental concept was that the laws of nature adhered to the fundamental geometric ratios discovered by the ancient Greeks.
The term “planet” is derived from the Greek word for “wandering.” Due to their proximity to Earth compared to distant stars, the planets in our solar system appear to move across the sky in a wandering manner. Every night, these planets navigate their way among the stars. However, at times, each planet undergoes a reversal in its path, resulting in a small loop. These retrograde movements were historically seen as unfavorable omens. The Ptolemaic model of planetary motion failed to explain such behavior, leading astronomers to introduce “epicycles” or additional loops to the planets’ orbits. Nevertheless, the epicycles proved to be inadequate as well. Copernicus’s heliocentric model of the universe required fewer epicycles compared to the geocentric model, but neither model accurately accounted for the intricate details.
"We, as a highly advanced clan of primates, inhabit a minuscule planet revolving around a rather ordinary star. However, our distinguishing feature lies in our capacity to comprehend the vastness of the cosmos, rendering us exceptionally unique beings." Stephen Hawking, 1989.
Kepler, in his pursuit to validate his geometric concepts through the meticulous examination of planetary trajectories, made use of the intricate tables of celestial motion meticulously compiled by Tycho Brahe. In this process, he stumbled upon recurrent patterns within these numerical arrays, eventually leading him to the formulation of his three fundamental laws.
The initial groundbreaking revelation by Kepler was his comprehension of the peculiar retrograde motion exhibited by Mars. Kepler astutely discerned that the phenomenon of backward loops could be explained if the planets orbited the Sun in elliptical, rather than perfectly circular, paths. The irony of this realization was profound: nature does not adhere to flawless geometric configurations.
Elliptical Orbits
In accordance with Kepler’s initial principle, a planet’s path can be described as an elliptical orbit with the Sun positioned at one of its foci.
Kepler’s second law explains the velocity of the planets as they orbit. The planets traverse equal areas in equal time intervals. The area is measured by the angle between the Sun and the two positions of a planet in its orbit (AB or CD) and resembles a slice of a circular cake. Due to the elliptical shape of the orbits, planets closer to the Sun must travel a greater distance to cover the same area that a more distant planet covers in the same amount of time. Consequently, the closer a planet is to the Sun, the faster it must move. Kepler’s second law establishes a correlation between the distance separating a planet from the Sun and its speed of motion. The Sun’s gravitational force imparts greater acceleration to a planet in proximity, though Kepler could not have been aware of this, naturally.
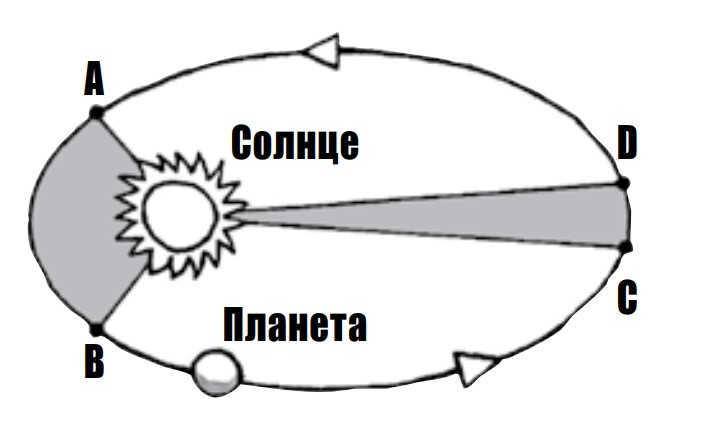
Kepler’s third law introduces the concept of the relationship between a planet’s orbital period and its distance from the Sun. This law states that the square of a planet’s orbital period is proportional to the cube of the long axis of its orbit. In simpler terms, the longer the elliptical orbit, the longer the time it takes for the planet to complete one revolution around the Sun. For example, if a planet is located twice as far from the Sun as Earth, it would take eight Earth years for it to complete one orbit. This implies that planets farther from the Sun move at a slower pace compared to those closer to it. As an illustration, Mars takes almost two Earth years to orbit the Sun, Saturn takes 29 Earth years, and Neptune takes a staggering 165 Earth years.
“Before I measured the heavens, Now I measure the shadows, My mind has gone to the sky, My body lies in the earth” Kepler’s epitaph, 1630.
Kepler’s formulation of his three laws enabled him to accurately describe the orbits of all the planets within our solar system. These laws also have broader applications, encompassing the motion of various celestial bodies such as comets, asteroids, and satellites around planets in our solar system, as well as planets orbiting other stars and even man-made satellites revolving around Earth. Kepler was able to consolidate these principles into geometric laws, although he was not aware of the underlying reasons behind their validity. Kepler believed that these laws were founded upon inherent geometric regularities that exist in nature. It was not until Newton came along that these laws were unified into the theory of universal gravitation.