Astronomy is a scientific field that, like any other, has its own unique vocabulary or jargon. To those unfamiliar with the subject, this jargon may seem like a meaningless collection of phrases, sometimes even eliciting a smile. For instance, we have terms such as “star’s brilliance,” “star’s luminosity,” and “star’s brightness.” At first glance, it may seem that these are just different ways to describe how bright or dim a star appears. However, are these terms truly synonymous, or do they carry distinct meanings? Let’s delve deeper into this matter.
What is the radiance of a celestial body?
Let’s begin with radiance. We have all come across statements like “the radiance of a star is equivalent to…” or “the radiance of the star surpasses that of the planet Saturn”. It may sound a bit peculiar, doesn’t it? A polished nickel can radiate, a copper basin in the sunlight, the buttons on a suit of armor can radiate. Even eyes can radiate. But a celestial body? There appears to be something absurd and somewhat antiquated in the phrase “star radiance”.
In reality, the term “star’s radiance” is not an outdated expression, but rather the most current and contemporary term. When astronomers refer to radiance, they are referring to the illumination that a celestial object (such as a star) emits on a plane perpendicular to the line of sight.
Is it too complex? No worries, it’s actually quite straightforward: the greater the brightness of a star, the more it lights up our eyes, and the clearer we can see it! Stars with high brightness are easily visible at night, and we often comment on them with awe: “What brilliant stars!” On the other hand, stars with low brightness are difficult to see, or even invisible, without the aid of a telescope. We refer to these stars as dim.
As the concept of brightness in astronomy has a precise scientific definition, it can be quantified.
Indeed, the brightness of stars (and any other celestial bodies) is measured using stellar magnitudes. Stellar magnitude is a unique dimensionless physical quantity that is exclusively used in the field of astronomy and astrophysics. It is represented by the Latin letter m followed by its numerical value. For instance, the brightness of Sirius is -1.44 m. Stellar magnitudes are measured in a paradoxical manner: the lower the m value, the higher the brightness of the celestial object. Find more information in the article “What is a stellar magnitude?”.
In addition to stellar magnitudes, the luminosity of celestial bodies can also be measured using conventional physical quantities, such as lux. The relationship between stellar magnitude and lux can be described as follows:
Therefore, the star Vega, with an apparent luminosity of approximately 0 m, generates an illuminance of 0.00000254 lux. The full Moon generates an illuminance of 0.25 lux.
Stars’ Luminosity
Earlier, I mentioned that we refer to stars with high luster as being bright. Does this imply that the concepts of brilliance and brightness are synonymous when describing celestial luminaries?
No! Brightness refers to the amount of light emitted from an object per unit area. Therefore, the term brightness is only applicable to objects that have a certain size – such as the Sun, Moon, planets (even in a small telescope, they appear as visible disks!), comets, and nebulae. The term brightness, however, cannot be used to describe point stars or meteors, as they do not have a measurable size and, therefore, no area! However, the term brilliance can be used to characterize the luminosity produced by any celestial body, whether it be a nebula or a star.
Why are stars referred to as bright? This is simply a result of an outdated expression that has been inherited from the past, when astronomers used the term brilliance to describe the overall brightness of celestial objects. What is now considered brightness was then referred to as surface brightness.

The photograph captures a stunning view of the starry sky and the Milky Way during the summer season. Countless stars of varying brightness can be seen, creating a mesmerizing sight. When it comes to the Milky Way, it is appropriate to discuss the brightness of its individual components. The photo credit goes to James Neeley.
The Concept of Luminosity
Now, let’s delve into the final term – luminosity. What exactly does it mean?
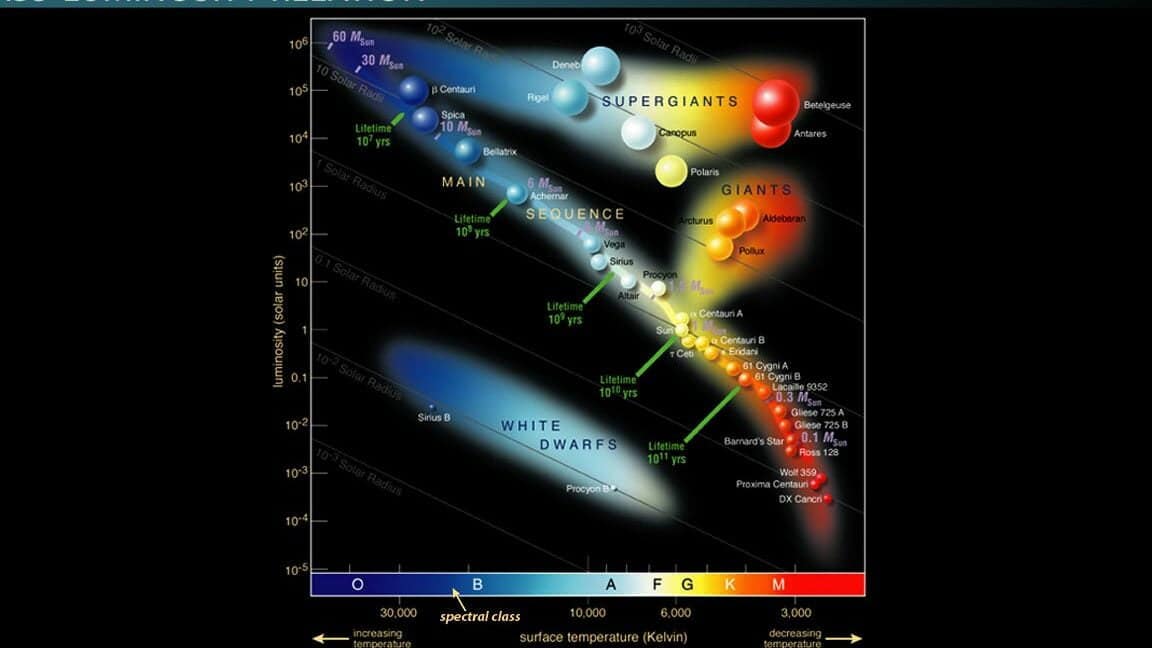
Luminosity refers to the amount of radiation emitted by a celestial body. To put it simply, it represents the total quantity of light that a celestial object, such as a star, emits in a given unit of time. Similar to the luminosity of a regular light bulb, the luminosity of stars is measured in watts. However, due to the immense magnitudes involved, astronomers often measure the luminosity of stars by comparing it to the luminosity of the Sun, which serves as a benchmark for the radiation power of other stars.
Let’s examine a few of the shining stars that can be seen in the evening sky during the month of February, for instance. Let’s consider Sirius, which happens to be the most luminous star in the entire night sky, and also the star Rigel in the Orion constellation. It is evident that Sirius is a more brilliant star than Rigel because it appears brighter to the human eye and emits a greater amount of light. Its apparent magnitude (m) is -1.47! On the other hand, Rigel does not possess the same level of brightness in our sky; its luminosity measures 0.12 m.

In this image, the star Rigel (also known as beta Orion) and its surrounding area can be seen. Rigel stands out as the brightest star, while the background stars appear much dimmer in comparison. However, it is important to note that only the brilliance of these stars can be measured, not their overall brightness. This is why astronomers often refer to stars based on their varying levels of brilliance. The photo was captured by Fred Espenak.
Now, the question arises: is Sirius a star with a higher luminosity than Rigel?
So, in summary, if we consider the brightness of a star as an indication of its intensity in the sky, the luminosity provides information about the actual power of the star’s radiation. The luminosity is directly given to us, but in order to calculate it, we need to know the distance to the star. It’s important to note that the term “luminosity” is applicable only to extended objects and not to stars, meteors, asteroids, or brown dwarfs.
When discussing celestial bodies in astronomy, specific terms such as stellar magnitude or color index are often used to describe their color and brightness.
Stellar magnitude is a measurement used to determine the brightness of a star or any other astronomical object.
There are two categories of stellar magnitudes – apparent and absolute.
Apparent magnitude defines the brightness that is visible to us. It represents the conditions under which the object can be observed from Earth.
This magnitude originated in the 2nd century BC when Hipparchus proposed dividing all stars into six magnitudes based on their brightness – the brightest and most visible stars were classified as first magnitude stars, while the dimmest were classified as sixth magnitude stars.
However, this subjective approach is not applicable for modern purposes, especially considering that most astronomical objects cannot be seen with the naked eye. Nevertheless, the concept of apparent brightness remains highly useful. Therefore, Hipparchus’ classification has been modernized to become more measurable and objective, while still maintaining the original classes established by Hipparchus.


If star 1 has an apparent brightness of b1, and star 2 has an apparent brightness of b2, the difference in magnitudes can be calculated using the following expression:
We can also define the ratio by comparing the brightness of the two stars:

However, the situation is not as straightforward as it may seem. When a star or any other object emits or reflects light, it does so at various wavelengths, and our perception of these wavelengths differs. For instance, green light appears brighter to us, while red light appears dimmer. And, of course, we cannot perceive infrared light at all.
The distance from the observer, r, affects the perceived brightness and magnitude of a star. To eliminate this distance factor, the concepts of absolute brightness and absolute magnitude were introduced.
The absolute brightness, or luminosity, of a star (L) is the brightness it would have if it were located 10 parsecs away from the observer.
Since luminosity decreases in proportion to the square of the distance, the absolute brightness (L) and the apparent brightness (l) are related by the following equation:
m represents the observed stellar magnitude, while M represents the intrinsic stellar magnitude, which is defined as the magnitude a star would have if it were situated at a distance of 10 parsecs.
Using the ratio mentioned above, we can derive the following equation:
M = m + 5 – 5lg r
When accounting for interstellar absorption:
Where A(r) represents the amount of light absorbed based on the distance from the star.
This equation enables us to determine the absolute magnitude of a star if we know the distance, or to calculate the distance if we know the absolute magnitude, using the formula:
lg r = (m – M)/5 + 1
Absolute stellar magnitudes can be categorized as bolometric, visual, or photographic.
The Sun has an absolute stellar magnitude of +4.7 m.
The luminosity of a star is often expressed as the ratio of its absolute luminosity to that of the Sun.
The brightest stars are 14 m brighter than the Sun, emitting energy at a rate 1,000,000 times greater. The faintest stars are 14 m dimmer, emitting 300,000 times less energy.
The ratio of luminosities between the brightest and faintest stars can reach approximately 100 billion.
Imagine being out at sea on a dark night and seeing a faint light flickering in the distance. Without the guidance of an experienced sailor, it’s difficult to determine whether it’s a lantern on a passing boat or the powerful searchlight of a distant lighthouse.
This same uncertainty applies when we gaze up at the night sky and see the stars twinkling. The apparent brightness of a star is not solely determined by its true luminosity, also known as its luminosity , but also by its distance from us. Knowing the distance to a star allows us to calculate its luminosity relative to the Sun. For example, a star that is actually ten times dimmer than the Sun would have a luminosity value of 0.1.
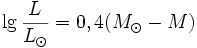
There is another method to express the true brightness of a star. It involves calculating the stellar magnitude it would have if it were located at a standard distance of 32.6 light years from us. This distance is defined as the point where light, traveling at a speed of 300,000 km/sec, would take exactly that amount of time to reach the star.
![]()
The equation for calculating the luminosity of a star can be expressed as follows: L = 4πR²T⁴, where R represents the radius of the star and T represents the temperature.
Utilizing this standardized distance has proven to be advantageous in various calculations. The brightness of a star, much like any other source of light, diminishes as the square of the distance from it increases. This principle enables us to determine the absolute magnitudes or luminosities of stars by having knowledge of their respective distances.
Once the distances to the stars became known, we were able to calculate their luminosities, allowing us to arrange them in a line and compare them under the same conditions. It is worth acknowledging that the results were astonishing, as it had previously been assumed that all stars were similar to our Sun. The luminosities of the stars turned out to be remarkably diverse, and they cannot be compared to any ranks of pioneers.
Let’s consider only extreme examples of luminosities in the world of stars.
The dimmest star known for a long time was a star that is 50 thousand times less bright than the Sun, with an absolute luminosity value of +16.6. However, even dimmer stars have been discovered since then, whose luminosity, compared to the Sun, is millions of times lower!

The perception of size in space can be deceiving. From Earth, Deneb appears brighter than Antares, but the Pistol Star is not visible at all. However, both Deneb and Antares appear insignificant compared to the Sun. This misconception can be illustrated by a simple fact: the Pistol Star emits the same amount of light in one second as the Sun does in a whole year!
On the opposite end of the star spectrum is the Goldfish Star. This star is only visible in the Southern Hemisphere without the aid of a telescope, and it appears as an eighth magnitude star. However, in reality, the Goldfish Star is 400,000 times brighter than the Sun, with an absolute luminosity value of -8.9.
If we consider the brightness of the Sun as the brightness of an ordinary candle, then the “S” of the Goldfish would be like a powerful searchlight in comparison, and even the faintest star is weaker than the most insignificant firefly.
Therefore, stars are distant suns, but their light intensity can vary greatly from that of our own luminary. Metaphorically speaking, exchanging our sun for another would require caution. With the light of one, we would be blinded, while with the light of the other, we would wander in twilight.
- You are currently on:
- Home
- 11th grade
- Astronomy
- Measuring the brightness of stars
In the field of astronomy, specific terms are sometimes used to describe the color and brightness of celestial bodies, such as stellar magnitude or color index.
Stellar brightness is a measurement that indicates the luminosity of a star or any other celestial object.
There are two types of stellar brightness – apparent and absolute.
Apparent brightness indicates the luminosity that we perceive or can perceive. In other words, it depends on the conditions of observation from Earth.
This scale of measurement dates back to the II century BC, when Hipparchus proposed dividing all stars into six magnitudes based on their brightness – the brightest and most easily visible stars were classified as first magnitude, while the dimmest were classified as sixth magnitude.
Undoubtedly, the subjective method is not suitable for contemporary needs, especially considering that the majority of celestial bodies cannot be observed without the aid of instruments. Nevertheless, the concept of apparent brightness remains highly valuable. Consequently, in the present era, Hipparchus’ classification system has been updated to be more precise and objective. Remarkably, despite the revisions, the original classes devised by Hipparchus have been retained.


If the apparent brightness of star 1 is represented by b1, and the apparent brightness of star 2 is represented by b2, the difference in magnitudes can be calculated using the following expression:
Furthermore, we can define the ratio by considering the concept of brightness ratio:

However, the situation is not as straightforward. When an object, such as a star, emits or reflects light, it does so at various wavelengths, which are perceived differently by humans. Even when the intensity is the same, we perceive green light as being brighter, red light as being dimmer, and infrared light is not perceived at all.
Uniqueness of Absolute Stellar Magnitudes
The apparent brightness and apparent magnitude of a star are influenced by its distance from the observer, denoted as r. To eliminate the impact of distance, we introduce the concept of absolute brightness and absolute magnitude of a star.
The absolute luminosity of a star, denoted as L, is the luminosity it would have if it were placed at a distance of 10 parsecs from the observer.
As the luminosity decreases inversely proportional to the square of the distance, the absolute luminosity L and the apparent luminosity l are related by the following equation:
L/l = r^2/100 = 2.512 m-M
m represents the observed magnitude of the star, while M represents its intrinsic magnitude, which is defined as the magnitude the star would have if it were located 10 parsecs away.
Using the ratio given above, we can derive the following formula:
M = m + 5 – 5lg r
Considering the impact of interstellar absorption:
M = m + 5 – 5lg r – A(r)
where A(r) represents the light absorption that is directly proportional to the distance to the star.
This equation enables us to determine the absolute stellar magnitude of a star when the distance is known, and to determine the distance when the absolute magnitude is known, by employing the following formula:
Absolute magnitudes of stars can be measured using bolometric, visual, and photographic methods.
The Sun has an absolute magnitude of +4.7 m.
The luminosity of a star is often expressed as the ratio of its absolute luminosity to that of the Sun.
The most luminous stars are 14 m brighter than the Sun and emit 1,000,000 times more energy. The least luminous stars are 14 m fainter and emit 300,000 times less energy.
The ratio of luminosities between the brightest and faintest stars is approximately 100 billion.
The brightness (radiance) of celestial bodies
Picture a gentle flickering light somewhere in the vastness of the ocean during the obscurity of night. Unless a seasoned sailor elucidates its nature, one might mistake it for a lantern adorning the bow of a passing vessel or the powerful beam of a distant lighthouse.
We find ourselves in a similar conundrum on a moonless night when gazing at the shimmering stars. Their apparent radiance is contingent upon their true luminous intensity, known as brightness, as well as their distance from us. Only by discerning the star’s distance can we accurately ascertain its brightness relative to the Sun. For instance, a star that is ten times dimmer than the Sun would be expressed as having a brightness value of 0.1.
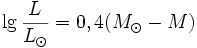
An alternative method of expressing the actual brightness of a star is to determine its apparent magnitude at a standardized distance of 32.6 light years. This means that if the star were located at this distance, it would appear to us with a certain brightness, taking into account the time it takes for light to travel at a speed of 300,000 km/sec.
![]()
where R represents the star’s radius and T represents its temperature.
Using this standardized distance has proven to be convenient for a variety of calculations. The brightness of a star, similar to any source of light, changes in inverse proportion to the square of the distance from it. This principle enables us to determine the absolute stellar magnitudes or luminosities of stars by having knowledge of their distances.
Allow us to present some exceptional instances of luminosities in the realm of stars.
The least luminous star that has been documented for an extended period of time is a star that is 50 thousand times dimmer than the Sun, with an absolute luminosity value of +16.6. Nevertheless, subsequently, even more dim stars have been unearthed, whose luminosity, in contrast to the Sun, is millions of times lower!

The size of objects in outer space can be deceiving. For example, from Earth, Deneb appears brighter than Antares, but the Pistol star is not visible at all. However, both Deneb and Antares appear insignificant compared to the Sun. This misconception is proven wrong by a simple fact: the Pistol star emits as much light in one second as the Sun does in an entire year!
On the other end of the spectrum, there is the S of Goldfish, which is only visible in the countries of the Southern Hemisphere of the Earth. Without a telescope, it appears as a star of the eighth magnitude. However, in reality, it is 400 thousand times brighter than the Sun and has an absolute luminosity value of -8.9.
The Sun’s absolute luminosity is +5, which is relatively low. If we were 32.6 light years away, we wouldn’t be able to see it clearly without binoculars.
If we compare the brightness of the Sun to that of an ordinary candle, the “S” of the Goldfish would be like a powerful searchlight, while the faintest star would be weaker than the tiniest firefly.
Stars are essentially distant suns, but their light intensity can vary greatly from our own. Swapping our Sun for another would require caution. One might blind us with its brightness, while another would leave us in twilight.
- You are here:
- Home
- Astronomy
- Measuring the brightness of stars

Stellar magnitude is a unique numerical value that represents the brightness of a star or other celestial body in relation to its visible area. Put simply, this magnitude indicates the amount of electromagnetic waves emitted by the body that can be detected by an observer. As a result, the magnitude is influenced by the characteristics of the observed object as well as the distance between the observer and the object. It is important to note that this term specifically refers to the visible, infrared, and ultraviolet spectra of electromagnetic radiation.
The terms “brilliance” and “brightness” are also employed to describe point light sources and extended light sources, respectively.
Hipparchus of Nicaea, an ancient Greek scientist who resided in Turkey during the 2nd century BC, is widely regarded as one of the most influential astronomers of the ancient world. He meticulously assembled an extensive catalogue of stars, marking the beginning of such astronomical documentation in Europe. This catalogue provided detailed descriptions of over a thousand celestial luminaries. Additionally, Hipparchus introduced the concept of stellar magnitude. By observing the stars with the unaided eye, the astronomer devised a system to classify their brightness into six magnitudes. In this system, the first magnitude represented the brightest objects, while the sixth magnitude denoted the dimmest stars.
In the 19th century, the British astronomer Norman Pogson made enhancements to the scale for measuring stellar magnitudes. He expanded the range of values and introduced a logarithmic correlation. This means that for every increase of one in stellar magnitude, the brightness of the object decreases by a factor of 2.512. Therefore, a star with a magnitude of 1 (1m) is a hundred times brighter than a celestial body with a magnitude of 6 (6m).

The brightness of Vega, the brightest star in the constellation Lyra, served as the initial benchmark for the celestial luminary with a stellar magnitude of zero. Later on, a more precise definition was established – an object with zero stellar magnitude should have an illuminance of 2.54-10 -6 lux and a light flux in the visible range of 10 6 quanta/(cm²-s).
Observable brightness of stars
The characteristic mentioned above, initially defined by Hipparchus of Nicaea, later became known as “visible” or “visual”. This means that it can be detected by the human eye within the visible range, as well as by various instruments such as telescopes, which can detect light in the ultraviolet and infrared ranges. The stellar magnitude of the Big Dipper constellation is 2 m. However, we are aware that Vega, despite having a luminosity of zero (0 m), is not the brightest star in the sky (it is the fifth brightest in terms of luminosity, and the third brightest for observers from the CIS region). Therefore, brighter stars can have a negative stellar magnitude, such as Sirius (-1.5 m). Additionally, it is now known that celestial objects can include not only stars, but also bodies that reflect the light of stars, such as planets, comets, or asteroids. The stellar magnitude of the full Moon is -12.7 m.
To facilitate the comparison of the true brightness of celestial bodies, scientists have devised a characteristic known as absolute stellar magnitude. This metric calculates the apparent stellar magnitude of an object as it would appear if it were located 10 parsecs (equivalent to 32.62 light years) away from Earth. By using this standardized distance, the comparison of different stars is not influenced by the observer’s proximity.
For celestial objects within our Solar System, the absolute stellar magnitude is determined using a different distance measurement. Specifically, it utilizes the distance from the object to the observer, which is 1 astronomical unit. Theoretically, the observer would be positioned at the center of the Sun.
Resources about the subject

Luminosity has emerged as a more contemporary and valuable measurement in the field of astronomy. It serves to quantify the total energy released by celestial objects during a specific timeframe. The absolute stellar magnitude is employed in the determination of this parameter.
Spectral dependency
As previously mentioned, the measurement of stellar magnitude varies across different types of electromagnetic radiation, resulting in different values for each section of the electromagnetic spectrum. Astronomers can utilize photographic plates to capture images of cosmic objects, which are particularly sensitive to the high-frequency portion of visible light, causing stars to appear blue in the resulting image. This specific measurement of stellar magnitude is referred to as “photopic” magnitude, denoted as mPv. In order to obtain a value that closely aligns with the visual perception of brightness (“photovisual” magnitude, mP), the photographic plate is coated with a specialized orthochromatic emulsion and a yellow light filter is utilized.

A photograph of the Sun taken using a dark light filter.
Researchers have created a photometric system of ranges to analyze various features of celestial bodies, including surface temperature, light reflection (excluding stars), and light absorption in interstellar space. To do this, they capture images of the Sun using different electromagnetic spectra and compare the results. The most commonly used filters for these photographs are ultraviolet, blue (for measuring stellar magnitude), and yellow (similar to the photovisual range).
A photograph containing the captured energies of all different types of electromagnetic waves is used to determine the bolometric stellar magnitude (mb). This measurement is essential for astronomers to calculate the luminosity of celestial bodies, taking into account their distance and the amount of interstellar absorption.
Stellar magnitudes of specific objects
- The Sun has a stellar magnitude of -26.7 m.
- The Full Moon has a stellar magnitude of -12.7 m.
- The Iridium Flash, which occurs when sunlight is reflected from the surface of one of the 66 satellites in the Iridium system, has a stellar magnitude of -9.5 m. These satellites are used for transmitting voice and data, and during certain periods, they create a bright, smooth flash in the sky that lasts for up to 10 seconds.

- The most intense explosion of a supernova occurred in 1054, leading to the formation of the Crab Nebula and reaching a brightness of -6.0 m. According to historical accounts from Chinese and Arab astronomers, this supernova remained visible for 23 days and could even be seen during daylight hours without the aid of any instruments.
- Venus at its maximum brightness is recorded as -4.4 m.
- From the perspective of an observer on the Sun, the Earth has a brightness of -3.84 m.
- Mars reaches a maximum brightness of -3.0 m.
- Jupiter has a maximum brightness of -2.8 m.
- The International Space Station (ISS) reaches a maximum brightness of -2 m.

The International Space Station is currently visible against the backdrop of the famous Big Dipper constellation.
- The brightness of α Centauri is -0.27 m.
- Vega has a brightness of +0.03 m.
- The Andromeda Galaxy has a brightness of +3.4 m.
- Faint stars, still visible to the human eye, have a brightness ranging from +6 m to +7 m.
- Proxima Centauri has a brightness of +11.1 m.
- The brightest quasar has a brightness of +12.6 m.
- Objects detectable with ground-based telescopes (8-meter telescopes) have a brightness of +27 m.
- Objects detectable with the Hubble Space Telescope have a brightness of +30 m.
- Homepage
- Astronomical Objects
The Radiance and Luminosity of Celestial Bodies
When observing the heavens, one is immediately captivated by the variations in the brilliance of celestial bodies.
The most luminous star in the nocturnal firmament, Sirius (α Canis Majoris), already slightly above the horizon, enthralls us with its radiance, while its neighboring stars only become visible at a considerably higher altitude (3-5°).
The stars of the Ursa Major constellation are easily discernible even in an urban sky during a full moon, and outside of urban areas on a moonless, clear night, the unaided eye can discern several thousand stars in the heavens.
Upon gazing at the sky through binoculars, one quickly realizes that there are numerous stars whose luminosity is too faint for the naked eye to perceive.
In ancient times, astronomers attempted to quantify differences in star brilliance using numerical values. Stars were classified into six categories known as stellar magnitudes.
The brightest stars were classified as first magnitude stars, followed by slightly dimmer stars known as second magnitude stars, and so on. The faintest stars visible to the naked eye (as telescopes had not yet been invented) were referred to as sixth magnitude stars.
This system of categorizing stars by brilliance is commonly attributed to Hipparchus (2nd century BC), who first implemented this classification in his star catalog. Therefore, when we refer to “stellar magnitude,” we are referring to the brightness of the star, not its size.
All stars, regardless of their brightness, have always appeared as luminous points without any discernible size to astronomers.
We can only speculate about the motivations of the ancient scientists who chose to establish exactly six groups, or magnitudes, for stars. It is even more remarkable that the concept of stellar magnitude has endured in the field of science and continues to be employed by contemporary astronomers!
Naturally, the definition of stellar magnitude has evolved over time. It no longer refers to groups of stars with similar brightness.
The apparent brightness of a star, as observed from Earth, can be quantified by its apparent stellar magnitude.
What aspect of a star’s brilliance do we perceive as a physical quantity?
Scientific measurements indicate that our eyes perceive the light emitted by a star as its luminosity, which is the amount of light that falls on a unit area per unit time, perpendicular to the rays.
Our perception of the brightness is influenced by the psychophysiological Weber-Fechner law, which states that our perception of brightness changes in an arithmetic manner when the level of illumination changes exponentially.
This observation was made during the 19th century, but astronomers of ancient times unknowingly followed this principle: they categorized the stars into different magnitudes in such a way that the average ratio of brightness created by stars of the first and second magnitudes is almost exactly the same as the ratio of brightness from stars of the second and third magnitudes, and so on.
Contemporary astronomers have upheld this tradition, with some refinements: nowadays, the ratio of luminosities produced by celestial bodies with magnitudes differing by one is defined to be equal to 5 √100 = 2.5118864. ≈ 2.512.
The base-10 logarithm of this value (lg10 2/5 ) is precisely equal to 0.4.
Therefore, a ratio of luminosities equal to 100 corresponds to a difference in luminosity of exactly 5 stellar magnitudes.
To keep it concise, the term “stellar magnitude” is represented by the upper index m (from Latin magnitudo – magnitude) after the corresponding number. For instance, an astronomer would express “5 stellar magnitudes” as 5 m.
By taking a certain star as a reference point and assigning it a specific stellar magnitude (which is generally arbitrary), it becomes possible to compare the light flux of all other stars to it and determine their stellar magnitudes.
If L1 and L2 represent the luminosities of the first and second stars, and m1 and m2 represent their stellar magnitudes, then
The second formula indicates that the brighter the star, the smaller its stellar magnitude. This relationship is denoted by a minus sign. The coefficients in these formulas (2.512 and 2.5) are almost exactly the same, which is a result of chance. This is because lg(2.512) = 0.4 = 1/2.5.
By utilizing these formulas, it becomes possible to expand the concept of stellar magnitude to celestial objects that cannot be seen with the naked eye, no matter how faint they may be.
The magnitudes of stars that can be observed by space telescopes and the largest ground-based telescopes can reach up to 30 m.
It is important to note that stellar magnitudes are not always expressed as whole numbers. Modern ground-based instruments have the capability to measure star brightness to the nearest hundredth or even thousandth of a stellar magnitude. When observing outside the Earth’s atmosphere, the accuracy is even higher.
After conducting measurements, it was discovered that there are some stars with an exceptionally high luminosity, surpassing that of stars with a magnitude of one. To account for this, these stars were given zero or even negative stellar magnitudes. For instance, the luminosity of Sirius is recorded as -1.5 m.
Stellar magnitudes can be used to measure the brightness of not only stars, but also planets, the Moon, and the Sun – essentially, any celestial bodies. The luminosity of the Sun is estimated to be -26.8 m, while the full moon has a luminosity of -12.7 m.
With normal vision, the naked eye can see stars up to magnitude 6 in a dark sky. There are approximately 5000 of these bright stars in the entire sky, which are included in a special catalog. However, there are many more faint stars than bright stars. The U.S. Naval Observatory’s B1.0 catalog includes stars up to magnitude 21, and there are about a billion stars in total.
Up until now, we have been discussing visual stellar magnitudes that are measured by the human eye or by instruments that have the same relative sensitivity to different colors as the human eye.
However, the measurement of stellar magnitude can also be done using instruments that are more sensitive to different wavelengths of light than the human eye. As a result, the measurements can vary for stars that have the same visual brightness but different colors. (For example, the naked eye can easily perceive color differences between the white star Rigel and the red star Betelgeuse in the constellation Orion.) It is generally agreed that for white stars of spectral class A0, whose light is not affected by interstellar dust, the stellar magnitudes should be the same regardless of the instrument used for measurement.
When photography was first used in astronomy, it was observed that reddish stars appear much dimmer in photographs of the night sky compared to white and blue stars with the same visual brightness.
Some instruments are more responsive to red wavelengths and less responsive to blue wavelengths compared to the human eye. The measurements of red stars taken with these instruments result in numerically smaller magnitudes than the visual magnitudes.
To estimate the color of a star, we can compare its magnitudes captured by instruments that are sensitive to different parts of the spectrum. This is done by calculating the color index, which is the difference between the corresponding magnitudes. For instance, the color index (CI) can be determined by subtracting the photographic magnitude (mpg) from the visual magnitude (mv): CI = mpg – mv.
The color of stars can also be determined using a single instrument that is sensitive to a wide range of the spectrum. This can be done by placing different colored light filters in front of the instrument and taking light measurements through them. The commonly used filters are B (blue) and V (visual, which corresponds to yellow-green light).
In modern astrophysics, the color index (B-V) has replaced the CI value. The color index is calculated by measuring the difference in stellar magnitudes using B and V filters. A color index of zero indicates a white star, a negative value indicates a bluish star, and a positive value indicates a red star.
All the stellar magnitudes discussed so far (photographic, visual, B and V magnitudes) are visible stellar magnitudes. These magnitudes are obtained through observation from Earth and therefore reflect differences in distances to the stars more than the true differences in their radiative power.
Moreover, the expanse amidst the Earth and the celestial bodies is far from vacant – it comprises interstellar gas-dust formations that soak up light. Solely by considering the variance in the stellar distances and the extent of interstellar assimilation of their radiance, can we employ the observable stellar magnitudes to evaluate the authentic luminosity (radiative potency) of the stars.
Please take into consideration that the Earth’s atmosphere also plays a significant role in reducing the apparent brightness of stars. It filters out different colors of light to varying degrees, with blue light being more strongly attenuated and red light being less affected. The optical properties of the atmosphere vary depending on the observer’s location and the height of the star above the horizon, both of which influence the thickness of the air column that the light passes through. Additionally, the air quality at the observation site also affects these measurements. Astronomers must account for all these factors when making measurements and correct the apparent stellar magnitudes for the absorption of light in the Earth’s atmosphere. The stellar magnitudes provided in the tables are actually intended for an observer outside of the Earth’s atmosphere.
The Sun is our closest star. Among the other stars, the one that is closest to us is a triple system known as α Centaurus, consisting of a bright double star and its faint companion Proxima Centauri. Proxima Centauri is actually slightly closer to us than α Centaurus, which is why it is named “Proxima,” meaning “nearest” in Latin. This is a perfect example of how apparent luminosity is not solely determined by distance. Although Proxima is closer to us than α Centaurus, it appears fainter than each of its components by about 10 m. In fact, the distance from Earth to Proxima is approximately 267,000 astronomical units. As we can see, the astronomical unit is too small of a unit to measure distances to stars.
In popular science literature, the distance to stars is often described in terms of light-years, which is actually a measure of length rather than time. A light-year represents the distance that a beam of light travels in the span of one year. For instance, the distance to Proxima Centauri is approximately 4.2 light-years.
In professional astronomical literature, however, distances to stars are typically expressed in parsecs. A parsec is defined as the distance at which the radius of Earth’s orbit, when viewed from the star at a right angle, subtends an angle of one arcsecond. Since one arcsecond is equal to 1/206265 of a radian, it follows that 1 parsec is equivalent to 206,265 astronomical units or 3.26 light-years.
More generally, the angle at which the radius of Earth’s orbit is visible from a star is referred to as its parallax. The term “parsec” is simply a combination of “parallax” and “second”. Using parsecs as the unit of measurement, the distance to Proxima Centauri is approximately 1.3 parsecs.
The absolute brightness of a star is measured by its absolute stellar magnitude.
In order to determine the absolute magnitude (M) of a star from its apparent magnitude (m), it is important to calculate the magnitude the star would have if it were positioned at the standard distance of 10 pc from Earth, taking into account the absorption of light in interstellar space:
M = m + 5 – 5 – 5-lg r – A,
Where Μ represents the absolute magnitude of a star, m is the apparent magnitude, r represents the distance in parsecs, and A is the attenuation of the star’s luminosity due to interstellar light absorption, expressed in magnitudes.
When using this equation, it is important to remember that all three photometric magnitudes (M, m, and A) should be in the same system, whether it’s visual, photographic, B, V, or any other.
The absolute visual magnitude of the Sun is approximately +5. Therefore, if the Sun were located at a “standard” distance of 10 parsecs from us, it would be visible to the naked eye, but would appear among many other fifth magnitude stars. On the other hand, if Rigel (β of Orion) were brought closer to the “standard” distance, it would be a -7.5 m star, but there are no stars that bright in our night sky.