What is the velocity of the Earth’s rotation?

In order to comprehend the correlation between the Earth’s motion and natural phenomena, it is essential to ascertain the speed at which our planet orbits in space. Having knowledge of this value also enables us to make predictions about the future of this celestial body.

The Earth’s orbital path

Our planet traverses an elliptical trajectory around the Sun, periodically approaching the luminary at a distance of 147 million kilometers (this occurs during January each year) and subsequently moving away. The point nearest to the Sun is referred to as perihelion. After six months, the Earth reaches aphelion, which is when the distance from it to our star becomes equal to 152 million kilometers. The average distance is considered to be 150 million kilometers – this is known as the Earth’s large semi-major axis.

The orbit of Earth is oriented towards the east. In terms of a clock, it can be described as moving in a “counter-clockwise” direction.

The Earth completes a full revolution around the axis passing through the center of the solar system in slightly over 365 days, 5 hours, and 48 minutes. This period, known as the astronomical year, does not align with the calendar year, which is based on a whole number of days for convenience.

The Earth’s orbital path spans 942 million km. Through calculations, scientists have determined that the average speed of our planet’s motion around the sun is 29.8 km/s. However, this is an average value, as the Earth experiences slight deceleration and acceleration at its aphelion and perihelion points.

How fast does the Earth travel through the Universe?

In our solar system, all the planets orbit around the Sun, but the Sun itself is not stationary. Being a massive celestial object, it generates a powerful gravitational field that attracts nearby objects. This gravitational pull is what causes the Earth to move towards the outer boundaries of the neighboring constellations Lyra and Hercules, at a velocity of 20 kilometers per second.

Meanwhile, the Earth’s movement around its axis creates a unique and fascinating phenomenon. As the Earth spins, it also travels through the vast expanse of the universe. This cosmic journey is not a solitary one, as the Solar System and its celestial neighbors are all pulled towards the majestic constellation known as Serpentor. Serpentor, with its equatorial position and its intersection with the ecliptic, has witnessed the spectacular explosions of supernovae in our Galaxy. The speed at which the Earth travels during its rotation is approximately 15 km/s, while the journey towards Serpentor is even faster, reaching speeds of 23-25 km/s.

However, the Milky Way itself is not stationary:

• Both the Milky Way and its neighboring galaxy Andromeda in the Local Group are mutually attracting each other, traveling at a velocity of approximately 100-150 km/s;
• The nearby large galaxy M33 is also moving towards us at a similar speed;
• The massive Virgo cluster, located 15-20 light-years away, exerts such a strong gravitational pull on the Milky Way that it is being drawn towards it at a speed of 400 kilometers per second.

However, Andromeda, M33, and the Virgo cluster, which contains a staggering 1500 individual galaxies, are not stationary entities either. They are all hurtling through space at a velocity of 600 kilometers per hour towards the Great Attractor. The Great Attractor is the name given to a hypothetical point situated deep within the Universe, comprised of numerous superclusters that exert a gravitational pull on everything in their vicinity.

The velocity of Earth in space is determined by the collective influence of these factors.

Implications for Us

We may not perceive the movement of our planet, but if the Earth were to suddenly come to a halt, the consequences would be catastrophic. Our trajectory is determined by the gravitational pull of the sun and the planet’s own motion. Increasing the former by multiple magnitudes and/or decreasing the latter would result in the Earth plunging into the sun. Conversely, if the gravitational force from the sun were to disappear or significantly diminish, and the planet’s motion were to intensify, we would be at risk of being propelled tangentially into the vast expanse of space.

As for concerns about galaxies colliding in the near future, they are premature. The Milky Way’s velocity is relatively sluggish. It takes no less than 200-300 million years for it to move a distance equivalent to its own diameter.

After analyzing the Earth’s rotation on its own axis, we can now delve into its movement around the Sun and determine the velocity of this motion. Additionally, we will explore Kepler’s three laws, as they are fundamental to our understanding of this topic.

The initial approach

What is the speed at which the Earth orbits the Sun? The primary thought that arises is to utilize the well-known formula for determining linear velocity:

The distance from the Earth to the Sun is equivalent to one astronomical unit or 149,597,870,700 meters. The time it takes for a complete revolution is one year. When we convert this to seconds, we obtain 31,536,000 s.

Insert all of these values into our equation and compute.

m/s.

Another approach.

However, there is another method we can use. The velocity of the Earth can be calculated as the first cosmic velocity within the gravitational field of the Sun. Hence, we can recall the equation used to determine the first cosmic velocity.

Here, G represents the gravitational constant, R denotes the distance between the Earth and the Sun, and M signifies the mass of the Sun. All we need to do is measure the mass of the Sun and perform the necessary calculations:

The velocity of the Earth around its axis is approximately 29775.559 m/s.

For convenience, the speed is often rounded and represented as 30 km/s or 108 000 km/h. Interestingly, Hindus have a special fondness for the latter option. In Hinduism, the number 108 is considered sacred. They even defined Pi as a ratio of 339/108. But let’s get back to the velocity of the Earth.

Kepler’s primary principle

During our calculations, we made the assumption that the Earth follows a uniform path along a circular trajectory. However, in actuality, this approximation does not precisely reflect reality.

During the early 17th century, Johannes Kepler, a German astronomer, made a groundbreaking discovery about the movement of planets in our solar system. After analyzing years of observations collected by his mentor, Tycho Brahe, a Danish astronomer, Kepler concluded that planets do not follow a circular path but instead move along an ellipse. In this elliptical orbit, one of the foci is occupied by the Sun. This revolutionary idea became known as Kepler’s first law.

Kepler’s first law states that all planets in our solar system orbit the Sun along an elliptical path, with the Sun located at one of the focal points.

Now, let’s delve into the characteristics of an ellipse and understand the concept of its focus or focuses.

An ellipse is a geometric shape that consists of all the points in a plane for which the sum of the distances from each point to two fixed points, called the foci, is constant and greater than the distance between the foci.

Let’s illustrate this concept with a simple example. Imagine we have a piece of string with stationary buttons at each end. We stick the buttons into a piece of drywall that was leftover from a home renovation project.

Next, we take a pencil and draw lines while keeping the string taut. The resulting shape is an ellipse, and the locations where we stuck the buttons are referred to as the foci.

Primary and secondary semi-major axis

Crucial characteristics of the ellipse include its semi-major axis. This value is commonly represented by the Latin letter “a”, while the secondary axis is denoted by the letter “b”. Both are in Latin.

The primary semi-major axis refers to the distance from the center of the ellipse to its farthest point. Conversely, the secondary semi-major axis represents the distance from the center to the nearest point of the ellipse.

Eccentricity

Another important characteristic of an ellipse is known as eccentricity. It is commonly represented by the letter “e” and is defined as the ratio of the focal length of the ellipse (c) to the major semi-axis (a).

An ellipse is often referred to as a flattened circle, and the eccentricity indicates just how flattened the circle is.

The closer the eccentricity is to one, the more elongated the ellipse becomes. Conversely, an eccentricity close to 0 will result in an ellipse that closely resembles a circle. In fact, a circle can be considered as an ellipse with an eccentricity of 0.

In the solar system, Venus has the smallest eccentricity, measuring only 0.007, which means its trajectory is almost circular. Comets, on the other hand, have eccentricities close to one. For example, the comet Galea has an eccentricity of 0.967.

Regarding the Earth, the Earth’s orbit has a very small eccentricity, only 0.017. However, it is not exactly zero. This implies that the distance between the Earth and the Sun is not constant.

Aphelion and perihelion

The point at which a planet is closest to the Sun is referred to as perihelion. This term comes from the Greek words “peri” meaning near and “helios” meaning Sun. Conversely, the point farthest from the Sun is called aphelion. In other words, this is the point where the planet is at its maximum distance from the Sun.

The Earth reaches perihelion in early January, when it comes closest to the Sun at a distance of 147.1 million kilometers. It reaches aphelion in early July, when it is 152.1 million kilometers away from the Sun. The difference between the two points is approximately 5 million kilometers.

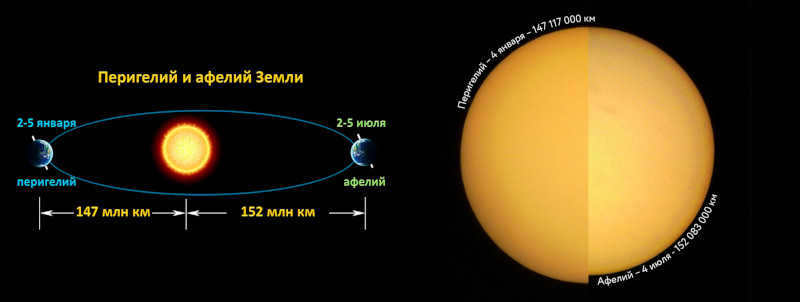
The difference in distance from the sun to the Earth at different times of the year can help explain why winters in the northern hemisphere are milder compared to the southern hemisphere. During winter, the Earth is slightly closer to the sun. Conversely, in July, the Earth receives less solar energy, resulting in cooler summers in the northern hemisphere.

According to Kepler’s first law, we previously mentioned that the Earth follows an elliptical orbit rather than a circular one. In terms of its speed, the Earth’s velocity increases as it gets closer to the Sun and decreases as it moves farther away.

Kepler expressed this concept in the following manner:

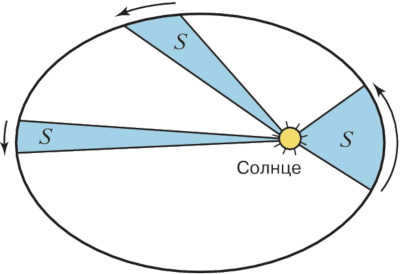
Planets cover equal areas in equal intervals of time.

This is known as the law of areas, which is also referred to as Kepler’s second law. However, it can also be understood as the law of conservation of momentum. What is more intriguing to us is the following equation:

The product of a planet’s linear velocity and radius vector at its perihelion is equal to the product of its velocity and radius vector at its aphelion. This equation represents a specific scenario within Kepler’s second law, specifically for the planet’s maximum and minimum velocity values.

Calculating the Earth’s Maximum and Minimum Velocity

By applying the law of conservation of energy, we can determine the maximum and minimum velocities of the Earth during its motion at perihelion and aphelion.

Moreover, equations for determining the distance from the sun to aphelion and perihelion, using eccentricity and major semiaxis:

Additionally, there is the formula for calculating the initial velocity in space.

Instead of using the distance R in the equation, we substitute it with the semi-major axis a. The semi-major axis of the Earth’s orbit is the average distance from the Earth to the Sun, and this is the value of the semi-major axis we used in the initial calculations. Therefore, the velocity we calculated initially represents the average orbital velocity, which is what we will utilize.

In the law of conservation of energy, we begin by decreasing the mass of the Earth, and also substituting the radius vectors with, correspondingly, .

On careful observation, it can be noted that in the given equations, and , , , represents the square of the average orbital velocity. This value has already been computed in the initial stages. Therefore, it would be convenient to substitute this value here.

By substituting the value of into the first equation, we can simplify the second equation. After performing the necessary transformations, we can express :

Similarly, we can express :

Finally, we can substitute the given values and calculate the result.

The velocity of the Earth around its axis is approximately 30,286.1 meters per second.

meters per second

Kepler’s Third Law

After Kepler published his two laws in 1609, he continued his research and, ten years later, made the discovery of the third law.

The squares of the periods of the planets’ orbits are related to each other as the cubes of the major semi-axes of their orbits.

But that’s a completely different story…

In late July, numerous media sources reported on the phenomenon of the Earth spinning faster, leaving scientists puzzled. By the beginning of August, this topic had made its way to the Russian-speaking corner of the internet. This incident, although without any negative repercussions, highlights the major flaws of modern journalism, not just in the realm of popular science. Here, we will explain how the rotation speed of our planet actually fluctuates, the extent of our knowledge on the causes of these oscillations, and why it is normal for scientists to never have absolute certainty on such matters.

The International Earth Rotation Service (IERS), responsible for monitoring the rotation of the Earth, has reported that June 29th marked the shortest day ever recorded. The deviation from the usual 24-hour period amounted to 1.59 milliseconds. Due to the lengthy process of data analysis, the results were only made known by the end of July. Additionally, it remains uncertain when the causes of this anomaly can be determined with acceptable accuracy. It is likely that this will not occur until next year, although initial reasonable assumptions have already been made. Despite this, the media has managed to sensationalize the situation, exaggerating the circumstances.

Tracing the chronological origins of the chain of emotional publications is not an easy task. The International Earth Rotation and Reference Systems Service (IERS) has not yet released their report on their website, but many publications have received press releases. One of the first portals to publish the relevant news was TimeAndDate. It is important to acknowledge our colleagues for their responsible reporting, as they focused on the main causes of the fluctuations in our planet’s rotation speed without resorting to clickbait. However, the authors of the article couldn’t resist adding a touch of alarmism. Despite the minuscule deviation of June 29 from the “normal” day duration (1.59 milliseconds), they suggested the possibility of adding a “leap second” in the future, which could potentially lead to significant problems with computer systems worldwide.

The speed of the Earth’s rotation has experienced a slight uptick, and if this pattern continues into 2021, we will need to subtract a leap second from the global year on the next New Year’s Day, rather than adding it.

A brief scientific explanation

In order to clarify the physical processes described below, it is important to consider two principles of conservation: momentum and angular momentum (for more detailed and visual explanations, refer to the English-language pages on Wikipedia: 1, 2, respectively). Impulse, which is the product of mass and velocity, serves as a measure of an object’s motion (note: it is a vector quantity). Momentum, also known as angular momentum, is a similar characteristic for rotating objects and their systems. The laws of conservation state that in a closed system, the total sum of all impulses (and angular momenta for rotating objects) remains constant. When two objects collide, their impulses are redistributed, but the overall vector sum remains unchanged.

The law of conservation of momentum can be easily demonstrated with the following scenario: imagine a rocket weighing 100 kilograms (including fuel) that expels 20 kilograms of fuel from its engine at a speed of 1000 meters per second. As a result, the rocket moves in the opposite direction with a speed of 250 meters per second (20 × 1000 = 80 × 250). In real-life applications, a more complex formula (known as Tsiolkovsky’s formula) is required to account for factors such as engine efficiency and changes in the rocket’s mass as fuel is consumed. However, this simplified example effectively illustrates the concept. When two objects collide, the fundamental mechanics remain the same. Putting deformation aside, a 20-kilogram projectile moving at a kilometer per second would have the same effect as the expelled fuel. Upon colliding with a stationary rocket weighing 80 kilograms, the projectile would move in the opposite direction at a speed of 250 meters per second, while the rocket would come to a halt.

A massive layered non-single yula

We will not currently discuss why and in which direction the protoplanetary disk initially rotated. What is important is that the developing Earth gained a small amount of momentum from each grain of sand that fell on it, not to mention larger objects. As a result, it started rotating around its axis, and this speed gradually increased. Once the various natural collisions with celestial bodies came to an end, the rotation speed of our planet should have remained constant.

To put it simply, the Earth cannot maintain a constant angular velocity when considering external influences from other planets and the Sun. This is evident in the fact that the length of the day, known as LOD, increases steadily over long periods of time and fluctuates over shorter periods.

Seismic tomography with high resolution has uncovered variations in the structure of regions at the boundary between the Earth’s core and mantle, resulting in a decrease in seismic wave velocity. The lowest layer of the area under study has been observed.

What factors affect the length of the day?

The duration of the day is influenced by various factors, such as the movement of masses towards or away from the axis of rotation of the planet. Interestingly, heavy precipitation can actually cause the Earth to rotate faster, while active evaporation during hot periods can slow it down. Although one might assume that these processes would balance each other out, this is only true in the long run. On shorter timescales, climatic processes occur at different speeds in different parts of the planet, leading to variations in the manifestation of seasons between the hemispheres. These variations can be attributed to both the tilt of the Earth’s axis and the ellipticity of its orbit around the Sun, which results in an oval trajectory rather than a perfect circle.

There are two primary factors that contribute to the current change in our planet’s rotation rate. As previously mentioned, the Moon exerts a gravitational force on the Earth, causing it to lose angular momentum over time. This process is gradual but ongoing, resulting in a loss of approximately 2.3 milliseconds per century. As a result, 600 million years ago, the length of a day, known as THE LOD, was only 21 hours. Additionally, there is a well-supported hypothesis suggesting that this shorter day length was maintained throughout the entire Precambrian period due to resonance phenomena occurring within the planet’s atmosphere and interior.

During the 19th century, astronomers began to notice the irregularity in the length of the solar day. With the introduction of atomic clocks, scientists were able to measure this irregularity with unprecedented accuracy. The International Earth Rotation Service monitors the actual length of the day and uses statistical analysis to predict whether adjustments need to be made to the clock in the next six months. This is how a leap second, or an extra second, can be added to Coordinated Universal Time (UTC) in order to align it with mean solar time (UT1).

The issue with the extra seconds of coordination is that they cannot be programmed in advance due to the fact that they are added based on current observations of the Earth’s rotation speed. This leads to expensive bureaucracy and implementation in all time-sensitive systems on a global scale. Furthermore, there has never been a removal of seconds, only additions. Predicting the effects of subtracting seconds is not always possible, although theoretically there should be no difficulties. However, no guarantees can be given. This uncertainty surrounding the subtraction of leap seconds is what makes it problematic.

Scientists have discovered that the rotation period of the Earth’s inner core undergoes cyclical changes by analyzing seismograms from nuclear tests conducted in the 1970s.

Instead of a conclusion

The Earth’s rotation rate variability is a well-known and actively researched process that is generally quite understandable. Unfortunately, this issue directly affects the practical aspect of human life: time measurement. Therefore, it is not only of academic interest. In any case, the statement “scientists do not know why the planet is speeding up” is incorrect.

The most probable explanation for the unusual occurrence in June is a phenomenon known as the Chandler wobble. We will delve deeper into this topic during the XIX meeting of the Asia-Oceanic Society for Geosciences (AOGS). As part of the event, a yet unpublished paper will be presented, shedding light on this subject. Interestingly, one of the authors is our fellow countryman, Leonid Zotov.

On the subject

Geologists have put forward a theory that suggests the Earth’s core undergoes changes in its rotational direction

Researchers have discovered which animals have the fastest perception of time

Is there a real connection between cause and effect?

Popular

Scientists specializing in genetics have identified the ancestors of the famous Iceman, Ötzi

A recent study has revealed that Ötzi, the mummified body found in the Alps after thousands of years, was actually bald and had dark skin.

The exchange of cities was a common practice among Bronze Age rulers

Archaeologists in Turkey have made an exciting discovery – a one-of-a-kind tablet with an Akkadian inscription that sheds light on a unique economic situation that occurred nearly four thousand years ago.

Scientists find a breakthrough in transmitting sound through space

A group of physicists from Finland have successfully demonstrated the practicality of “vacuum phonon tunneling”, a phenomenon that allows sound vibrations to traverse through a vacuum gap and transfer from one object to another.

Researchers have discovered a prehistoric creature known as the “ice mouse” that lived during the time of dinosaurs

Scientists have recently unveiled findings about a minuscule animal that inhabited the northern region of Alaska approximately 73 million years ago. What is particularly intriguing about this creature is its ability to thrive in frigid temperatures without entering a state of hibernation. Resembling a shrew, this remarkable species weighed less than an empty aluminum soda can.

An international group of researchers has discovered proof that Vlad Tepes, famously known as Count Dracula, had a rare ailment that resulted in his tears being mixed with blood.

Trading of cities by Bronze Age monarchs

Archaeologists from Turkey have unearthed a one-of-a-kind tablet containing an inscription in Akkadian, which detailed an extraordinary economic circumstance nearly four thousand years ago.

Arms shipment from India to Armenia reveals new export market

Indians have recently started exporting arms to an undisclosed customer, and further analysis has now confirmed that the recipient is Armenia. This marks a significant milestone as it is the first large-scale export of its kind from India, which has not traditionally been known for its military hardware exports.

New study challenges the popular “ten thousand step rule”

For years, it has been widely believed that walking at least ten thousand steps a day is crucial for maintaining good health. However, a new comprehensive study has now debunked this notion, finding that even shorter walks can have significant health benefits. In fact, the study suggests that just four thousand steps a day can reduce the risk of mortality.

Paleontologists have identified what could be the largest creature ever to exist

Ancient remains discovered in South America have been attributed to a prehistoric marine mammal, estimated to have weighed up to 340 tons – surpassing the current record holder, the blue whale, by one and a half times.

Opinions

Could the Moon eventually break away from Earth? There is evidence to suggest that its orbital speed has been gradually decreasing over time, which is also affecting the length of Earth’s day when observed over long periods. In the distant future, the Earth and the Moon may become synchronized, with both bodies completing a rotation on their axes (and the Moon also orbiting the Earth) in approximately 40 current days, if my memory serves me correctly.

It appears as though it would eventually fly away based on intuition. However, in the field of orbital mechanics, intuition rarely proves to be accurate. Perhaps the system will achieve stability. I will need to consult with knowledgeable individuals to obtain further understanding

>Actually, at this stage, you can assign a D grade in physics and not delve into it any further. The Earth’s atmosphere revolves along with the planet, sometimes leading (superrotation), sometimes falling behind due to the prevailing wind directions at a given moment. If the atmosphere were to “stand still,” its surface layer would have eroded all life long ago (the Earth’s rotation has an angular velocity of half a kilometer per second, which is greater than the speed of sound). Continuing to discuss the absence of global warming demonstrates a complete disregard for a vast amount of empirical data (ranging from archaeological to meteorological evidence). Why even write such a statement? Well, honestly, for what purpose? A high school physics curriculum is sufficient to comprehend the inaccuracies in this remark. If it is overlooked, a thirty-minute search on Wikipedia for key concepts is all that is needed.

This individual consistently leaves identical comments on articles that cover similar subjects. Therefore, there is no need for you to expend any effort on engaging with him.))

The Earth’s rotation speed around its axis is gradually decreasing at an extremely slow pace. The gravitational pull between the Earth and the Moon is weakening, but this process is happening at such a negligible rate that it will not have a significant impact anytime soon. Interestingly, this gradual separation between the Earth and the Moon is a result of momentum exchange. The Moon “steals” some of the Earth’s angular momentum, causing an increase in the energy of its orbit and consequently expanding its major semi-axis.

The idea behind angular velocity: the Earth’s rotation on its axis and its orbit around the Sun.

There are two types of motion that our planet undergoes in the vastness of space: rotation around its own axis and rotation around the Sun. In this article, we will delve into the concept of angular velocity and provide you with the essential formulas for calculating this value. Additionally, we will present a detailed calculation of the Earth’s angular velocity as it rotates around its axis and orbits our star.

How fast does an object rotate in terms of angular velocity?

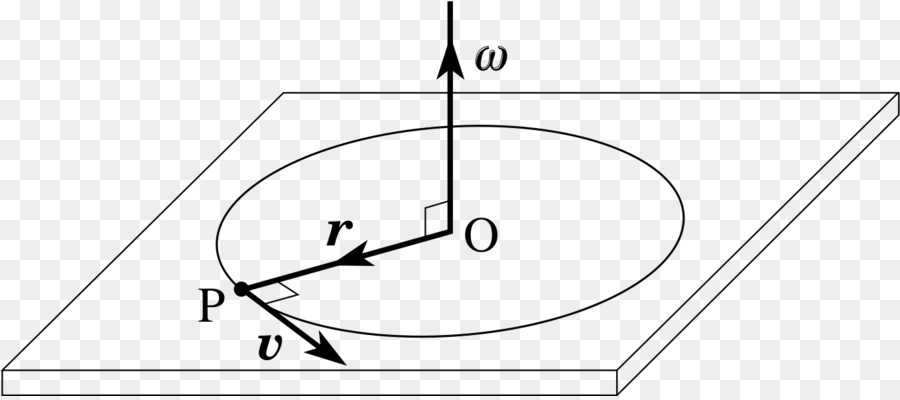
When considering the movement of an object in space over large distances, its dimensions are often ignored. In this case, we introduce the concepts of path and velocity. If we solve the problem of an object’s motion around a certain point or axis of rotation, the distance traveled is always equal to the circumference of the corresponding circle, and the linear velocity is replaced by angular velocity.

Angular velocity is the angle by which an object rotates around an axis per unit time. According to this definition, the unit of measurement for angular velocity is radians per second (rad/s). Degrees per second (˚/s) can also be used. Angular velocity is represented by the Greek letter omega (ω).

Before we move on to the question of what is equivalent to the angular velocity of the Earth’s rotation, it is important to familiarize oneself with the fundamental formulas that describe this value.

As we are aware, the angular measurement of a complete circle is 360 degrees or 2×π radians, where π = 3.1416. If an object completes a full revolution around an axis in a given time period T, the following equation can be derived:

The time period T is referred to as the revolution period, and the value f = 1/T represents the number of revolutions the object will complete per unit of time, thus characterizing its rotation frequency.

Another crucial formula for angular velocity involves the combination of linear velocity and radius of rotation:

If we calculate the unit ω in this equation, we obtain the same value in radians per second (s -1 ). The equation demonstrates that the smaller the distance from the axis of rotation to the body (r), and the greater its linear velocity (v), the larger ω will be.

Using this equation, we can easily calculate the magnitude of v: v = ω×r. Since angular velocity remains constant for a given body, points that are further from the axis of rotation will move at a faster rate.

We utilize these equations and concepts to determine the angular velocity of the Earth’s rotation around its axis and around the Sun.

Revolution of the Earth on its axis

It is common knowledge that our planet undergoes rotation around its axis, with the Earth’s equatorial plane inclined at an angle of 23˚ to the ecliptic plane.

How can we determine the angular velocity of the Earth’s rotation around its axis? We have several formulas to choose from. Given that one complete revolution takes 24 hours, we need to use the formula with the period T to make the calculation. Thus:

In the above equation, the period T is converted into seconds. The resulting value is relatively small.

The calculated value of v, which is equal to ω×r, is 7.27×10 -5 ×6 378 000, resulting in a speed of 463.8 m/s or 1670 km/h.

The speed of the Earth’s rotation is significantly high compared to the speeds we observe in our daily lives. Despite this, humans do not perceive this speed because they are moving together with the air and the ground beneath their feet, allowing them to remain at rest relative to their surroundings.

This rotation of the Earth not only gives rise to the phenomenon of day and night, but also generates the Coriolis force, which affects various processes on Earth, such as altering the direction of winds.

The revolution of our planet around the Sun

Now, we can determine the Earth’s angular velocity as it rotates around the Sun. To do this, let’s utilize the provided data: the precise value of the sideric period of our planet’s orbit is 365 days 6 hours 9 minutes and 9.7632 seconds, which is equivalent to T = 31558149.7632 seconds. Using the formula:

ω = 2×π/T = 2×3.1416/(31558149.7632) = 1.991×10 -7 rad/s.

Therefore, the angular orbital velocity of our planet is 1.5 orders of magnitude lower than the angular velocity of its own axis. Let’s also calculate the linear velocity, taking into account the average radius of the orbit, which is 149,597,871,000 meters:

v = ω×r = 1.991×10 -7 ×149,597,871,000 = 29784.8 m/s = 107,225 km/h.

The existence of the seasons in the Northern and Southern hemispheres is intricately linked to the planet’s orbital motion and the tilt of its axis.

What is the velocity at which the Earth revolves around its axis and the Sun?

Just like any other celestial body, the Earth is in constant motion. Although we may not perceive it, the planet is spinning on its axis and orbiting the Sun at an astonishing velocity. The reason we don’t feel it is similar to being in an airplane or car – we move at the same speed as the vehicle, creating the illusion of stillness.

What is the cause of the Earth’s rotation on its axis?

The Earth’s rotation on its axis, which takes 24 hours to complete, is a crucial factor for the existence of life on our planet. This rotation creates a favorable temperature by allowing for a constant cycle of day and night, which has played a significant role in the evolution of life.

It is important to note that this rotational characteristic is not unique to Earth alone. Every planet in our solar system possesses its own distinct rotation. For instance, the small planet Mercury, located closest to the Sun, completes one rotation in 59 Earth days, while Venus takes an astonishing 243 days to complete a rotation, and interestingly, its rotation is in the opposite direction.

It is common knowledge that the Earth rotates, which may seem like a mundane fact. However, upon closer examination, the underlying reasons for this phenomenon are not entirely clear. To shed light on this matter, we must delve into the formation of the entire solar system.

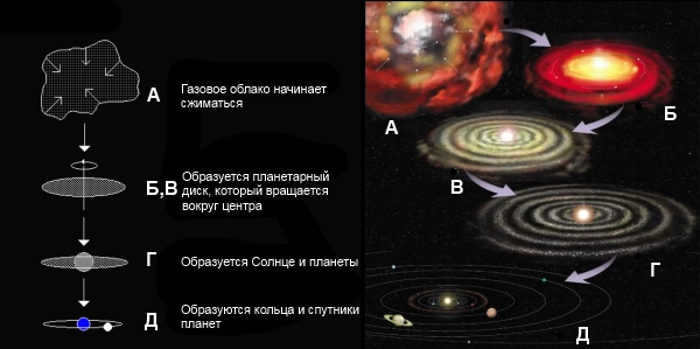
The birth of the solar system

Originally, the solar system was a massive cloud of dust and gas that gradually collapsed into a large disk. This disk then started to spin faster, much like a figure skater extending her arms to increase her speed. In the center, the sun formed, while the planets gathered at a distance. All the celestial bodies within our system lie on the same plane and move in the same direction because they all originated from the same cosmic dust disk.

What is the reason for the Earth rotating faster than other planets?

According to scientists, the Earth’s faster rotation can be attributed to a significant event in its history. It is believed that a massive object, approximately the size of Mars, collided with our planet, resulting in the separation of a large portion that eventually formed the Moon. This collision had the effect of increasing the Earth’s rotational speed in comparison to other planets. However, it is important to note that the gravitational pull of the Moon has a decelerating impact on the Earth’s rotation!

What is the speed of Earth’s rotation on its axis?

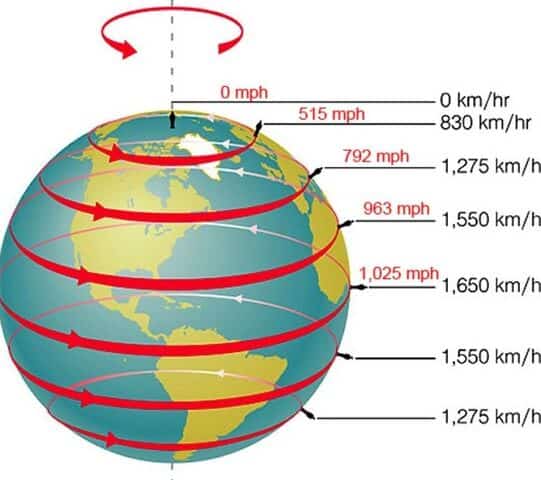
Calculating the speed of Earth’s rotation requires a reference point to be determined. By measuring the rotation relative to the center of the planet, we can determine the speed.

The Earth completes one revolution in 23 hours 56 minutes and 4.09053 seconds, known as the sidereal period. With a circumference of 40,075 kilometers, we can calculate the speed by dividing the circumference by the time, resulting in approximately 1674 km/h or 465 m/s.

Relationship between the Earth’s rotation speed and latitude

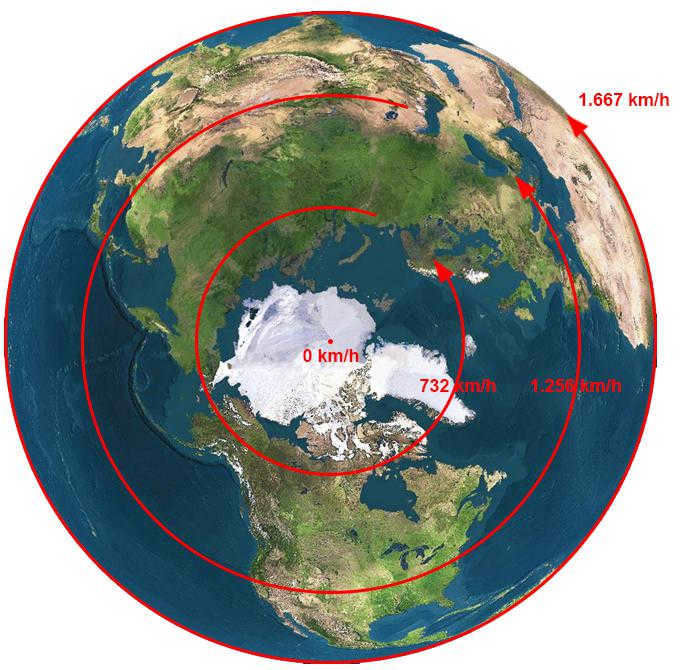
It should be noted that the Earth’s circumference varies depending on the latitude, with the planet becoming narrower towards the poles. As a result, the rotational speed of the Earth differs at different latitudes. The speed decreases as the radius decreases. This means that the rotational speed is almost zero at the North Pole and South Pole.

If you are curious about the rotational speed at different latitudes, you can simply multiply the cosine of the latitude (which can be calculated using a calculator or looked up in a cosine table) by the rotational speed of the Earth at the equator (1674 km/h). For example, the cosine of 45 degrees is equal to 0.7071, so the rotational speed at this latitude would be 1674 x 0.7071 = 1183.7 km/h.

The correlation between the Earth’s rotation speed and latitude

The Earth’s rotation speed at different latitudes

• 10°: 0.9848×1674=1648.6 km/h;
• 20°: 0.9397×1674=1573.1 km/h;
• 30°: 0.866×1674=1449.7 km/h;
• 40°: 0.766×1674=1282.3 km/h;
• 50°: 0.6428×1674=1076.0 km/h;
• 60°: 0.5×1674=837.0 km/h;
• 70°: 0.342×1674=572.5 km/h;
• 80°: 0.1736×1674=290.6 km/h.

Cyclic braking

Researchers have recently observed a connection between seismic activity over the course of a year and the rotational speed of the Earth. While there is no direct correlation between these two phenomena, it is crucial for scientists to uncover any potential clues. This knowledge not only deepens our understanding of the planet, but also has the potential to save countless lives.

Just as many natural processes follow cyclic patterns, the Earth’s rotation itself experiences cycles of deceleration and acceleration, with each cycle lasting five years.

Oscillation of the Earth’s axis

In the field of physics, there are two fundamental concepts that are employed to explain the oscillation of the Earth’s axis – precession and nutation.

Precession refers to the phenomenon in which the momentum of a celestial body undergoes a change in its direction within space. This motion can be likened to that of a spinning top, which initially possesses a vertical axis of rotation but gradually decelerates over time, causing a loss in speed. Consequently, the axis begins to deviate gradually from its customary vertical orientation and starts to trace out a cone-like trajectory. This type of motion is known as precession.

Nutation is a relatively weak movement that resembles a rocking or nodding motion, which is characteristic of a solid object undergoing procession. It is a small wobble of the Earth’s axis that is added to its precessional motion.

The Earth’s Motion Around the Sun

We must not forget that the Earth’s movement consists not only of its own rotation, but also its orbit around the Sun. Our planet is approximately 149,600,000 kilometers away from the star.

Our planet completes a full orbit around the star in 365,256 days, traveling at a speed of 108,000 kilometers per hour or 30 km/sec.

Additional movements

The solar system is not a static object that remains stationary. In reality, while various rotations take place within the system, it is also undergoing rapid movement.

The Sun is situated approximately 26,000 light-years away from the central region of the Milky Way galaxy, which has a width of about 80,000 to 120,000 light-years. Furthermore, it possesses a thickness of 7,000 light years. Our system is positioned on one of the outer arms that is closer to the periphery. It requires approximately 200-250 million years to complete a full revolution around the central region of our galaxy. During this orbital path, the solar system is traveling at a velocity of approximately 250 kilometers per second.

The Milky Way is part of a larger system called the Local Group, which consists of a group of galaxies that are gravitationally bound together. Within this system, the Milky Way is moving at a speed of approximately 300 kilometers per second.

What would happen if the Earth suddenly stopped moving?

There is no chance of suddenly flying out into outer space because gravity keeps us firmly grounded on Earth. However, it’s important to note that gravity is not uniform across the entire planet. Due to the Earth’s spherical shape and rotation on its axis, the planet is slightly flattened at the poles. The equator, which is the widest circle, experiences the highest speed. At the equator, gravity is 0.3% stronger compared to other areas.

NASA declares that halting the planet within the next few billion years is an unattainable feat. However, envisioning a scenario where the Earth comes to an abrupt halt paints a grim picture. If the rotation of the celestial body were to cease, the motion of the atmosphere would persist, resulting in the decimation of everything that once resided on the Earth’s surface due to powerful winds. This would not only affect humans and animals, but also structures, flora, and even the uppermost layers of soil!

The gradual deceleration option, however, represents an actual scenario that our planet will encounter in the distant future. The minimum velocity at which Earth can decelerate is one rotation per 365 days. This circumstance is referred to as “sun synchrony”. In such a scenario, one side will perpetually face the Sun, while the other side, akin to the Moon, will be in perpetual darkness. Nonetheless, as per NASA statements, one can adapt to such a situation.

However, there is no need to worry! The chances of such scenarios happening are practically non-existent!

If you happen to come across an error, please select the text and press Ctrl+Enter.

HOW QUICKLY DOES THE EARTH SPIN?

What is the speed at which the Earth rotates on its axis? It is well known that the change from day to night is caused by the Earth’s rotation. But have you ever wondered how fast it actually spins? And how can we calculate this speed?

When discussing motion in a circular path, there are two types of speeds: angular (ω) and linear (v). Let’s calculate both of these for our magnificent blue planet.

The rotational speed of the Earth

The rotational speed determines how quickly the angle changes over time. As the Earth completes one full rotation, which corresponds to an angle of 360 degrees or 2π radians, within a period of time known as T, the rotational speed can be calculated as:

Just to clarify, this is where the value of 2π comes from.

One radian is the angle subtended by an arc equal to the radius. Thus, to calculate the number of radians in a circle, we divide its circumference, 2πR, by the radius R. The R’s cancel out, resulting in 2π, or approximately 6.28.

We are aware that a day consists of 24 hours, so we can assume that the time it takes for the Earth to complete one rotation around its axis, which we’ll call T, is also 24 hours. However, before we calculate the value of T in seconds and substitute it into the equation mentioned above, let’s consider the fact that the Earth also revolves around the sun. As a result, the period of its rotation around its own axis is slightly shorter than a solar day and amounts to 23 hours, 56 minutes, and 4 seconds. This is commonly referred to as a stellar day. In terms of seconds, we can express it as T=86164 s.

Now, let’s determine the angular velocity:

The speed of the Earth’s rotation

When it comes to the angular velocity of the Earth’s rotation, it remains the same for any location on our planet. Whether you’re in Antarctica, Africa, or at home, everyone experiences the same angular velocity. However, the linear velocity is a different story. At the equator, the linear velocity is at its maximum, and it gradually decreases as you move towards the poles. This is because it is directly influenced by the radius of the rotation circle. So, if you were to climb onto a stool to change a light bulb, your linear velocity would increase. Keep in mind that linear velocity doesn’t describe the rotation of the Earth as a whole, but rather the rotation of specific points on its surface.

Given that the angular velocity is ω, we can confidently express:

The equatorial radius of the earth is R = 6378245 m, so the linear velocity at that location will be equivalent to: m/s.
By way of comparison, the speed of sound in air is 365 m/s. This implies that while sitting calmly in a chair in Africa or Indonesia, our movement surpasses the speed of sound. When converted to kilometers per hour, that equates to 1674 kilometers per hour. In general, this is comparable to the speeds of supersonic aviation.

Linear velocity at different latitudes

However, this calculation is only accurate at the equator. As you move closer to the poles, the linear velocity will decrease due to the decreasing radius of rotation.

To determine the radius of rotation at a specific latitude, you can multiply the cosine of that latitude by the Earth’s radius.

For example, in St. Petersburg, which is located at a latitude of sixty degrees north, the cosine of sixty degrees is one second. This means that the radius of rotation will be half of the Earth’s radius, resulting in a linear speed that is also half of the equatorial speed, or 837 km/h.

Now it’s your turn. What is the linear speed at your current location? Feel free to share your answers in the comments, and I’ll bid you farewell. Take care and see you soon!

The idea of angular speed: the Earth’s turning on its axis and orbiting around the Sun

There are two types of motion that define the movement of our planet in the vastness of space: rotation around its own axis and rotation around the Sun. In this article, we will explore the concept of angular velocity, provide the necessary formulas for calculating this value, and present a calculation of the Earth’s angular velocity as it rotates around its axis and orbits our star.

When considering the motion of an object in space over long distances, typically its size is disregarded. In this scenario, the notions of path and velocity are introduced. If we are solving for the motion of an object around a certain point or axis of rotation, then the distance traveled will always be equal to the circumference of the corresponding circle, and the linear velocity is replaced with angular velocity.

Angular velocity represents the angle by which an object rotates around its axis in a given unit of time. Based on this definition, the unit of measurement for angular velocity is radians per second (rad/s). Degrees per second (˚/s) can also be used. Angular velocity is denoted by the Greek letter omega ω.

Primary equations

Prior to delving into the inquiry of what is the angular velocity of the Earth’s rotation equivalent to, it is essential to acquaint oneself with the primary equations that depict this quantity.

As it is widely recognized, the angular measurement of the complete circle amounts to 360 ˚ or 2×π radians, where π = 3.1416. In the event that an object completes a full revolution around an axis within a time interval of T, the ensuing equation can be formulated:

The time interval T is referred to as the period of revolution, and the value f = 1/T indicates the number of revolutions the object will undertake within a unit of time, thus characterizing the frequency of its rotation.

Yet another pivotal equation pertaining to angular velocity is the expression that combines linear velocity and radius of rotation:

If we examine the unit ω in this expression, we obtain the same radians per second (s -1 ). The equation demonstrates that the smaller the distance from the axis of rotation to the body (r), and the greater its linear velocity (v), the larger ω will be.

With this equation, we can easily express the magnitude of v: v = ω×r. Since angular velocity remains constant for a given body, points farther from the axis of rotation will move at a faster rate.

We utilize these formulas and principles to determine the angular velocity of the Earth’s rotation around its axis and around the Sun.

The rotation of the Earth on its axis

It is common knowledge that the Earth revolves around its axis, with the equatorial plane inclined at a 23˚ angle to the ecliptic plane.

How can we determine the angular velocity of the Earth’s rotation around its axis? We can use any of the formulas provided above. Since we know that one revolution takes 24 hours, we can use the formula with the period T to calculate it. The calculation is as follows:

Here, the value of the period T is converted into seconds. The resulting value is quite small.

It is interesting to calculate the linear velocity at which points on the Earth’s surface at latitude 0˚ (the equator) are moving. The equatorial radius of the Earth is 6,378,000 meters. By substituting this value into the velocity formula, we can determine the result:

The velocity is equal to the angular velocity times the radius, which is equal to 7.27 times 10 to the power of -5 times 6,378,000, resulting in a velocity of 463.8 meters per second or 1,670 kilometers per hour.

The speed at which the Earth rotates on its axis is quite significant when compared to the speeds we experience in our daily lives. However, humans do not perceive this speed because we are moving along with the air and the ground beneath our feet, effectively remaining at rest relative to them.

This rotation of the Earth not only gives rise to the phenomenon of day and night, but also leads to the emergence of the Coriolis force, which affects various processes on Earth. One example of this is how the Coriolis force influences the direction of winds.

Now we will compute the Earth’s rotational angular velocity around the Sun. For this calculation, we will use the given data: the precise value of the sideric period of our planet’s orbit is 365 days 6 hours 9 minutes and 9.7632 seconds, which can be represented as T = 31558149.7632 seconds. Using the formula:

ω = 2×π/T = 2×3.1416/(31558149.7632) = 1.991×10 -7 rad/s.

Therefore, the angular orbital velocity of our planet is 1.991×10 -7 rad/s, which is 1.5 orders of magnitude less than the angular velocity of its own rotation. Let’s now calculate the linear velocity, knowing that the average radius of the orbit is 149,597,871,000 meters:

v = ω×r = 1.991×10 -7 ×149,597,871,000 = 29784.8 m/s = 107,225 km/h.

With this incredible speed, our planet moves through outer space around the Sun.

The connection between the existence of seasons in the Northern and Southern hemispheres is linked to the planet’s orbital motion and the tilt of its axis.

Earth’s vector of angular velocity

The rate of rotation of the Earth

As we are aware, our planet is in motion, not just around the Sun, but also around its axis. Moreover, we understand that any movement is characterized by a specific velocity, which can depend on various factors, similar to the movement itself. Consequently, the Earth’s rotation also possesses its own velocity.

Planet Earth

Velocity is a vector physical quantity that describes the speed of movement of a material point over a given time interval relative to the magnitude of the interval.

The rotational velocity of the Earth

Indeed, the velocity of the Earth is a relative concept, as it depends on the chosen reference point. In order to calculate the speed at which the Earth rotates around its axis, the center of the planet is taken as the reference point.

However, when discussing this parameter of the Earth’s rotation, it is important to note that velocity can be divided into angular and linear components.

Angular velocity

Angular velocity refers to a measurement that calculates the rate of change of an angle over a specific period of time. It can be thought of as the speed at which an object’s angle changes over time. Angular velocity is typically measured in radians per second and remains constant for all points.

To put it in perspective, it takes approximately 23 hours, 56 minutes, and 4.09053 seconds for our planet to complete one full rotation around its axis. This is known as a sidereal day.

The formula for calculating angular velocity is the ratio of the change in angle to the corresponding time period.

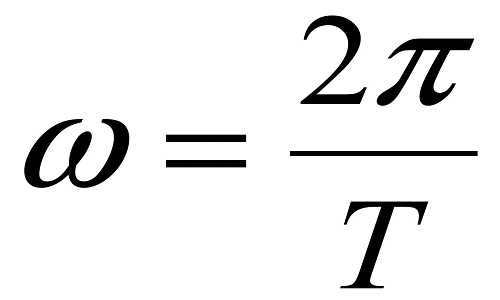
Formula for angular velocity

Given that the Earth completes a full revolution of 360 degrees or 2π (2*3.14=6.28) in a time of 86344 seconds, the angular velocity of the Earth’s rotation around its axis is approximately 7.26851851851-5s-1.

Velocity in a Straight Line

This property is utilized to represent the speed of movement along a circular path. As we are aware, when an object rotates in a circle, its various points have varying velocities. Nevertheless, the angular size of displacement for these points remains constant.

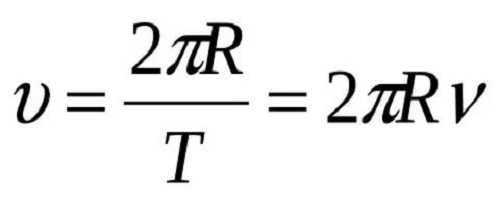
The equation for linear velocity

This implies that the Earth’s rotational speed is approximately 465 m/s. In other words, this calculation is obtained by dividing the circumference by the time it takes to complete one revolution.

However, the Earth’s speed varies due to the changing circumference at different latitudes. This is because the radius of the planet decreases towards the poles. As a result, different latitudes have different rates of rotation. In simpler terms, regions with a smaller radius have a slower speed. For instance, the speed is almost zero at the poles and 1674 km/hr at the equator.

To determine the rotational velocity of the Earth at a different latitude, one must multiply the cosine of the desired latitude by the equatorial velocity. For instance, if we wish to calculate the speed of the planet at a latitude of 30 degrees, we would multiply the cosine of 30 degrees (which is 0.866) by 1674. This would yield a result of 1449.7 km/hour.

The Velocity of Earth’s Movement Relative to the Sun

As the Earth orbits around the Sun, it maintains a specific velocity.

It takes approximately 365 days, 5 hours, 48 minutes, and 46 seconds for the Earth to complete one full revolution around the Sun. This period is commonly known as a year. Interestingly, each year accumulates an extra 5 hours. To account for this, every fourth year, an additional day is added to the calendar. These years are known as leap years.

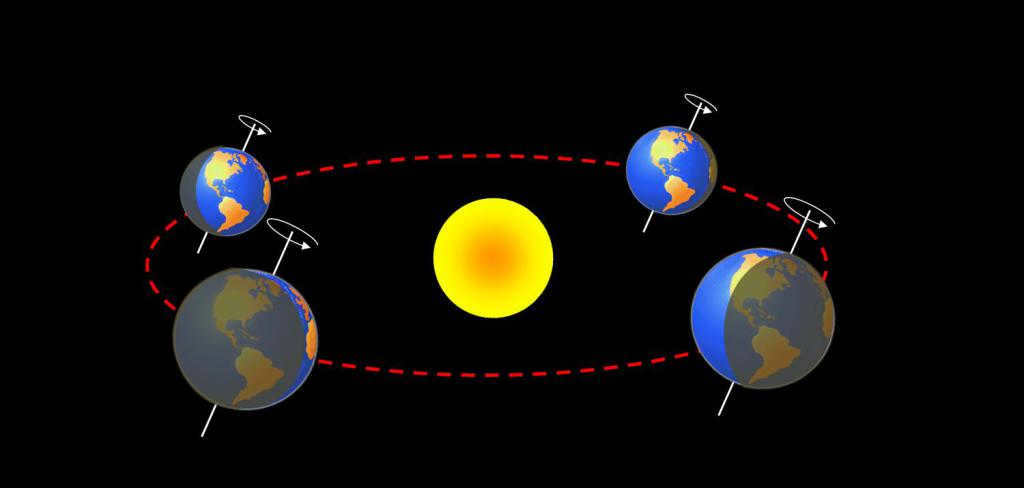
The Earth’s orbital motion around the Sun

By analyzing the available data on the duration of the Earth’s complete revolution around the Sun, it is possible to easily calculate the velocity at which it moves in relation to the Sun. It is important to note that we are observing the Earth’s orbit. Therefore, we can determine the precise speed at which the Earth travels along its orbital path.

How to determine the Earth’s velocity in its orbit around the Sun

In order to calculate the rate at which the Earth moves around the Sun, you need to multiply the radius of the orbit or the distance to the Sun (approximately 150 million km) by 2π (2 times 3.14 equals 6.28), giving us a total of 942 million kilometers. We then divide this by the duration of the interval, which is 31,536,000 seconds (365 days times 24 hours times 3600 seconds). The result is a velocity of 29.87 kilometers per second.

The accepted average speed of the Earth in its orbit around the Sun is 30 km/sec.

Scientists have observed that the Earth’s rotational speed is gradually decreasing, with periodic cycles of acceleration or deceleration lasting five years. However, the exact cause of these changes remains unknown. Thus, continuous observation and monitoring of our planet’s movement is necessary in hopes of uncovering a connection behind this phenomenon.

The idea of angular speed: the Earth’s rotation around its own axis and its orbit around the Sun

There are two types of rotation that define the movement of our planet in space: rotation around its own axis and rotation around the Sun. This article explores the idea of angular velocity, presents the formulas needed to calculate this quantity, and provides calculations for the angular velocity of the Earth’s rotation on its axis and around the Sun.

What is the rotational angular velocity?

When considering the motion of an object in space over long distances, its size is often disregarded. In such cases, we introduce the concepts of the object’s path and velocity. When solving the problem of an object moving around a point or axis of rotation, the distance traveled is always equal to the circumference of the corresponding circle, and the linear velocity is replaced by angular velocity.

Angular velocity is the angle by which an object rotates around its axis per unit of time. This quantity is measured in radians per second (rad/s) or degrees per second (˚/s). It is commonly represented by the Greek letter omega (ω).

Before we discuss the question of what is equal to the angular velocity of the Earth’s rotation, it is important to understand the basic formulas that describe this value.

As we know, the angular measure of a complete circle is 360 degrees or 2×π radians, where π is approximately equal to 3.1416. If an object completes a full revolution around an axis in time T, we can express this as:

The time T is known as the period of revolution, and the value f = 1/T represents the number of revolutions the object will make per unit time, which is also known as its rotational frequency.

Another important formula for angular velocity combines linear velocity and the radius of rotation:

If we examine the unit ω in this expression, we obtain the same radians per second (s -1 ). The equation demonstrates that as the distance from the axis of rotation to the object (r) decreases and its linear velocity (v) increases, ω will also increase.

Using this equation, we can easily calculate the magnitude of v: v = ω×r. Since angular velocity remains constant for a given object, points further from the axis of rotation will move at a faster rate.

We apply these formulas and principles to determine the angular velocity of the Earth’s rotation around its axis and around the Sun.

The axial rotation of Earth

It is common knowledge that our planet undergoes rotation around its axis, with the Earth’s equatorial plane inclined at an angle of 23˚ to the ecliptic plane.

How can we determine the angular velocity of the Earth’s rotation around its axis? We have the freedom to utilize any of the formulas provided above. Given that one complete revolution takes 24 hours, we can employ the formula that involves the period T to calculate it. The equation becomes:

Here, the value of the period T is converted into seconds. The resulting value is relatively small.

The velocity is equal to the angular velocity multiplied by the radius, which can be calculated as 7.27 × 10 -5 × 6,378,000. This gives us a velocity of 463.8 m/s, which is equivalent to 1,670 km/h.

The measured value is significantly large when compared to the speeds that are observable in daily life. This rapid rotation of the Earth is not directly felt by humans as they are moving along with the air and the ground beneath their feet at the same speed, thus remaining at a relative state of rest.

This rotation of the Earth not only gives rise to the phenomenon of day and night, but also results in the emergence of a force known as the Coriolis force. This force influences various Earth processes, such as altering the direction of winds.

The Earth’s rotation in its orbit

Now we can determine the Earth’s angular velocity as it rotates around the Sun. To do this, we will use the given data: the sideric period of the Earth’s orbit is precisely 365 days 6 hours 9 minutes and 9.7632 seconds, which can be represented as T = 31558149.7632 seconds. Using the formula:

ω = 2×π/T = 2×3.1416/(31558149.7632) = 1.991×10 -7 rad/s.

Therefore, the angular orbital velocity of the Earth is 1.5 orders of magnitude smaller than its rotational velocity around its own axis. Let’s also calculate the linear velocity, taking into account that the average radius of the Earth’s orbit is 149,597,871,000 meters:

v = ω×r = 1.991×10 -7 ×149,597,871,000 = 29784.8 m/s = 107,225 km/h.

The existence of the seasons in the Northern and Southern hemispheres is determined by the orbital motion of the planet and the tilt of its axis.

I. Mechanics

Online Test

Due to the uniform change in direction of linear velocity, motion on a circle cannot be considered uniform, but rather equidecelerated.

Angular speed

Let’s choose a point on the circle 1. We will draw a radius. In a certain amount of time, the point will move to point 2. At the same time, the radius will cover a certain angle. The angular speed is equal to the numerical value of the angle covered by the radius per unit of time.

Period and frequency

The period of rotation T is the time it takes for a body to complete one full revolution.

The frequency of rotation is the number of revolutions per second.

The frequency and period are related by the following equation:

Relationship to angular velocity

Linear velocity

Linear velocity is the velocity at which every point on a circle moves. The linear velocity vector always aligns with the tangent to the circle. For instance, the sparks produced by a sharpener move in the same direction as the instantaneous velocity.

Let’s take a point on the circle that completes one revolution in a period of T. The distance covered by this point is equal to the circumference of the circle.

Centripetal acceleration

When an object moves in a circular path, the acceleration vector is always perpendicular to the velocity vector and directed towards the center of the circle.

By using the aforementioned formulas, we can establish the following relationships:

Points that lie on a straight line extending from the center of the circle (such as points on the spokes of a wheel) will have the same angular velocity, period, and frequency. This means that they will rotate in the same manner, but with different linear velocities. The farther the point is from the center, the faster it will move.

The law of velocity addition also holds for rotational motion. If the motion of an object or a frame of reference is non-uniform, the law applies to the instantaneous velocities. For instance, the velocity of an individual walking along the periphery of a rotating carousel is equivalent to the vector sum of the linear velocity due to the carousel’s rotation and the person’s velocity.

The Earth is involved in two primary rotational movements: diurnal (around its axis) and orbital (around the Sun). The Earth takes approximately 1 year or 365 days to complete one orbit around the Sun. It rotates on its axis from west to east, completing one rotation in approximately 1 day or 24 hours. Latitude is defined as the angle between the equator’s plane and the direction from the Earth’s center to a specific point on its surface.

Connection to Newton’s second law

In accordance with Newton’s second law, force is the cause of any acceleration. When a moving object experiences centripetal acceleration, the types of forces that bring about this acceleration can vary. For instance, if an object moves in a circular path while attached to a rope, the force at play is the force of elasticity.

Alternatively, if an object is at rest on a rotating disk and moves with the disk around its axis, the force involved is the force of friction. If this force is removed, the object will then continue to move in a straight line.

Deriving the Formula for Centripetal Acceleration

Let’s examine the motion of a point on a circle as it moves from point A to point B. The linear velocity at point A is represented by vA and at point B by vB. Acceleration can be defined as the change in velocity per unit time. Now, let’s calculate the difference between these two vectors.

The difference between the vectors can be expressed as . By simplifying this equation, we can obtain the formula for centripetal acceleration.

Cycloidal motion*

The point on the wheel rotates uniformly in a circle of radius R with a velocity that only changes in direction. The centripetal acceleration of the point is directed towards the center of the circle along the radius.

Now, let’s consider a stationary reference frame associated with the Earth. The total acceleration of point A remains the same in magnitude and direction, as acceleration doesn’t change when transitioning between inertial reference frames. From the perspective of a stationary observer, the trajectory of point A is no longer a circle, but a more complex curve known as a cycloid, along which the point moves unevenly.

The instantaneous velocity can be calculated using the formula

What is the speed at which the Earth rotates around its axis? It is common knowledge that the rotation of the Earth is responsible for the transition between day and night. However, have you ever pondered the speed at which it rotates? And how can we calculate this speed?

When discussing uniform motion on a circular path, there are two types of speeds: angular (ω) and linear (v). Let’s determine both for our magnificent planet.

The Earth’s rotation speed: understanding angular velocity

Angular velocity refers to the rate at which an angle changes over time. In the case of Earth’s rotation, one complete revolution corresponds to a 360-degree angle or 2π radians. The time taken for this revolution is known as the period T. Consequently, the angular velocity can be expressed as:

Just to clarify, the value of 2π is derived from the fact that one radian represents an angle with an arc equal to the radius. To determine the number of radians in a full circle, we divide its circumference (2πR) by its radius R. The radius terms cancel out, leaving us with 2π. This value is approximately equal to 6.28.

We are aware that a day consists of 24 hours, and therefore we can infer that the duration of Earth’s rotation around its axis, T, is also 24 hours. However, let’s not rush into converting this time into seconds and plugging it into the equation mentioned above. Due to the fact that the Earth also orbits around the sun, its rotational period around its axis is slightly shorter than a standard solar day, measuring at 23 hours, 56 minutes, and 4 seconds. This is commonly referred to as a stellar day. In terms of seconds, this equals T=86164 s.

Now, let’s proceed to calculate the angular velocity:

The Earth’s rotation and its linear velocity

When considering the angular velocity of the Earth’s rotation, it remains constant regardless of the location on our planet. Whether you are a penguin in Antarctica, an elephant in Africa, or simply at home, the angular velocity remains the same for everyone. However, the linear velocity is a different story. The linear velocity is highest at the equator and decreases as you move towards the poles, as it is directly influenced by the radius of the Earth’s rotation. For instance, if you were to climb on a stool to change a light bulb, your linear velocity would increase. It is important to note that the linear velocity does not describe the Earth’s rotation as a whole, but rather the rotation of specific points on its surface.

Given that the angular velocity is , we can confidently state:

The equatorial radius of the earth is R = 6378245 m, thus resulting in a linear velocity of: m/s.
For reference, the speed of sound in air is 365 m/s. This implies that while sitting calmly on a chair in Africa or Indonesia, our movement surpasses the speed of sound. If we convert that to kilometers per hour, it is 1674 kilometers per hour. In general, our speeds are comparable to those of supersonic aircraft.