Now, let’s shift our focus to the historical development of the theory of gravitation. Setting aside the inquiry into the essence of gravitation, it is worth mentioning that, from a “utilitarian” perspective (in order to compute the motions of celestial bodies), it was crucial to understand the relationship between the force of gravitational interaction and the distance separating these entities.
During the year 1684, Edmund Halley, an astronomer and physicist from England who held the title of Astronomer Royal, arrived at the conclusion that the force of gravity diminishes as the square of the distance. This hypothesis appeared to be reasonable. It is logical to assume that if an influence spreads outward symmetrically from a central source, the area affected by this influence will increase in proportion to the square of the distance. As a result, it is probable that the strength of this force will decrease in relation to this expanding area, meaning that it will be inversely proportional to the square of the distance. However, Halley and his colleagues were unable to mathematically prove that this law of attraction would result in the planets moving in elliptical orbits.
The encounter with Halley rekindled Newton’s fascination with the intricacies of gravitation and planetary motion. Let’s revisit the tale of the descending apple and delve into its intricacies. If the event itself did not actually occur, it is inevitable that such a legend would emerge. In essence, the question arises: does the very same force that holds the Moon in its celestial path around the Earth also govern the apple’s descent? This folklore represents a paradigm shift in scientific comprehension of gravity, bridging the mundane concept of gravity that we witness on a daily basis with the profound one that governs the movement of celestial bodies and the entire cosmos.
Newton discovered that the acceleration of a body moving uniformly on a circle is caused by a constant force directed towards the center of the circle. This acceleration is known as centripetal acceleration and can be calculated using the formula acc = v 2 /R. Kepler’s Third Law, on the other hand, describes the relationship between the periods of revolution of the planets around the Sun and their distances from it. By applying this relationship to circular motion, Newton was able to determine the velocity of linear motion, which is approximately equal to 1/R 1/2.
Newton’s achievements as a physicist would not have been possible without his development of the necessary mathematical tools, as we have previously discussed. This actually marked the birth of an entirely new branch of mathematics – mathematical analysis. Using this new field, Newton demonstrated that the elliptical shape of orbits is a result of motion under the influence of a force directed towards one of the foci of the ellipse, with the magnitude of the force being inversely proportional to the square of the distance from it. However, it was only in 1685, with the aid of the mathematical analysis apparatus he had created, that Newton was able to prove that the gravitational attraction of the Earth could be treated as if its entire mass were concentrated at its center. This discovery was groundbreaking, as it provided Newton with the justification for the previously employed method of comparing the accelerations of the moon and an apple.
Newton’s laws of mechanics provided conclusive proof that there is no distinction between bodies that attract and bodies that are attracted. All bodies that gravitate mutually attract, thus the laws of gravity hold true universally.
Let’s summarize his conclusion briefly. In close proximity to the Earth’s surface, all objects experience the same acceleration, denoted as g, regardless of their mass. Additionally, the force acting on an object on the Earth’s surface is directly proportional to its mass, resulting in the equation F = mg. Furthermore, as stated by the third law of mechanics, if a force is exerted on a body with mass m from another body with mass M, the body with mass m exerts an equal but opposite force on the body with mass M. For example, not only does the Earth attract the Moon, but the Moon also attracts the Earth. Consequently, the force of mutual attraction between the two bodies must be proportional to the mass of each body. It has already been established that this force is inversely proportional to the square of the distance between the bodies. Therefore, the force of mutual attraction between the masses m and M at a distance r from each other can be defined by the following expression:
The law of universal gravitation can be defined as the formulation of the law of universal gravitation, where the coefficient of proportionality known as the universal gravitational constant, denoted as G, plays a crucial role. The value of G signifies the strength of the gravitational interaction and is considered one of the fundamental constants in the world. These constants, including G, determine the behavior of the Universe as a whole and its individual components.
There is no rational basis for equating these two types of mass. In fact, gravitational mass can be thought of as the gravitational equivalent of electric charge. It is possible for two objects with the same inert mass to possess vastly different electric charges, resulting in differing accelerations when subjected to the same electric field. On the other hand, in the gravitational field of the Earth, objects with varying inert masses consistently fall at the same rate of acceleration. This can only occur if the ratio of gravitational mass to inert mass remains constant for all objects.
Newton performed a series of experiments in order to determine if this ratio differed for various objects. No such variation was found, and this remains true to the present day. Because these two types of mass are always in the same proportion to each other, the unit of measurement for them was selected so that their ratio would be equal to one. This is reflected in the fact that the equation for the gravitational force on Earth’s surface takes the form of a second law: F = mg.
The fact that inertial and gravitational masses are equal is referred to as the equivalence principle. Later on, we will see how this principle plays a crucial role in Einstein’s general theory of relativity.
The significance of the law of universal gravitation cannot be overstated. Newton demonstrated that an object follows a path of conic section (such as a circle, ellipse, parabola, or hyperbola) when a force that is inversely proportional to the square of the distance and directed towards the focus of the curve acts upon it. Conversely, the movement of an object under the influence of such a force adheres to Kepler’s laws. Newton also illustrated that the effects of this universal force can account for the movements of the moon and planets, the acceleration of falling objects, the behavior of Jupiter’s moons, and the occurrence of ocean tides.
Additional phenomena were also elucidated and foreseen. Newton made a prediction that, due to its rotational motion, the Earth should exhibit a slight bulge near the equator and a flattening at the poles. He expounded on how this departure from a perfect spherical shape leads to a phenomenon known as precession, which was first observed by Hipparchus nearly two millennia ago. Precession, the gradual rotation of the Earth’s axis, causes the celestial pole to trace a circular path in the sky. If the Earth were a perfect sphere, this occurrence would not be observable. However, as a result of the equatorial bulge and the axial tilt, the gravitational forces exerted on the Earth by the Sun and Moon cause the axis to undergo a rotational motion, tracing out a conical surface. Analogously, just as the axis of a spinning top rotates when it is tilted away from the vertical, the external force causing precession in this case is the gravitational force exerted by the Earth.
By analyzing observational data of comets and using Newton’s laws, Halley was able to determine that some of these observations were related to the same comet. He then made a prediction about when this comet would appear again, and when it actually did, it was named after him. Known as Halley’s Comet, it is the only short-period comet (with an orbital period of approximately 76 years) that can be seen with the naked eye. The last time it was visible near the Sun and Earth, based on Newton’s calculations, was in March 1986. During this time, Halley’s Comet was observed not only by amateur astronomers and professional scientists, but also by five international spacecraft.
By uncovering the law of universal gravitation, scientists were able to explore how planets affect one another through their mutual attraction. Consequently, by analyzing the disruptions in Uranus’s movement, they could accurately compute the trajectory of an unidentified planet situated beyond Uranus that was responsible for these disturbances. Eventually, this planet was found exactly where predicted and was designated as Neptune.
In 1803, William Herschel, an English astronomer and optician (1738-1822), published his observations indicating that many stars, previously seen as individual dots, were actually double stars, consisting of a pair of stars orbiting each other under the influence of mutual gravity. These systems came to be known as double stars. Further research confirmed that the motion of double stars followed Kepler’s laws and Newton’s law of universal gravitation. In 1842, Friedrich Bessel, a renowned German astronomer (1784-1846), used Newton’s law to predict the existence of an invisible satellite around the star Sirius. This satellite was eventually discovered ten years later!
By the mid-19th century, it was widely accepted that Newton’s law of universal gravitation applied universally throughout the observable universe.
This text serves as an introductory fragment.
Further Reading
2. Newton’s Laws and the Dynamics of a Material Point
2. Newton’s Laws and the Dynamics of a Material Point In classical mechanics, the study of the laws of motion starts with the simplest scenario: the study of how a material point moves in space and time.
The concept behind this project is simple – to move without any support in empty space. In our initial physics classes, we are introduced to the law of “action and reaction” or “Newton’s third law”: the force exerted on an object is met with an equal and opposite force.
A Critique of Newton’s Mechanics and Euclid’s Geometry
The theory of electrons and the electrodynamics of moving media have led to radical conclusions, including the rejection of the notion of unchanging solid particles. In nature, there are no fixed bodies or unchanging particles; the shape and size of objects are not constant.
Newton’s Mechanics
The theory of gravitation developed by Sir Isaac Newton would not have been possible without the application of his laws of mechanics. While we will not delve into the specific details that can be found in any high school physics textbook, let us present these three fundamental laws in their definitive formulation. It is unquestionable that these laws serve as the foundation for Newton’s entire body of work.
Newton’s theory of gravitation, known as the Corpuscular Theory of Gravitation, was gaining an increasing number of supporters. The law of inverse squares, which stated that the force of gravity between two objects is inversely proportional to the square of the distance between them, was widely accepted and few doubted its validity. However, there were still debates and discussions about the nature of gravity itself and how it is transmitted between objects. Many scientists speculated that gravity is transmitted through the interaction of particles.
Chapter 4: Transition from Newton’s Mechanics to Maxwell’s Electrodynamics
In Chapter 4 of my book, titled “From Newton’s Mechanics to Maxwell’s Electrodynamics,” I did not encounter much difficulty in deciding where to begin. It was clear to me that I should start with the simplest and most understandable concepts. This approach is similar to the one advocated by René Descartes in his famous work “Discourse on Method.” Now, let us delve into the subject matter further.
Horzhava’s theory of gravity
Horzhava’s theory of gravitation is a prominent vector-tensor theory of gravitation and is currently considered one of the most widely recognized theories in the field. It was first introduced in 2009 by an esteemed American string theorist hailing from the Czech Republic.
Newton’s Law
After being discussed in the third reading, the law of universal gravitation proposed by Newton underwent revision. Folklore Testing Newton’s Law is an essential part of understanding the concept of gravity. Making sense of Newton’s law is crucial for comprehending ideas related to gravity in a broader context. One might wonder how to apply it effectively.
Systems of the world (from ancient times to Newton)
The study of systems of the world, from ancient times to Newton, is a testament to the nature of science. Science, by its very definition, rejects the idea of fetishes and is unafraid to challenge outdated beliefs. It values the wisdom gained from experience and practice. Without this approach, science as we know it would not exist.
One of Newton’s remarkable scientific accomplishments is his daring proposition that every physical object possesses an essential property, aside from its evident characteristics like hardness, elasticity, and weight:
The Revolutionary Impact of Newton’s Laws
Furthering his research on objects influenced by gravitational forces, Newton resolved the problem entirely in 1679. Initially, his intuitive hypotheses from 1666 were not fully developed due to his incomplete understanding at the time.

What is the concept of universal gravitation?
The planet Earth functions as a massive magnet, exerting an attractive force on objects in its vicinity, whether it be a pencil slipping from one’s grasp or an asteroid passing by. Throughout the course of scientific progress, numerous scholars have offered their interpretations and definitions of the universal gravitation phenomenon. However, it wasn’t until 1687, with the publication of Isaac Newton’s groundbreaking treatise “Mathematical Principles of Natural Philosophy,” that the existence and influence of universal gravitation were officially proven.

Did you know? A copy of the famous book “Principia Mathematica” was recently sold at an auction for a staggering price of 3.7 million dollars.
Building upon Johannes Kepler’s empirical laws that described the heliocentric model of our solar system, Sir Isaac Newton formulated a groundbreaking law that explains how all objects are mutually attracted to each other.
Furthermore, the strength of interaction increases as the mass increases, and is inversely proportional to the square of the distance between objects:
Even though this phenomenon is hardly noticeable for objects with relatively small mass, gravity is the force that governs the movement of celestial bodies. The formulation of this law helps us understand why planets revolve around the Sun and why the Moon orbits the Earth.
The origin of the force of universal gravitation
While the significance of gravity in the functioning of the universe is evident and indisputable, the source of this force remains a complex and elusive question. In the early 20th century, Albert Einstein introduced the special and general theories of relativity, offering his unique perspective on the nature of universal gravitation. According to Einstein, space and time form a unified fabric known as the space-time continuum, encompassing four dimensions, with time being one of them. However, since humans perceive space and the flow of time separately, they can only observe a two-dimensional representation of this continuum. Einstein proposed that gravity arises from the presence of massive objects, which deform space by projecting the four-dimensional continuum onto it.

To enhance the clarity of the scientist’s concept, we can use the example of two balls with different masses and a regular sheet of paper. Let’s imagine that the sheet of paper is held horizontally by its edges, and we place one of the heavier balls in the center. As expected, the paper will bend due to the weight. Now, if we roll a lighter ball in a straight line on the paper’s surface, we will observe that its trajectory forms an arc, curving towards the first, heavier ball. Interestingly, from the perspective of the lighter ball, its motion remains straight. This simple demonstration provides us with a simplified representation of the emergence of gravity as a phenomenon.
Legend has it that while walking in the garden and observing the moon, Newton witnessed the descent of an apple to the ground (in an alternate version, the apple landed on the scientist’s head). In that very moment, he pondered the potential of a similar force that kept the satellite suspended in the sky and caused the fruit to plummet from tree branches. This speculation marked the commencement of his investigation into the law of gravity.

Historians today have doubts about this myth, which is understandable. However, the main historical fact remains that Newton was the first scientist to recognize that both bodies on Earth and in space are influenced by the same force. Prior to this realization, people had categorized gravity into two different types: the first type was responsible for the imperfect interactions on Earth, while the second type was responsible for the celestial interactions that caused planets to move along perfect, circular trajectories.
Newton was able to mathematically connect gravity with the ratios of planetary motion discovered by Kepler, thereby dispelling the false separation between the physical laws governing the Earth and the rest of the universe.
Summary of the Law of Universal Gravitation
Isaac Newton formulated the law of universal gravitation based on his observations of the Moon’s orbit around the Earth.
The gravitational pull exerted by the Earth
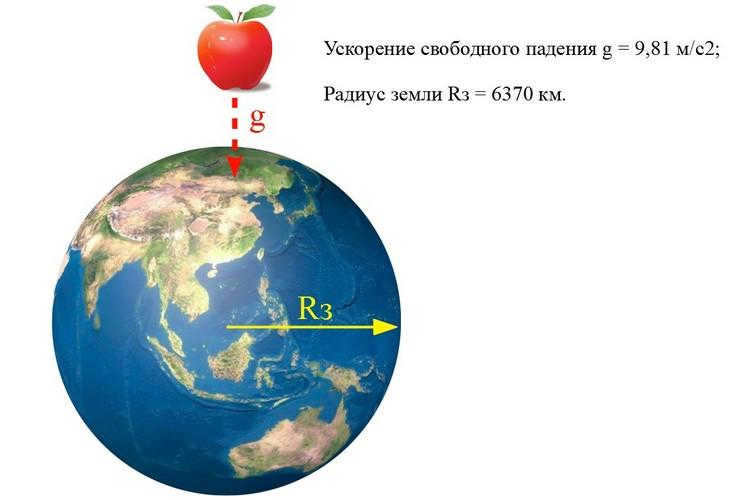
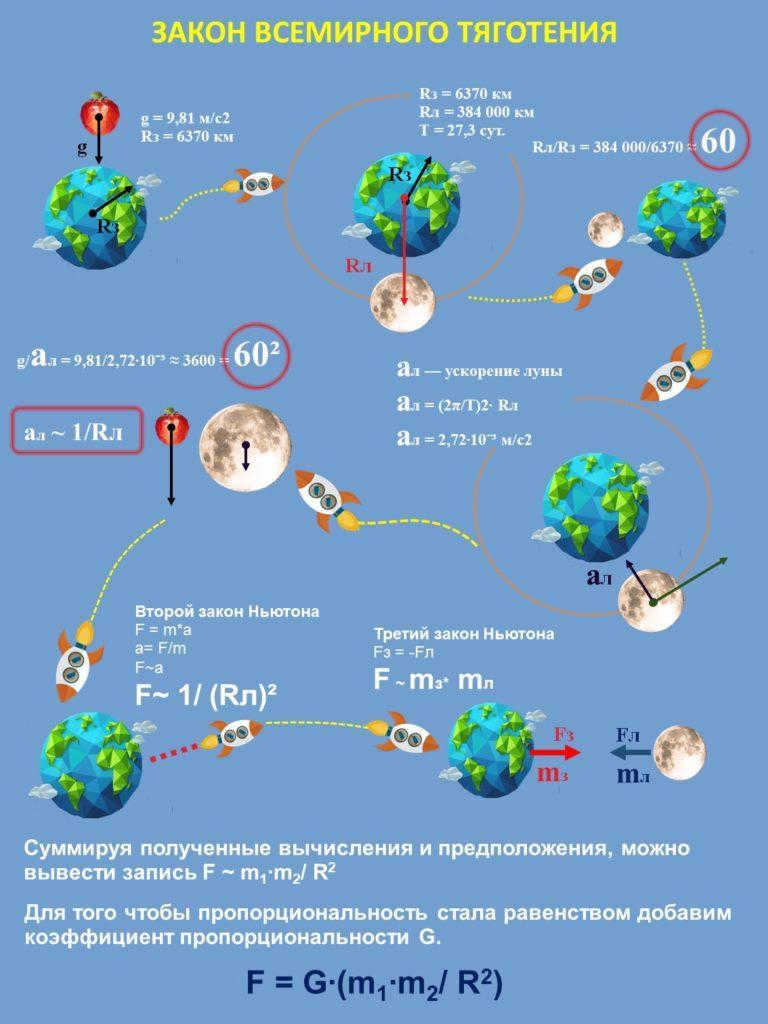
It is common knowledge that the Earth’s radius is RЗ = 6370 kilometers, and any object located on its surface experiences a gravitational acceleration of g = 9.81 m/s2.
Fascinating fact: scientists have discovered a correlation between g and latitude: at the equator, the value is slightly lower than the standard – 9.79 m/s2, while at the poles it reaches 9.83 m/s2.
Attraction of the Earth and the Moon
It is common knowledge that the Moon orbits the Earth, moving in a circular path with a radius of RM = 384000 kilometers and an orbital period of T = 27.3 days. To numerically estimate the magnitude of the Moon’s orbit in relation to the Earth’s radius, we can divide the given values by each other:
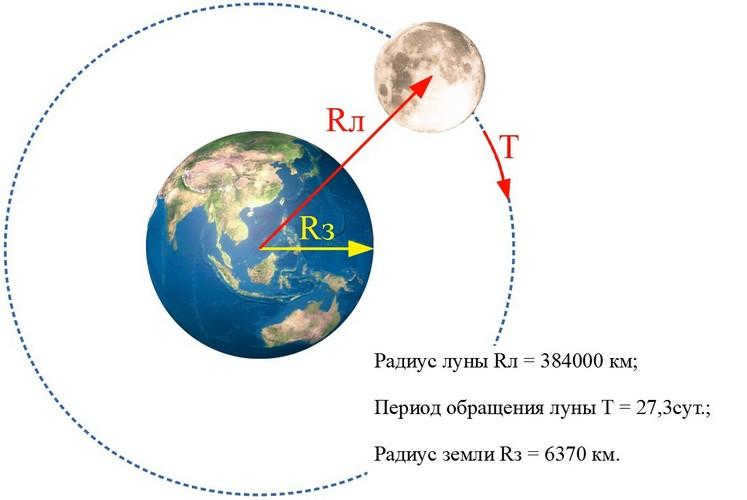
Based on the findings, it is clear that the distance from the celestial body to the satellite covers a span of 60 Earth radii.
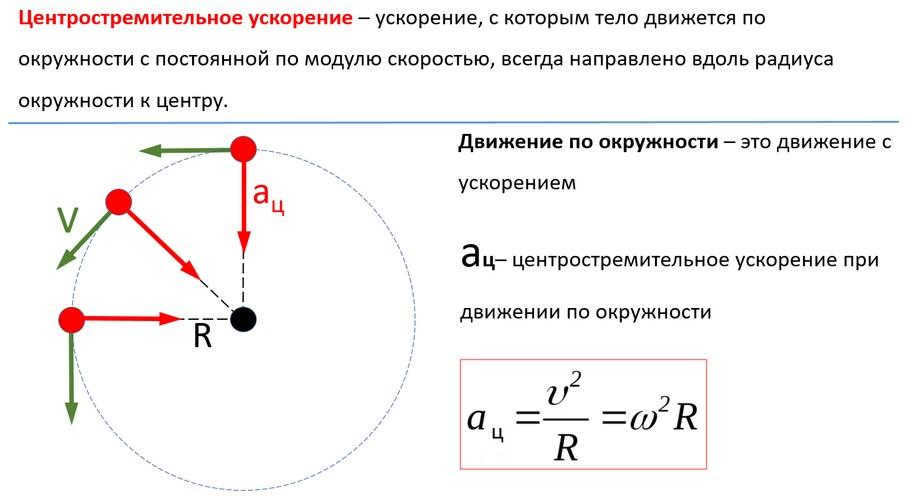
The Moon is pulled towards it by a force called centripetal force. It is understood that centripetal force can be calculated using the formula:
where ω represents the angular velocity of the motion;
R represents the radius of the circular path.
The angular velocity ω and the period of rotation T are related by the equation:
By substituting this equation into the acceleration formula and rearranging it by substituting variables for certain quantities, we can derive the following:
RL represents the orbit of the Moon or the distance from the Moon to the Earth.
Before obtaining the numerical value of the desired acceleration, it is necessary to convert the units of all components according to the International System of Units (SI):
- The period T = 27.3 days = 655.2 hours = 39,312 minutes = 2,358,720 seconds;
- The distance R = 384,000 kilometers = 384 ∙10^6 meters.
Therefore, the satellite is moving with an acceleration of:
aL = (2∙3.14 / 2,358,720)^2 ∙ 384 ∙10^6 = 2.72∙10^-3 m/s^2.
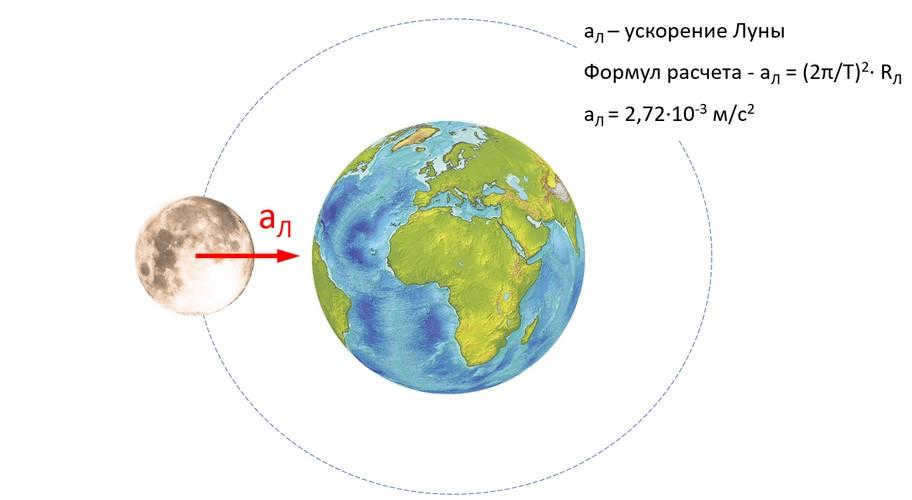
When comparing the obtained value with the value of g, we get:
g/aЛ = 9.81 / 2.72∙10 -3 ≈ 3600 = 60 2.
That means the acceleration experienced in the Moon’s orbit is 60 2 times less than the acceleration experienced on the Earth’s surface. Therefore, the satellite is 60 times farther away, supporting the assumption that the acceleration is inversely proportional to the distance squared:
Deriving the formula for gravitation using Newton’s second and third laws
In accordance with Newton’s second law, the acceleration experienced by a body, denoted as a, is directly proportional to the force applied to it, represented by F, and inversely proportional to its mass, denoted as m:
Based on this, it can be argued that the nature of the change in force is the same as the change in acceleration, as follows:
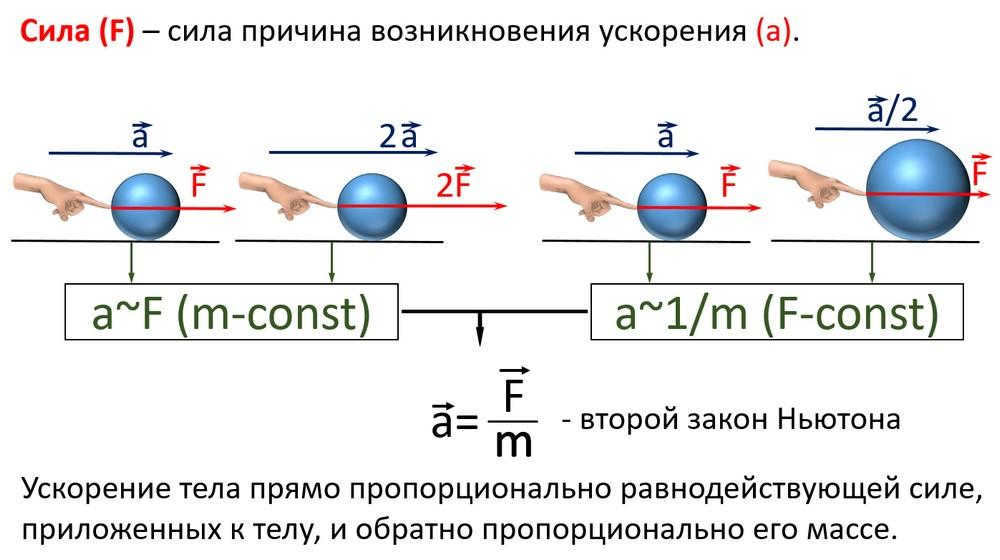
Given the assumption that acceleration is inversely proportional to the square of the distance, it follows that the force exerted on the body exhibits the same behavior:
Furthermore, Newton’s third law states that the interaction between bodies results in forces that are equal in magnitude but opposite in direction:
where F12 is the force exerted by the first body on the second;
F21 is the force exerted by the second body on the first.
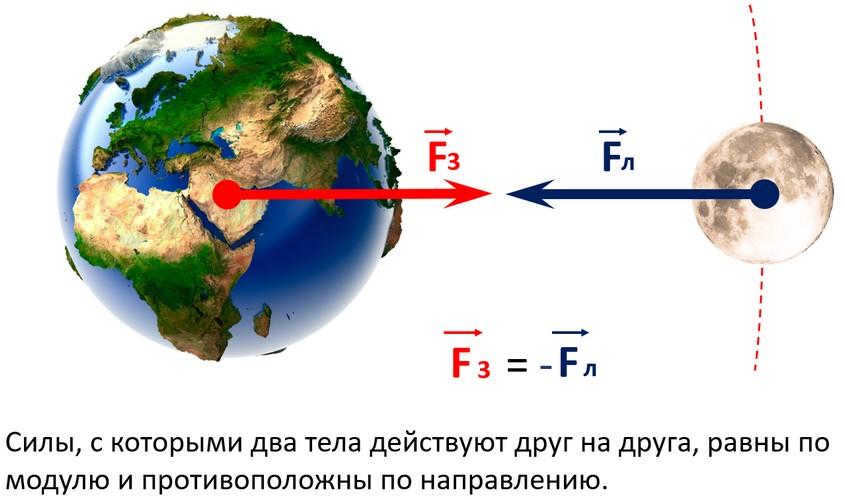

Thus, it can be said that not only does the Earth exert a force on its satellite, but the satellite also exerts a force on the Earth. According to Newton’s second law, the increase in force is directly proportional to the increase in acceleration and mass. Therefore, the attraction between the Moon and the Earth can be expressed as:
The multiplication symbol used here represents the conjunction of the mass of the Moon and the mass of the Earth, which both contribute to the attraction.
Universal gravitation formula
Summarizing the calculations and conjectures, we can derive the following notation:
However, since this relation applies not only to our planet and its satellite, but to all objects, the obtained form needs to be slightly transformed:
where F represents the gravitational force resulting from the interaction of two bodies;
m1,2 refers to the masses of the first and second body;
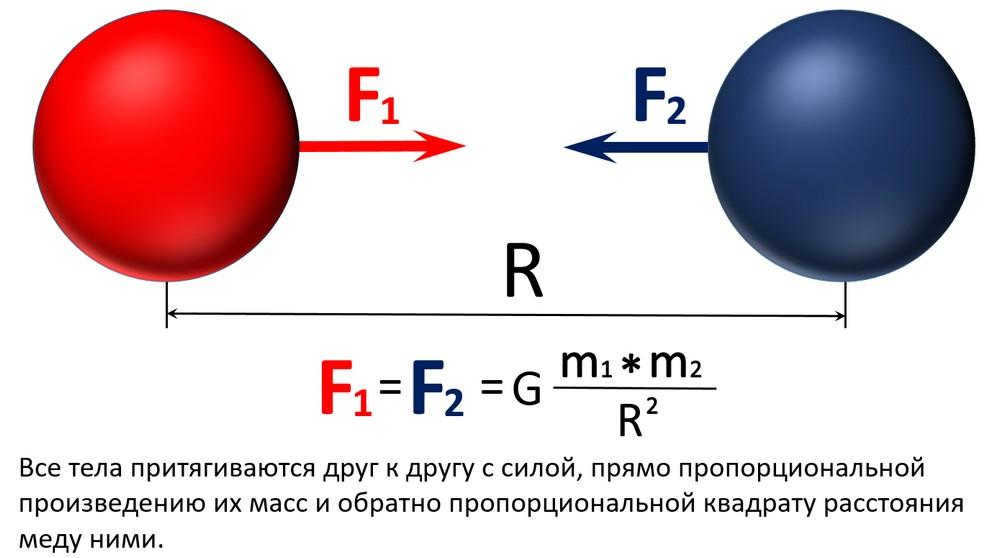
To achieve equality, a unique coefficient G, known as the gravitational constant, is necessary. Once incorporated, the resulting equation is referred to as the formula for the law of universal gravitation:
In the International System of Units (SI), the force of attraction is measured in newtons (N), which is the dimensionality of any force. Newtons are derived units that are formed by combining established basic units. Therefore, a newton can be defined as the ratio of a kilogram (kg) to the ratio of a meter (m) per second squared (s2), i.e. H = kg / (m/s2).
Prior to the adoption of the SI in 1960, the centimeter-gram-second (CGS) or absolute physical system of units was used, and force was measured in dynes. By definition, 1 dyne = 1 g / (cm/s2), which means that newtons and dynes differ by five orders of magnitude, i.e.: 1 N = 105 dynes.
Gravitational constant
The gravitational constant, denoted by G, is a fundamental physical constant that represents the force of attraction between two point masses each having a mass of one kilogram and separated by a distance of one meter. In the International System of Units (SI), G is defined as:
It is interesting to note that the value of this proportionality constant was not determined until 1798 by Henry Cavendish, a full 111 years after the publication of Isaac Newton’s groundbreaking work on gravity.
The Cavendish Experiment
In order to ascertain the value of the gravitational constant, a fascinating experiment was carried out, centering around the use of torsion scales. These remarkable devices consist of a sturdy steel wire, with a horizontal arm affixed to it. At the ends of this arm, two identical lead balls, each weighing 730 grams, are securely attached.
During the experiment, Cavendish conducted an investigation where he brought together small balls and large balls, with the larger ones weighing a total of 158 kilograms. These balls were suspended on a lever, and as the heavy balls were brought closer, a force of attraction between them arose. This force caused the lever to turn and the wire to twist, resulting in the generation of an elastic force that opposed the attraction of the balls. Eventually, the gravitational force and the elastic force of the twisted wire were balanced. Cavendish utilized optical devices to record the deflections of the balls and compared the forces acting on the system. Through this analysis, Cavendish was able to calculate the value of the coefficient.
The law of universal gravitation and the force of gravity
Newton’s mathematical model of gravity revealed that the force of gravity, a familiar and tangible phenomenon, is actually just a specific instance of the greater law of universal gravitation. According to this law, all celestial bodies, such as planets, stars, and asteroids, exert a gravitational force on each other.
To determine the magnitude of this force exerted by the Earth, we can utilize a formula that expresses a direct proportionality between the force and the mass of the object:

At the surface level, the acceleration of free fall is commonly accepted to be 9.81 m/s 2 . If an object is removed from the Earth’s surface, the value of g can be determined using the following formula:
where h represents the distance from the object to the ground.
Consequently, the influence of gravity on an object diminishes as its height increases.
Fascinating fact: if we consider the force of gravity acting on Earth as a unit, we can examine the gravitational pull on the surface of other celestial bodies. As a result, the greatest gravitational impact would be experienced on Jupiter’s surface (2.442), while the smallest would occur on the Moon (0.165).
When does the law of universal gravitation apply?
The law of universal gravitation, as formulated by Newton, has certain limitations in its application. It is only valid under the following conditions:
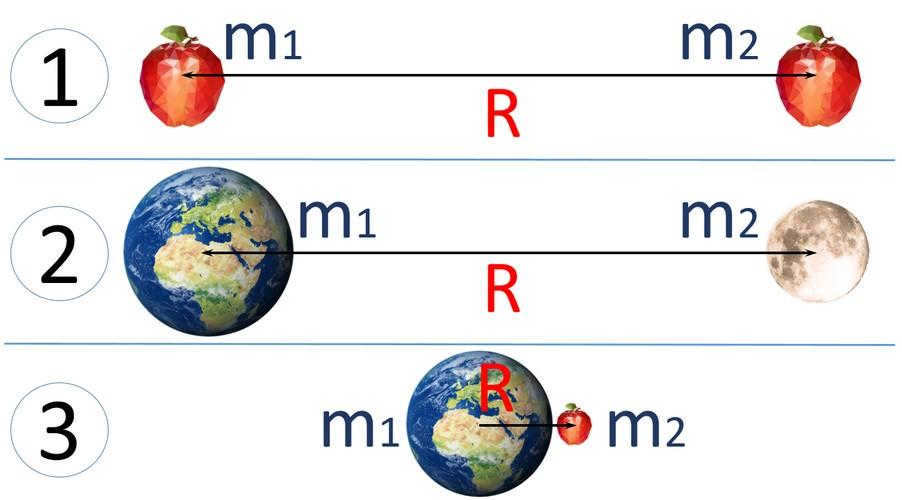
- The bodies involved can be treated as point masses, meaning their dimensions are so insignificant compared to the distance between them that they can be disregarded.
- The bodies have a spherical shape, indicating a uniform distribution of mass within them.
- One of the bodies is a large-sized sphere, while the other has significantly smaller dimensions.
If we want to describe the interaction between a ball and an infinitely long rod, the law of universal gravity cannot be applied. In this situation, the force of attraction will not be proportional to the square of the distance, but to its modulus. Similarly, when determining the gravitational force between an infinite plane and a body, the distance between them will not have any effect.
The principle of universal gravitation is a crucial concept in physics that has provided explanations and predictions for a wide range of natural phenomena. Some of these phenomena include:
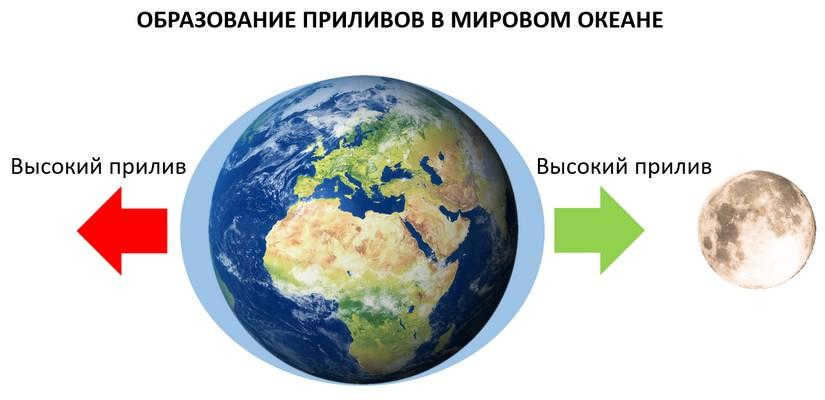
- The occurrence of tides;
- The ability to determine the precise timing and location of lunar and solar eclipses;
- The determination of the masses of celestial bodies such as the Sun and other astronomical objects;
- The understanding of the orbital paths followed by planets and their moons.
Exploration of Planets through the Universal Law of Gravitation
Following the identification of the gravitational phenomenon, astronomers and physicists have been able to utilize Newton’s law and Kepler’s principles to ascertain the paths of the observed planets within the solar system, providing their precise coordinates at any given moment. The accuracy of these calculations has been empirically confirmed through astronomical observations.

In the year 1781, an astronomer named William Herschel made a remarkable discovery. He found the seventh planet of our solar system, Uranus. Using a well-established method, Herschel calculated the path and orbit of this new planet. However, in the early 19th century, scientists noticed a discrepancy between the predicted coordinates and the actual position of Uranus. This led to the hypothesis that there might be another planet exerting gravitational influence on Uranus.
Then, in 1846, a young employee of the British Observatory named Johannes Galle made a groundbreaking discovery. Using theoretical calculations based on the observed deviations of Uranus, Galle predicted the existence of a new planet. This planet was later named Neptune.

An interesting fact is that the calculations that led to the discovery of Neptune were made independently by two scientists, John Adams and Urbain Leverrier.
Almost 100 years later, on February 18, 1930, a similar method was used to discover the ninth planet, Pluto, which is considered a dwarf planet due to its relatively small size and mass.
Every object in the universe experiences attraction. This law manifests itself in everyday life through various phenomena, such as leaves falling from trees, stones dropping, raindrops descending, and even mountain slumps and landslides.
Besides, the theory of gravity is evident through the existence of mass in each object – the energy that an object exerts on a surface to prevent it from descending further towards the Earth’s core.
Boundaries of applicability
Despite the fact that Newton’s law of universal gravitation provides an explanation for many phenomena, in the late 19th century, a discrepancy between the observed and calculated displacement of Mercury’s perihelion was discovered. This particular aspect of the planet’s motion could not be accounted for by the existing law, leading to the need for a new understanding of gravity.
Furthermore, at the turn of the century, the applicability of classical mechanics, which is based on Newton’s laws, was found to have limitations. It can only provide accurate results in situations where:
- the velocity of objects is significantly lower than the speed of sound;
- the size of objects is significantly larger than the size of atoms and molecules;
- the speed of gravity is assumed to be infinite.
Ever since the theory of gravity was first formulated, numerous scientists who disagreed with Newton’s scientific beliefs have endeavored to enhance his law. In the 19th century, various challenges arose that called into question the foundations of Newtonian physics, necessitating the introduction of modifications that could account for the discrepancies between observed and calculated results. In 1915, Albert Einstein formulated the General Theory of Relativity (GTR), which successfully accounted for the perihelion shift of Mercury and is now widely regarded as the most promising theory of gravity, supported by numerous experimental findings.
GTR has defined limitations in its applicability, such as its inability to account for quantum effects. As a result, a new theory was necessary to bridge the gap between Einstein’s theory of relativity and quantum mechanics. Despite their differing postulates, these two theories, quantum gravity, in particular, hold great promise in the realm of physical research.
Conclusions
Gravity is a phenomenon that causes all bodies in the universe to be mutually attracted. The force of attraction between two objects is directly proportional to their masses and inversely proportional to the distance between them.
After reading this article, one can quickly and accurately understand how the law of universal gravitation is formulated. However, it is important to remember that Newton’s formula is only valid for specific cases.
Furthermore, despite the existence of new hypotheses and confirmations, Newtonian mechanics, including the law of universal gravitation, remains the simplest and most accurate theory for describing natural phenomena within its limitations.
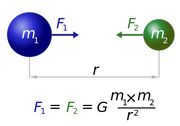
Newton’s Law of Universal Gravitation is a fundamental principle in classical mechanics that explains the gravitational interaction between two objects. This law, which was first discovered by Sir Isaac Newton in 1666, states that the gravitational force (F) between two material points with masses (m1 and m2) is directly proportional to the product of their masses and inversely proportional to the square of the distance (R) between them. In mathematical terms, it can be expressed as follows:
Characteristics of Newtonian gravity [ ]
When matter density ρ is distributed arbitrarily, the Poisson equation is satisfied by φ:
The solution to this equation can be expressed as:
where r represents the distance between the volume element dV and the point where the potential φ is defined, and C is an arbitrary constant.
The gravitational force acting on a material point with mass m in a gravitational field is determined by the potential using the equation:
A spherically symmetric object generates the same field outside its boundaries as a material point with the same mass positioned at the center of the object.
Accuracy of Newton’s law of universal gravitation [ ]
The precision of Newton’s law of universal gravitation has been experimentally evaluated to confirm the validity of the general theory of relativity. [1] Experiments that measured the quadrupole interaction between a rotating object and a stationary antenna demonstrated [2] that the deviation δ in the formula for the Newtonian potential, r – ( 1 + δ ), is less than ( 2 , 1 ± 6 , 2 ) ∗ 10 – 3 > at distances of a few meters. Other experiments have also confirmed that there are no modifications to the law of universal gravitation [3] .
In 2007, Newton’s law of universal gravitation was tested at distances smaller than one centimeter (ranging from 55 μm to 9.53 mm). Considering the experimental uncertainties, no deviations from Newton’s law were observed within the investigated distance range [4] .
Accurate laser measurements of the Moon’s orbit [5] have provided further evidence supporting the law of universal gravitation at the Earth-Moon distance, with a remarkable precision of 3 ⋅ 10 – 11 > .
A Brief History [ ]
In his groundbreaking work “1687) Isaac Newton derived the law of gravitation based on Kepler’s empirical laws known at that time. He demonstrated that:
- The observed movements of the celestial bodies indicate the existence of a central force;
- Conversely, a central force of gravity leads to elliptical (or hyperbolic) orbits.
Newton’s theory, in contrast to the hypotheses of his predecessors, possessed several significant distinctions. Newton not only published an assumed formula for the law of universal gravitation, but actually proposed a comprehensive mathematical model:
- The law of gravitation;
- The law of motion (Newton’s second law);
- A system of techniques for mathematical investigation (mathematical analysis).
When combined, this trio of concepts provides a comprehensive framework for studying the intricate movements of celestial bodies, thereby establishing the groundwork for celestial mechanics. Prior to Einstein, no major revisions were required for this model, although further development of the mathematical tools was necessary.
It should be noted that Newton’s theory of gravitation no longer strictly qualifies as a two-body problem. The planet does not simply orbit around the Sun; rather, both the Sun and the planet revolve around a shared center of gravity. This is because the planet not only experiences attraction from the Sun, but also exerts its own gravitational pull on the Sun. Thus, it became imperative to consider the mutual influence of the planets on one another.
During the 18th century, there was active debate and scrutiny surrounding the law of universal gravitation, as it faced opposition from supporters of the Descartes school. However, by the end of the century, it became widely acknowledged that the law of universal gravitation had the ability to accurately explain and predict the movements of celestial bodies. In 1798, Henry Cavendish conducted a direct experiment to test the validity of the law of gravitation in terrestrial conditions using highly sensitive equipment [9]. Furthermore, an important development occurred in 1813 when Poisson introduced the concept of gravitational potential and the Poisson equation, which allowed for the study of gravitational fields with arbitrary distributions of matter [10]. As a result, Newton’s law of gravitation became established as a fundamental law of nature.
Further development [ ]
General theory of relativity [ ]
After Isaac Newton’s theory of gravitation, physicists spent more than two centuries proposing various ideas to improve upon it. Finally, in 1915, Albert Einstein created the general theory of relativity, which successfully addressed all the challenges faced by Newton’s theory. It was discovered that Newton’s theory was actually an approximation of a more comprehensive theory, which applied under two specific conditions:
- The gravitational potential in the system being studied is not too large: φ c^2 ≪ 1 >>\ll 1>. In the solar system, this condition can be considered fulfilled for most motions of celestial bodies – even on the surface of the Sun, the ratio φ / c^2 > is only 2, 12 ⋅ 10^-6 12\cdot 10^>. The only noticeable relativistic effect is the mentioned perihelion shift [12].
- The velocities of motion in this system are negligible compared to the speed of light: v c ≪ 1 >\ll 1>.
In weak stationary gravitational fields, the equations of motion approach the Newtonian (gravitational potential). To prove this, we will demonstrate that the scalar gravitational potential in weak stationary gravitational fields satisfies the Poisson equation.
It is well-known (Gravitational potential) that in this case, the gravitational potential takes the following form:
Let’s determine the value of the energy-momentum tensor component T 44 > from the equations R i k = – ϰ ( T i k – 1 2 g i k T ) =-\varkappa (T_->g_T)> ,
where R i k > – T i k > , we can introduce the tensor for kinetic energy-momentum ρ u i u k u_> . By neglecting terms of the order u / c , we can set all components of T i k > , except T 44 > , to zero. The value of T 44 > is equal to T 44 = ρ c 2 =
ho c^> and therefore T = g i k T i k = g 44 T 44 = – ρ c 2 T_=g^T_=-
ho c^> . Consequently, the equations for the gravitational field can be expressed as R 44 = – 1 2 ϰ ρ c 2 <\displaystyle R_=->\varkappa
ho c^> . This is due to the formula

Let’s be honest, many of us didn’t fully comprehend the concept behind Newton’s law of universal gravitation during our school days. This is not surprising: the majority of mankind, save for a select few astronomers and physicists, were completely unaware of it until 1687. Even after its discovery, scientists spent the next 200 years diligently working to rigorously validate Newton’s brilliant theory. So, there’s absolutely no shame, even for an adult, in refreshing your understanding of this enigmatic force that draws all bodies in the Universe together, shapes the orbits of the planets in our solar system, influences the tides, propels the flow of rivers on Earth, and even led scientists to the discovery of the planet Neptune.
What is the history behind the discovery of the law of universal gravitation?
No more gravity?
If all objects in the Universe are subject to gravitational attraction, why do we only experience attraction to the Earth and not to other objects like refrigerators or each other? The key factors are mass and distance: when the mass of an object is small and the distance is large, we do not perceive any gravitational attraction. It is only when dealing with a massive object like the Earth that we truly feel the force of gravity, which is one of the most noticeable manifestations of universal gravitation.
The law of universal gravitation asserts that any two objects are drawn towards each other with a force that is directly proportional to the mass of each object and inversely proportional to the square of the distance between them.
The equation employed for this calculation is: F = G ∙ (m1 ∙ m2) / R², with m representing the mass, R representing the distance between the entities, and G representing the gravitational constant, whose value has been determined through experimental means. This constant G is exceedingly minuscule (6.67 ∙ 10 -11 m³ / (kg ∙ s²)) – thus explaining why the force exerted on bodies with negligible mass goes unnoticed by us.
Did Newton make any discoveries?
Neptune was discovered with the help of Newton
Physicists did not fully accept Newtonian theory as the basis of celestial mechanics until the 18th century. Newton’s law of universal gravitation was a significant breakthrough for astronomers because it provided a mathematical explanation for almost everything that occurs in the universe. However, Newton’s most significant contribution to astronomy was the discovery of Neptune in 1846, the farthest planet from Earth and the first to be found through mathematical calculations. This monumental discovery followed the observation of Uranus in 1781 by English astronomer William Herschel. Astronomers studying Uranus for many years were puzzled by the fact that its actual orbit did not match the calculated one. This discrepancy led them to believe that there must be another planet exerting its gravitational influence on Uranus. French mathematician Urbain Leverrier used Newtonian mechanics to calculate the location of the eighth planet and pointed astronomers in the right direction. However, even in the early 20th century, there were still unanswered questions that Newton’s law of gravitation could not explain. How does gravity extend through the vast expanse of the universe? Where does it originate from? How does it act instantaneously and at any distance? Can the gravitational paradox be resolved? Why is there a discrepancy between the observed and theoretical motion of Mercury’s perihelion? These cosmological mysteries were ultimately addressed by Albert Einstein’s general theory of relativity, which he proposed in 1915. But that, as they say, is another story.





