Every day, as it emerges from the eastern horizon, the Sun traverses the sky and ultimately sets in the west.
In the Northern Hemisphere, this movement is from left to right, while in the Southern Hemisphere it goes from right to left. At noon, the Sun reaches its peak altitude, or as astronomers put it, culminates. The upper culmination occurs at noon, while there is also a lower culmination at midnight. In our moderate latitudes, the lower culmination of the Sun is not observable, as it takes place below the horizon. However, beyond the Arctic Circle, where the Sun may not set in the summer, both the upper and lower culmination can be witnessed.

When the Sun reaches the geographic pole, it follows a path that is nearly parallel to the horizon. During the vernal equinox, the Sun gradually rises higher and higher in the sky, tracing circles above the horizon. On the day of the summer solstice, it reaches its highest point, with an elevation of 23.5 degrees. For the next quarter of the year, leading up to the autumn equinox, the Sun begins to descend. This period is known as polar day. Following polar day, there is a six-month period known as polar night.
During the equinoxes, the Sun is positioned exactly on the celestial equator. On these specific days, it rises from an eastern point and sets at a western point. It is important to note that the apparent height of the Sun is always greater than its true height due to refraction caused by the Earth’s atmosphere. As a result, the Sun appears to rise earlier and set later than it actually would without the presence of the atmosphere.
Throughout the year, the Sun follows a small circular path on the celestial sphere that is parallel to the celestial equator. However, its position relative to the celestial equator changes over time, moving both northward and southward. The length of the day and night portions of its path are not equal, except during the equinoxes when the Sun is precisely on the celestial equator.
The Sun’s movement is gradual, at a rate of approximately 1° per day, as it traverses the stars to the left. This gradual shift allows us to observe how the view of the celestial sky changes throughout the year. These changes are a direct result of the Earth’s orbit around the Sun. The Sun’s visible path during its annual journey against the backdrop of stars is known as the ecliptic, and the time it takes to complete this rotation along the ecliptic is called the sidereal year. The duration of a sidereal year is approximately 365 days, 6 hours, 9 minutes, and 10 seconds, or 365.2564 average solar days.
The primary point among the four points of the ecliptic is known as the vernal equinox point. It serves as the starting point for measuring one of the celestial coordinates, known as the direct ascent. Additionally, it is used to calculate the sidereal time and the tropical year, which is the time it takes for the center of the Sun to pass through the vernal equinox point twice consecutively. The tropical year is responsible for determining the change of seasons on our planet. However, due to the precession of the Earth’s axis, the vernal equinox point moves slowly among the stars, causing the duration of the tropical year to be shorter than that of the sidereal year. Specifically, it is approximately 365.2422 average solar days.
The variation in the Sun’s path along the ecliptic, which occurs due to fluctuations in the velocity of the Earth’s elliptical orbit around the Sun, results in varying durations of the seasons. In the Northern Hemisphere, spring and summer are extended by six days compared to fall and winter. On July 2-4, the Earth is positioned 5 million kilometers further from the Sun than on January 2-3, causing it to orbit at a slower pace in accordance with Kepler’s second law. Even though the Northern Hemisphere receives less heat from the Sun during the summer, the summer season there is longer than winter. As a result, the Northern Hemisphere of the Earth experiences higher temperatures than the Southern Hemisphere.
The appearance of the moon is subject to change. It does not emit light on its own, therefore we can only observe the illuminated surface, known as the day side, in the sky. As the moon moves from west to east, it eventually catches up to and surpasses the Sun in a month’s time.
During this process, various lunar phases occur, including the new moon, first quarter, full moon, and last quarter.
During a new moon, the Moon is not visible even with the help of a telescope. It is positioned in the same direction as the Sun, either above or below it, and its unlit hemisphere is facing the Earth. After one or two days, when the Moon moves away from the Sun, a thin crescent shape can be seen for a few minutes before it sets in the western part of the sky, against the backdrop of the evening sky. The Greeks referred to the first appearance of this crescent shape after the new moon as neomenia, meaning “new Moon”. In ancient times, this moment was considered the start of a new lunar month.
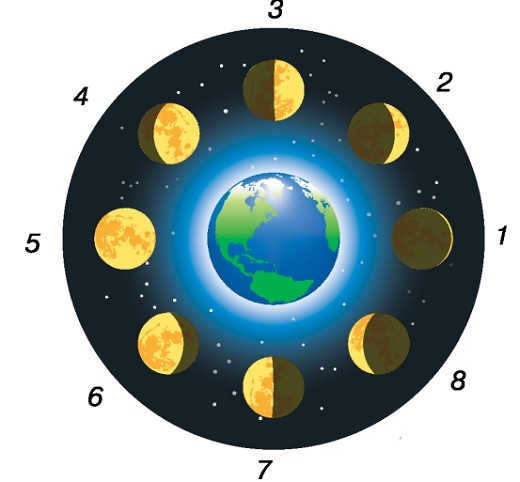
The Phases of the Moon.
1 – new moon: The Moon is not visible.
2 – young Moon: The Moon’s first appearance in the sky after the new moon, taking the shape of a narrow sickle.
3 – quarter: Half of the Moon is illuminated.
4 – waxing Moon.
5 – full moon: The entire Moon is illuminated.
6 – waning Moon.
7 – last quarter of the Moon: Half of the Moon is illuminated once again.
8 – Old Moon.
Following a period of 7 days and 10 hours following the occurrence of the new moon, a phase known as the first quarter ensues. At this point, the Moon has shifted its position from the Sun by 90°. Consequently, only the right half of the Moon’s disk becomes illuminated by the Sun’s rays. As the Sun descends below the horizon, the Moon can be observed in the southern region of the sky and ultimately sets around midnight. Continuing its eastward trajectory away from the Sun, the Moon becomes visible in the eastern part of the sky during the evening hours. It sets after midnight and with each passing 24-hour period, its setting time becomes progressively later.

Sometimes, during the time leading up to and following the occurrence of the new moon, it is possible to observe the faint, ashy glow of the moon. This dim illumination on the night portion of the lunar sphere is simply sunlight reflected by the Earth onto the Moon. As the crescent shape of the moon expands, the ashy glow gradually diminishes and eventually becomes undetectable.
As the crescent shape of the moon continues to shrink, the Moon itself gradually moves closer to the Sun from the right (western) side. The pale crescent becomes visible in the eastern sky during the morning hours, appearing later each day. The ashy glow of the moon at night becomes visible once again. The angular distance between the Moon and the Sun decreases from 90 degrees to 0 degrees. Eventually, the Moon catches up to the Sun and once again becomes invisible. The next occurrence of the new moon takes place, marking the end of the lunar month. The entire lunar cycle spans approximately 29 days, 12 hours, 44 minutes, and 2.8 seconds, or nearly 29.5 days.
The duration of time between successive phases of the Moon that share the same name is referred to as the synodic month. Hence, the synodic period is linked to the observable position of a celestial object (in this instance, the Moon) in relation to the Sun.

The Moon’s trajectory across the celestial sphere is relatively close to the ecliptic, causing the full Moon to ascend from below the horizon at sunset and roughly follow the same path it traversed six months earlier. During the summer season, the Sun ascends to great heights in the sky, while the full Moon remains relatively close to the horizon. Conversely, in winter, the Sun sinks low on the horizon, allowing the Moon to ascend to greater heights and cast a longer illumination on the winter landscapes, resulting in a blue tint to the snow.
The Moon completes its orbit around the Earth in approximately 27 days, 7 hours, 43 minutes, and 11.5 seconds, as it moves in relation to the stars. This specific time period is known as the sideric (derived from the Latin word “sideris,” meaning star) or sidereal month. It is worth noting that the sideric month is slightly shorter than the synodic month. To further understand this phenomenon, let’s examine the Moon’s motion from one new moon to the next. In a span of 27.3 days, the Moon completes a full revolution around the Earth, returning to its original position among the stars. However, during this time, the Sun has already progressed eastward along the ecliptic. Only when the Moon catches up with the Sun will the next new moon occur. This catch-up process typically takes an additional 2.2 days.
A lunar eclipse – is an astronomical event that amateur photographers can easily capture. When a lunar eclipse occurs, a round and red object, resembling a large colored glass disk, slowly moves across the edge of the full Moon over the span of an hour. Eventually, the entire Moon becomes covered in this red hue. The Moon stays in this state for a significant duration before the red circle starts to slide off its right side.

The Eastern sages discovered the reason for lunar eclipses many thousands of years ago, but this knowledge was kept as a secret by the priests. However, the Greek scientists, specifically Aristotle, were able to understand and reveal the wisdom of the Chaldeans.
Aristotle clearly articulated this truth and drew a crucial conclusion: the round cross-section of the shadow cone in an eclipse indicates that our Earth is round and can only be a sphere. This was the first, but not the sole, evidence supporting the Earth’s sphericity.
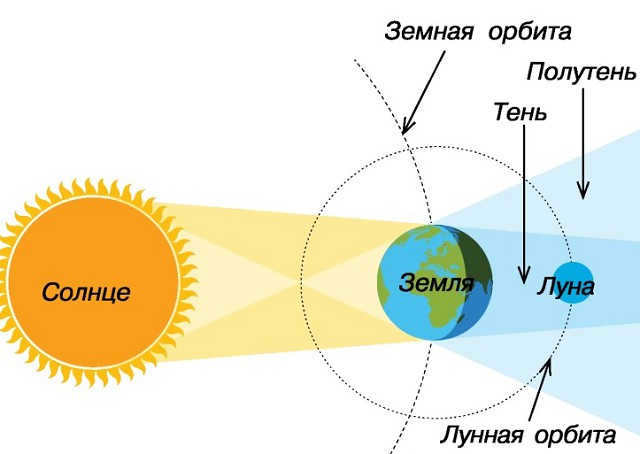
In the event that the Moon’s orbital plane were to align with the Earth’s orbital plane (known as the ecliptic plane), lunar eclipses would occur every full moon, approximately every 29.5 days. However, the Moon’s monthly path deviates from the ecliptic plane by 5°, causing it to only intersect the “circle of eclipses” at two specific points each month. These points, known as the nodes of the lunar orbit, present the only opportunities for a lunar eclipse to occur. Therefore, for a lunar eclipse to take place, two conditions must coincide: a full moon and the Moon’s proximity to one of its orbital nodes.
Depending on the proximity of the Moon to the orbital node during the eclipse, it can either traverse the center of the shadow cone, resulting in a maximized eclipse, or pass along the edge of the shadow, resulting in a partial lunar eclipse. The Earth’s shadow cone is encompassed by a penumbra, a region of space that only receives a portion of the sun’s rays that are not obstructed by the Earth. This is why penumbral eclipses occur. They are also documented in astronomical calendars, although these eclipses cannot be distinguished by the naked eye. Only a camera and photometer can detect the darkening of the Moon during the penumbral phase or penumbral eclipse. When a full moon occurs far from the nodes of the lunar orbit, the Moon traverses above or below the shadow, and no eclipse takes place.

Lunar eclipses occur during full moons, when the Moon is positioned directly behind the Earth, causing our planet’s immense shadow to cast upon it, obscuring the sunlight.
In ancient times, Eastern priests, while not fully comprehending the phenomenon, diligently recorded both total and partial lunar eclipses. On the surface, the eclipse schedule appears random, with some years having three lunar eclipses while others have none. Additionally, lunar eclipses can only be seen from the half of the world where the Moon is above the horizon during that time, meaning that from any given location on Earth, such as Egypt, only slightly more than half of all lunar eclipses can be observed.
However, for diligent observers, the sky eventually unveiled a fascinating secret: every 6585.3 days (known as a saros), an average of 28 lunar eclipses take place all over the Earth. Over the next 18 years, 11 days, and 8 hours (which is the exact number of days), all eclipses will recur according to the same pattern. The only thing left to do is to add 6585.3 days to the date of each eclipse. This is how ancient Babylonian astronomers mastered the art of predicting eclipses through “repetition.” In Greek, this system is known as “saros.” With saros, it becomes possible to calculate eclipses hundreds of years in advance.
As astronomers delved deeper into studying the Moon’s orbital motion, they not only became capable of determining the date of an eclipse using saros, but also the precise time at which it begins.
Solar eclipses
The Sun and Moon have a unique relationship in the sky during a solar eclipse. The Moon, being 400 times smaller than the Sun and positioned 400 times closer to it, creates the illusion that they are equal in size. As a result, during a total solar eclipse, the Moon effectively blocks out the bright surface of the Sun, allowing for the observation of the entire solar atmosphere.
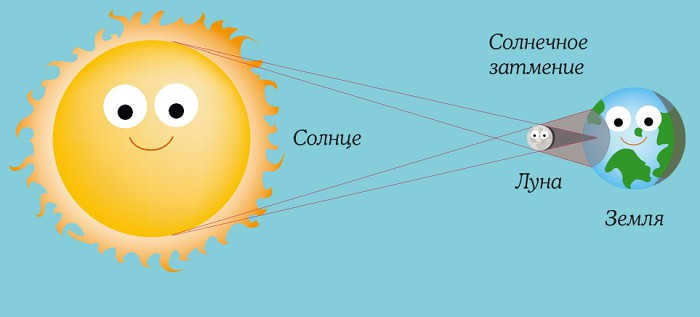
In order to comprehend when and how a solar eclipse takes place, it is necessary to examine the Earth and Moon from a different viewpoint. When the Moon passes between the Sun and the Earth, it is unable to completely block out the Sun’s light. Instead, the Moon’s short shadow creates a small dark spot on the Earth. This is the only location where a total solar eclipse can be witnessed at that particular moment. However, since the Moon is constantly moving in its orbit and the Earth is rotating, the shadow creates a narrow strip on the Earth, no wider than 270 kilometers, where a total eclipse can be seen. If the shadow’s path is more than 3-4 thousand kilometers away from us, we will not be able to observe the eclipse. Similarly, if we are situated near the edge of the total eclipse zone, in the penumbra region, only a portion of the Sun will be obscured by the Moon, resulting in a partial eclipse.

If the Moon is far away from the Earth on the day of the eclipse, its visible disk will be small and it won’t be able to fully cover the Sun. As a result, during the middle of the eclipse, the edges of the Sun will peek out from behind the Moon, making it difficult to see and capture the corona. This type of eclipse is called an annular eclipse.
In modern times, astronomers can accurately calculate eclipses for thousands of years in the past and hundreds of years in the future. Historical records of eclipses help historians accurately date events that took place on the same day and year as the eclipse.
Even though lunar eclipses are less frequent than solar eclipses on Earth, total solar eclipses are incredibly rare in a specific location, occurring on average once every 300 years. For instance, throughout the entire history of Moscow, it has experienced four total solar eclipses: in 1140, 1450, 1476, and 1887. The next total eclipse visible to Muscovites will occur on October 16, 2126. Astronomical calendars include maps of the total eclipse path and surrounding areas for interested experts and amateur astronomers to plan their expeditions ahead of time instead of relying solely on nature’s timing.
A solar eclipse is a remarkable event in which the Moon aligns between the Sun and the observer on Earth, resulting in the Moon’s shadow being cast on the Earth’s surface.

The occurrence of a total solar eclipse provides an ideal opportunity to observe the solar atmosphere, including the brilliant corona and the vibrant chromosphere, with its soaring prominences. However, astronomers are able to observe these phenomena even during a typical day by using a solar filter on their telescopes.
Even during a total solar eclipse, the Sun’s light is still able to illuminate the atmospheric layers near the horizon, creating a phenomenon similar to the dawn or sunset. This effect is known as the “dawn ring” and can be seen almost completely encircling the horizon.

Photographing solar eclipses can be challenging due to the significant difference in lighting between the partial and total phases, as well as the relatively short duration of the total phase, which typically lasts only a few minutes.
Observable movements of planets
The Moon is the first celestial body that humans noticed moving against the backdrop of the fixed constellation pattern. Its rapid movement allows us to see its motion within a single night.
Each hour, the Moon shifts its position in relation to the stars by the width of its apparent diameter, as it participates in the Earth’s daily rotation around its axis. The Moon’s movement among the stars is in the opposite direction of its daily rotation.
It is more challenging to detect the Sun’s movement due to its daytime brightness, which makes it difficult to see the faint stars in the background. However, by observing seasonal changes in the night sky, people have come to realize that the Sun also moves in relation to the stars, albeit at a much slower pace than the Moon.
Even before this realization, astronomers had discovered prominent celestial bodies, known as planets, whose movement among the stars was undeniable. These planets were named after gods and goddesses of the Roman pantheon during the Roman era, aligning with their distinct appearances and motions.

The motion of the planets in relation to the stars appears to be more intricate compared to the motion of the Sun and Moon. While initially following the same path as our primary celestial bodies, the planets eventually decelerate, come to a halt, reverse their direction, and then, after another pause, revert back to their original trajectory. This west-to-east movement is referred to as a direct path, while an east-to-west motion is known as a retrograde path. The instances of directional changes are termed as standstills. If one were to map out this course, it would form a loop.
Once upon a time, highly intricate mechanical systems were created in order to account for these peculiar movements. Religious and philosophical concepts regarding the organization and harmony of the world have long held sway over the human mind. Specifically, the only motion deemed worthy of celestial objects was deemed to be uniform circular motion. As a result, the scientific community for many centuries adhered to the geocentric system devised by Alexandrian Claudius Ptolemy, which sought to explain the apparent movements of the planets as a combination of such uniform circular motions. In this system, the fixed Earth was positioned at the center of the universe, with the centers of the circles on which the planets moved uniformly rotating around it. However, this model failed to accurately account for the observed planetary motions and had to be complicated by the addition of new circles. It took the brilliance of Copernicus and Kepler to accurately describe the actual movements of the planets around the Sun.
Therefore, when Venus and Earth align with the Sun and are on the same side, Venus surpasses Earth in its orbital movement and appears to move backwards among the stars in the Earth’s sky. Similarly, when Earth and Mars are in this position, Earth overtakes its outer neighbor and causes it to appear to move backwards in the sky.

The size of the loop varies based on the planet’s distance from Earth: the larger the distance, the smaller the loop. It’s important to note that the planets move in loops instead of linear paths because their orbits are not aligned with the ecliptic plane, which is the plane of Earth’s orbit.
If the Earth’s pole “moves” among constellations, it implies that the positions of these constellations relative to the stars and the celestial equator, as well as the point of the vernal equinox, from which astronomers calculate celestial coordinates, change accordingly. During the 2nd century BC, Hipparchus meticulously measured the coordinates of approximately 900 stars, creating a comprehensive star catalog. He then compared his observations with a catalog compiled a century earlier and noticed that the coordinates of the stars had shifted slightly, giving the impression that the entire celestial sphere had shifted sideways. This discovery led to the understanding of precession.

At the moment, there are additional cumulative discounts (ranging from 2% to 25%) that can be availed by 58,741 educational institutions. To determine the specific discount applicable to all staff members of your educational institution, please log in to your personal Infoworks account.


Enrich your knowledge with our professional development course
Master the essentials of crisis psychology
We are pleased to offer an additional discount for your educational institution (the amount of discount depends on the number of your colleagues who have completed Infowork courses).
At present, there are 58,741 educational institutions that qualify for cumulative discounts ranging from 2% to 25%. To discover the applicable discount for all staff members of your educational institution, simply log into your personal Infoworks account.


Advanced Training Program
Utilizing Interactive Educational Platforms with a Focus on the Moodle Platform
We have the ability to include your institution’s discount in addition to our current discount offer (percentage depends on the number of colleagues from your institution who have completed Infoworks courses).
Currently, 58,741 educational institutions are benefiting from additional discounts ranging from 2% to 25%. To determine the discount available for all employees at your institution, please log in to your personal Infoworks account.


Getting Ready for the Literature USE. Exploring the Creative Legacy of I. S. Turgenev
An Overview of the Presentation by Individual Slides:


Slide 1: The Sun’s yearly trajectory across the celestial sphere. Miass, Chelyabinsk Oblast. MCOE “SCHOOL № 9” physics and astronomy teacher, Ms. Deryabina.

Slide 3 features the renowned Polish astronomer, Nicolaus Copernicus (1473-1543).
He provided an explanation for the observable motions of the celestial bodies through the Earth’s rotation on its axis and the planets’ orbits around the Sun.
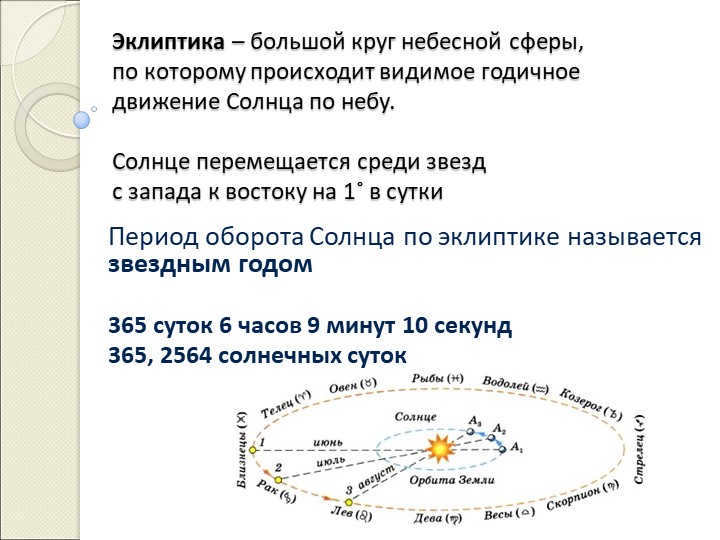

On slide 4, the ecliptic is described as the great circle of the celestial sphere that the Sun follows as it moves across the sky throughout the year.
The Sun’s motion among the stars occurs from west to east at a rate of 1˚ per day. This complete revolution along the ecliptic is known as a sidereal year.
It takes 365 days, 6 hours, 9 minutes, and 10 seconds, or 365.2564 solar days, for the Sun to complete one revolution along the ecliptic.
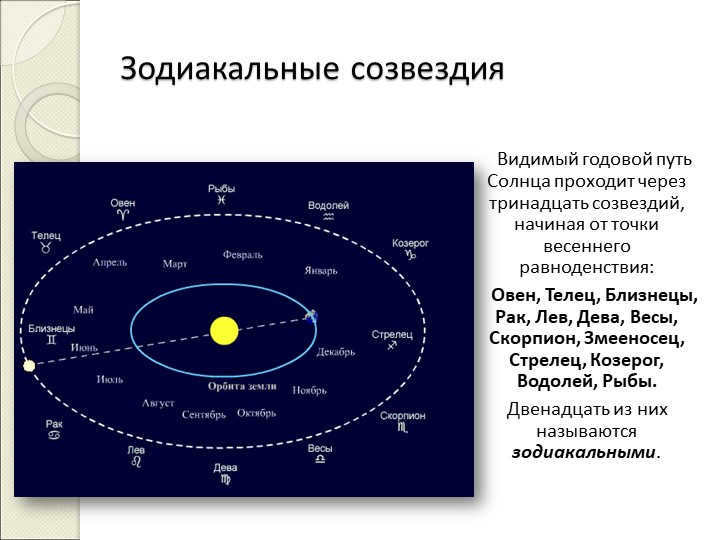
Slide 5: The constellations of the zodiac
The annual path of the Sun is visible as it passes through thirteen constellations. This journey begins at the vernal equinox and includes Aries, Taurus, Gemini, Cancer, Leo, Virgo, Libra, Scorpio, Serpentor, Sagittarius, Capricorn, Aquarius, and Pisces.
Out of these thirteen constellations, twelve are known as the zodiacal constellations.
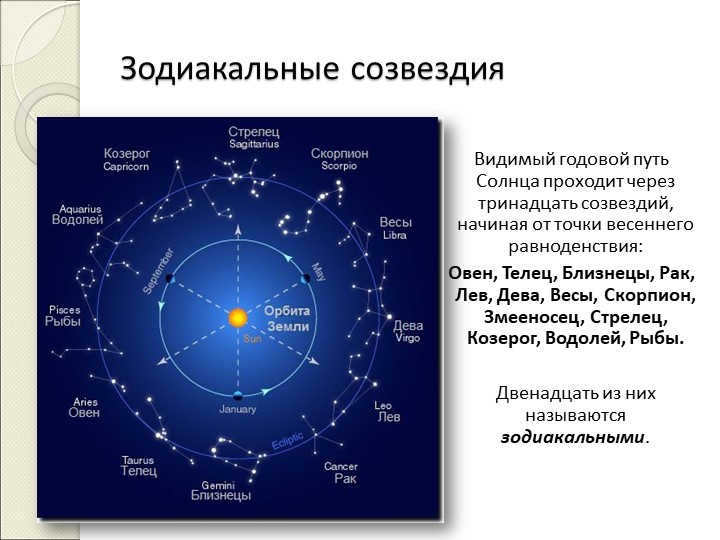
On slide 6, we can observe the zodiacal constellations. These constellations are the thirteen that the visible annual path of the Sun passes through, beginning at the vernal equinox. The zodiacal constellations include Aries, Taurus, Gemini, Cancer, Leo, Virgo, Libra, Scorpio, Serpentor, Sagittarius, Capricorn, Aquarius, and Pisces.
Out of these thirteen, twelve are referred to as zodiacal constellations.


7 slide The celestial equator and the ecliptic are inclined at an angle of 23˚27̕.
Where do the ecliptic and the celestial equator intersect?
The time interval between two consecutive passages of the Sun through the point of the vernal equinox is known as the tropical year.
The tropical year is shorter than the sidereal year and has a duration of 365.2422 solar days.
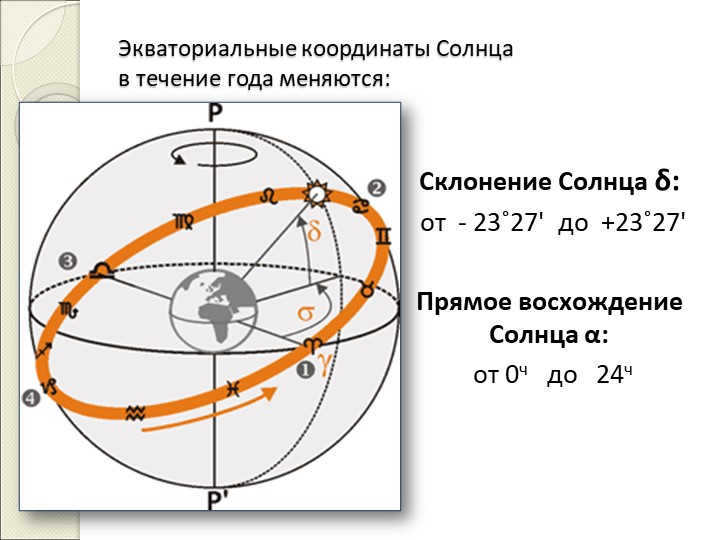
Throughout the year, the Sun’s equatorial coordinates undergo changes:
The Sun’s declination δ ranges from -23˚27′ to +23˚27′.
The Sun’s right ascension α ranges from 0h to 24h.
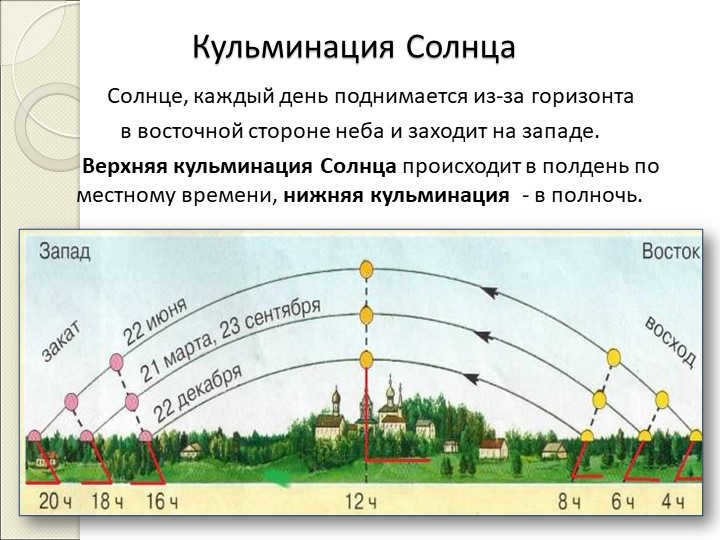
Slide 11: The Sun’s Pinnacle
Every day, the Sun emerges from the horizon
on the eastern side of the sky and descends in the west.
The Sun reaches its highest point in the sky at noon local time and its lowest point at midnight.
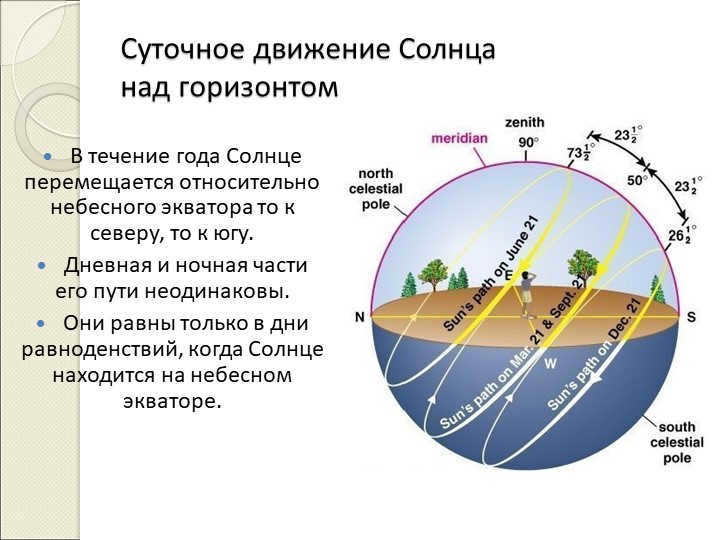
During the course of a year, the Sun undergoes a daily motion above the horizon. This motion is not uniform, as the Sun moves relative to the celestial equator, first to the north and then to the south. The path of the Sun during the day and night is not symmetrical, with the only exception being the days of equinoxes when the Sun is positioned directly on the celestial equator.
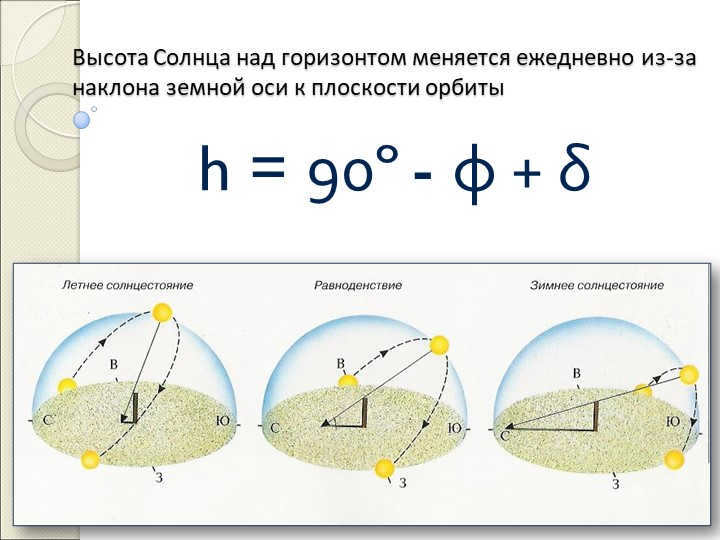

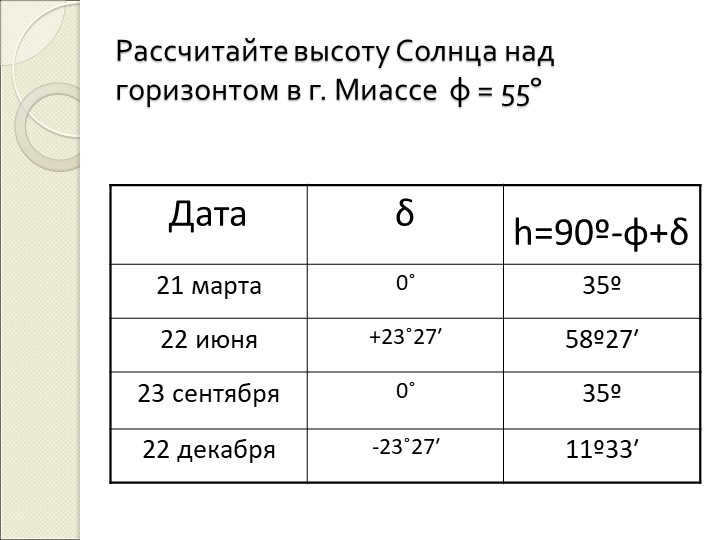
Slide 13: The Sun’s altitude above the horizon varies on a daily basis as a result of the Earth’s axis being tilted relative to the plane of its orbit. The formula for calculating the Sun’s height above the horizon is h = 90° – φ + δ.
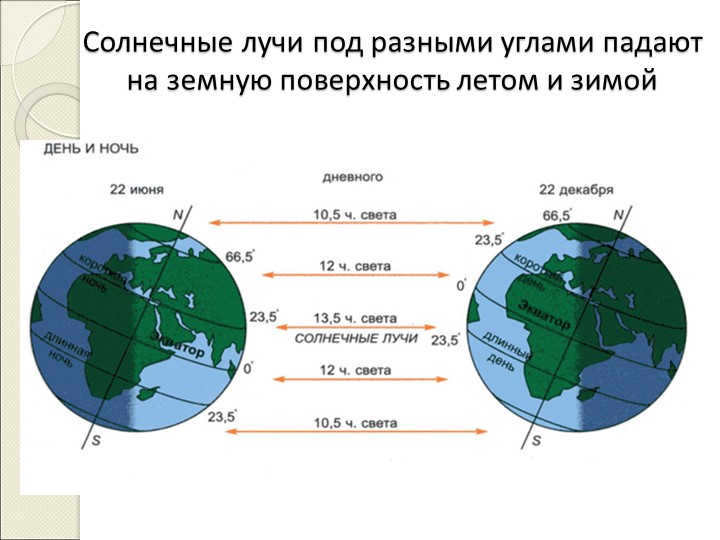

Slide 16: North Pole of the Earth
φ = 90º
On March 21st, the sunrise occurs at this location.
The Sun follows a spiral path that is nearly parallel to the horizon line, gradually ascending higher and higher.
On June 22nd, the Sun reaches its maximum height above the horizon at 23º 27'.
Afterwards, the Sun descends along a spiral path that is almost parallel to the horizon line.
On September 23rd, the sunset takes place.
From March 21st to September 23rd, it is the polar day in this region.
From September 23rd to March 21st, it is the polar night in this region.

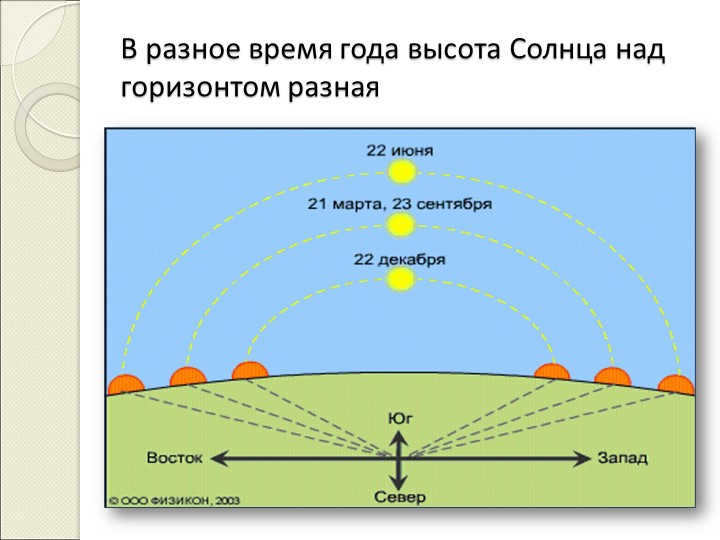
In the Arctic Circle, which is located at a latitude of 66º33', there is a phenomenon that occurs once a year for exactly 24 hours. This phenomenon is known as the polar day and it happens on June 22. During this day, the sun remains above the horizon for the entire 24-hour period, resulting in continuous daylight. On the other hand, on December 22, the Arctic Circle experiences polar night, where the sun remains below the horizon for the entire 24 hours, resulting in continuous darkness.
Additionally, on March 21 and September 23, the day and night are equal in duration, lasting 12 hours each. These are known as the equinoxes. However, on all other days of the year, the duration of the day and night in the Arctic Circle is not equal.

Slide number 18 at Middle latitudes
with latitude φ ranging from 66º33' to 23º27'
There are only two occasions throughout the year when the duration of the day is equal to that of night, lasting for 12 hours each:
March 21 – the date of the vernal equinox
September 23 – the date of the autumnal equinox.
On these specific days, the Sun rises in the east and sets in the west.
June 22 – the day with the longest duration of daylight and the maximum altitude of the Sun above the horizon
December 22 – the day with the shortest duration of daylight and the minimum altitude of the Sun above the horizon

On June 22nd, the Sun reaches its highest point at the northern tropic with a φ angle of 23°27′. This event, known as the summer solstice, occurs once a year. For the rest of the year, the Sun culminates to the south. During the summer solstice, the day and night are equal, with 12 hours of daylight.


Slide 23: Earth’s Equator
φ = 0°
Every day is equal to 12 hours of night.
The Sun reaches its highest point twice a year:
March 21 and September 23, during the vernal and fall equinoxes.

24 Slide Learn about the occurrence of the Sun’s daily motion at different points on Earth:
At the south pole of Earth
At the circle of latitude known as the southern polar circle
At the line of latitude known as the southern tropic

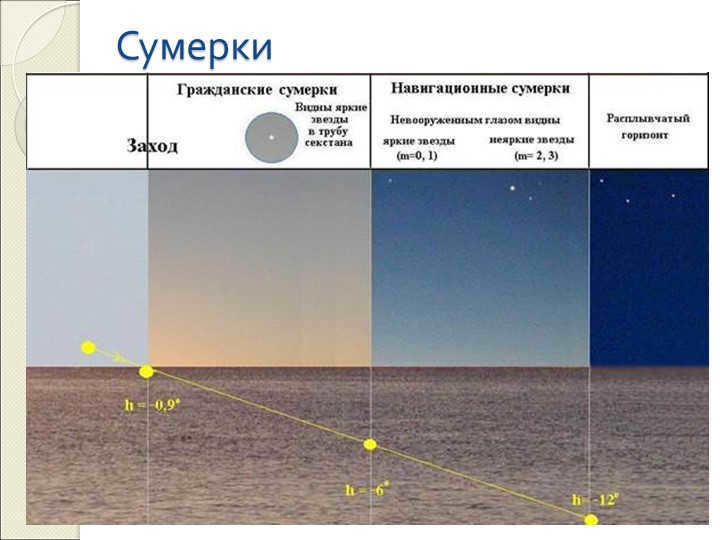
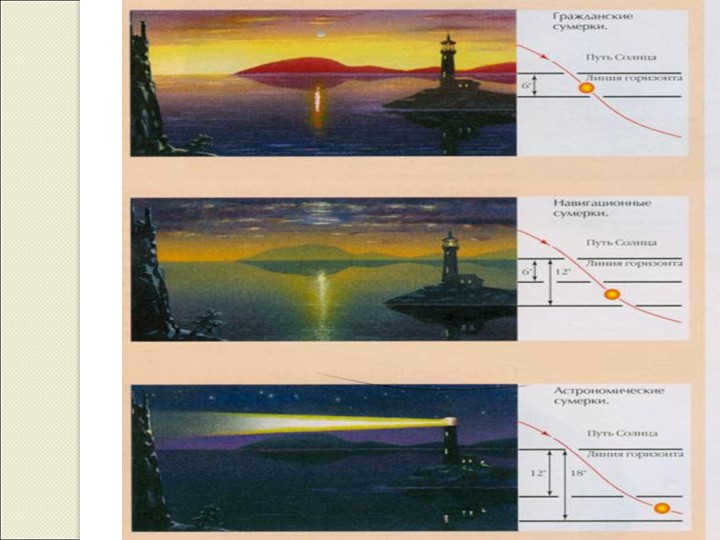
There are 25 slides dedicated to Twilight.
In the civil twilight phase, the Sun has gone 6º below the horizon. During this time, a person can see as well as they can during the day and there is no need for artificial light.
During the navigational twilight phase, which occurs from 6º to 12º, it becomes more difficult to read and the visibility of surrounding objects is significantly impaired. However, the ship’s navigator can still navigate by using the silhouettes of unlit shores.
The astronomical twilight phase occurs from 12º to 18º. During this time, it becomes completely dark, but the dim light of dawn still prevents the observation of faint stars.

Slide 29: Refraction – the bending of light rays in the Earth’s atmosphere
The apparent height of the celestial object is always greater than its actual height
Sunset. In reality, the Sun has already dipped below the horizon a few minutes ago.
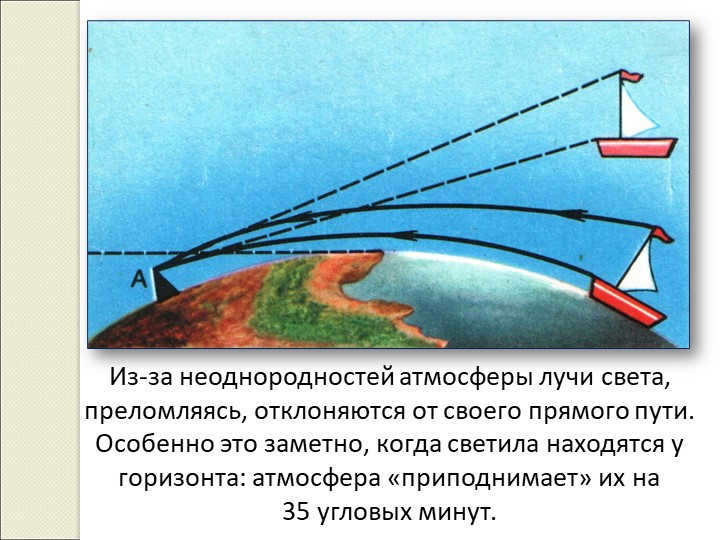

There is a phenomenon where light rays, refracting, get deflected from their original trajectory because of the irregularities present in the atmosphere. This effect becomes particularly noticeable when celestial objects are close to the horizon, as the atmosphere “lifts” them by approximately 35 angular minutes.
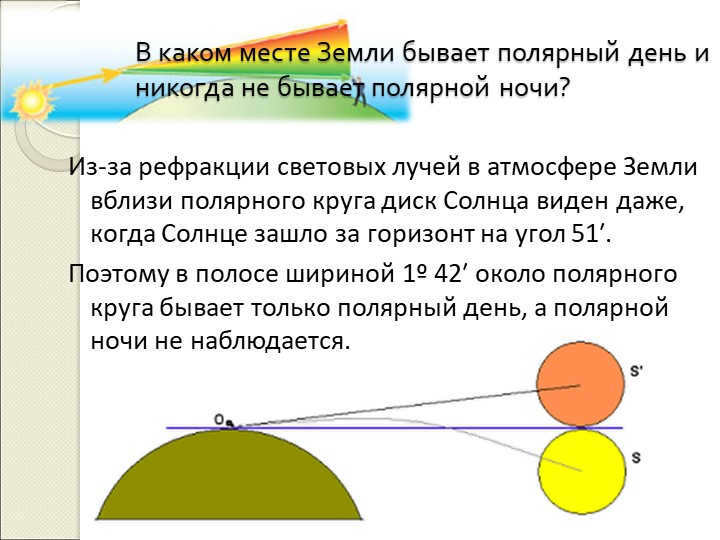
31 Slide Where on Earth can you find a place that experiences a polar day but never a polar night?
Because of the way light is refracted in the Earth’s atmosphere near the polar circle, the Sun’s disk remains visible even when it has dipped below the horizon at an angle of 51 minutes.
As a result, there is a narrow strip, approximately 1 degree and 42 minutes wide, near the Arctic Circle where the polar day is continuous and the polar night never occurs.

32 slide White Nights
During the pensive nights of yours.
Twilight that is transparent,
A gleam without the moon,
When I find myself in my room
Writing, reading with no need for a lamp,
And the sleeping ships are visible
on the empty streets,
And the Admiralty needle shines bright,
And, preventing the darkness of the night,
To the golden skies above,
One morning after another
Rushes, granting the night half an hour.
A.S. Pushkin. "The Bronze Horseman."


White Nights, also known as bright nights, occur during the early summer season. During this time, the evening dawn combines with the morning dawn, resulting in a continuous period of civil twilight throughout the night. This phenomenon can be observed in both the northern and southern hemispheres, specifically at latitudes exceeding 60 degrees. To classify as a White Night, the center of the Sun at midnight must dip below the horizon by no more than 7 degrees.

Slide 34: The tropical year is responsible for the Earth’s seasonal changes.
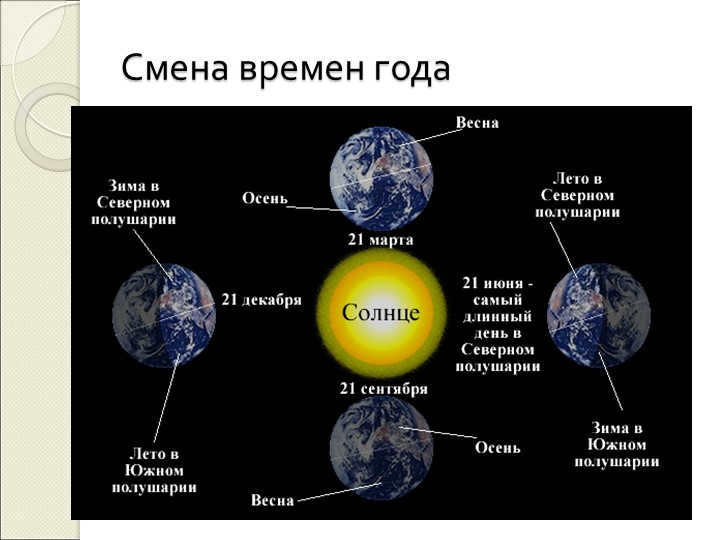
In the northern hemisphere of the Earth, summer occurs when the Sun illuminates the Earth’s north pole while the south pole is in shadow.
Conversely, winter occurs in the southern hemisphere.
When it is spring in the northern hemisphere, it is autumn in the southern hemisphere.
When it is autumn in the northern hemisphere, it is spring in the southern hemisphere.
The seasons in the northern and southern hemispheres are always opposite.
Slide 36: Climate – Tilt
The angle of the Earth’s axis of rotation is about 66°33′ tilted to the plane of the Earth’s orbit.
This tilt is responsible for the changing seasons.
It is caused by the Earth’s motion around the Sun and the tilt of its axis of rotation with respect to the plane of its orbit.
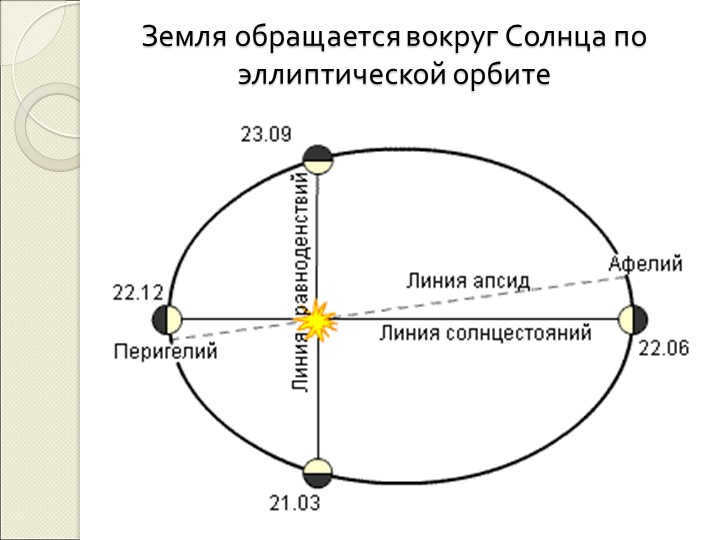

39 slide What is the difference in length between summer and winter?
The Earth’s speed as it orbits around the sun is not consistent, but it changes from 29.5 km/s in July (aphelion) to 30.3 km/s in January (perihelion).
The duration of the Earth’s orbit from fall to spring equinox is shorter compared to the summer section, and spring and summer in the Northern Hemisphere are 6 days longer than fall and winter.
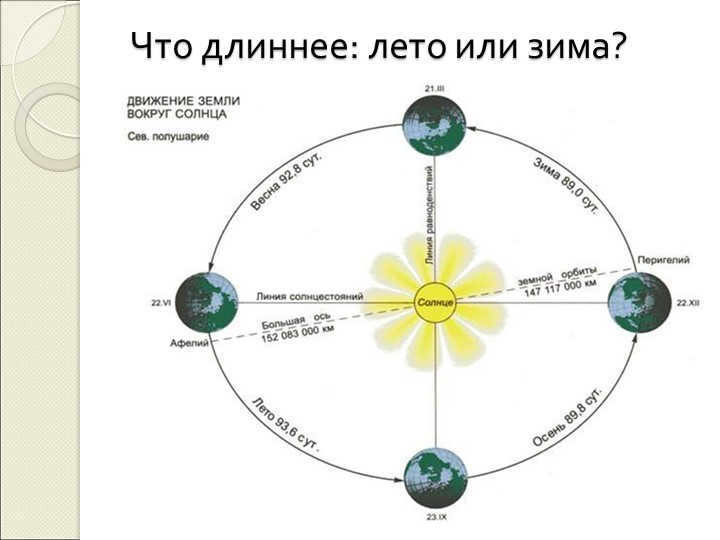

Slide 41: Which hemisphere of the Earth experiences higher temperatures: the northern or southern hemisphere?
The amount of solar energy reaching the Earth is inversely proportional to the square of the distance.
As a result, winters in the southern hemisphere are more severe than those in the northern hemisphere, while summers in the northern hemisphere are milder.
However, summers in the Northern Hemisphere are longer compared to winters.
Consequently, the Northern Hemisphere of the Earth tends to be warmer than the Southern Hemisphere.


Slide 42 The daily path of the Sun
This is a small circle on the celestial sphere that runs parallel to the celestial equator.
Throughout the year, the Sun moves both north and south in relation to the celestial equator.
However, the length of the day and night parts of its path are not equal.
They are only equal during the equinoxes, when the Sun is positioned directly on the celestial equator.
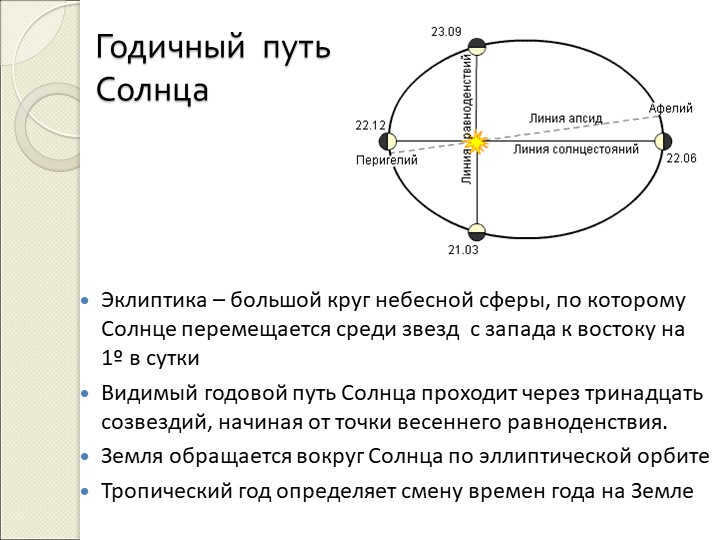

43 slide The Sun completes its yearly journey along the ecliptic, which is the circular path it follows across the celestial sphere. This path takes the Sun from west to east at a rate of 1 degree per day.
The visible annual path of the Sun passes through thirteen constellations, starting from the point of the vernal equinox.
The Earth travels around the Sun in an elliptical orbit, which determines the length of the tropical year and ultimately leads to the changing of seasons on Earth.

44 slide Literature
Vorontsov – Veliaminov B.A. Astronomy, 11 kl.: Textbook for general educational institutions / B.A. Vorontsov – Veliaminov, E.K. Straut, – M.: Drofa, 2017.
Ivanov A.A., Ivanova Z.I. Tests on astronomy, – Saratov: "Lyceum", 2002
Popova A.P., Popova O.A. Library of the teacher of astronomy. – Chelyabinsk: Academy of New Technologies, 2002.
"Open Astronomy 2.6" LLC "Physikon", 2005.
Encyclopedia for children. Т. 8 Astronomy. – 2nd edition, revised. Editor-in-chief M.D. Aksenova. – Moscow: Avanta+, 1999.
The topic of the lesson is “The annual movement of the Sun across the sky”.
The presentation provides both theoretical information and practical exercises.
The exercises involve using a dynamic star map, filling in a table, and then verifying the answers with the provided solution. The content is based on the latitude of the city of Miass (regional component).
- Evidence for portfolio
- Get eternal access for only 99 rubles
- Over 3,800 video lectures available for everyone
- Culmination (astronomy) refers to the moment when the center of a celestial body passes through the celestial meridian during its daily movement. It can also be described as the moment when the center of a celestial body intersects with the daily parallel of the luminary and the celestial meridian.
In the course of a day, all celestial bodies cross the celestial meridian twice. These crossings are known as the upper and lower culmination of the luminary. The upper culmination is when the luminary reaches its highest point, while the lower culmination is when it reaches its lowest point. For celestial bodies that do not set, both culminations occur above the horizon. For ascending and descending celestial bodies, the upper culmination happens above the horizon and the lower culmination occurs below the horizon. For celestial bodies that do not ascend, both culminations happen below the horizon and cannot be observed.
Additionally, differentiate between the upper culmination in the northern and southern regions of the zenith. In the event that the celestial body culminates to the south of the zenith, its astronomical azimuth at the moment of culmination is 0°, and if it culminates to the north, its azimuth at the moment of culmination is 180°.
By knowing the declination of the celestial body δ and the latitude of the observation location φ, we can calculate the zenith distances of the celestial body at the moments of culmination:
Nv; c.z = δ – φ. Similarly, by observing any star at the upper and lower culminations, we can determine its declination and the latitude of the observation location. If the upper culmination of a star occurs to the south of the zenith, then
φ = 90° – (hn-hv; s.w)/2; and if it occurs to the north of the zenith, then
Related ideas
The Celestial Pole is a point on the celestial sphere where the visible daily movement of stars occurs because of the Earth’s rotation on its axis. The direction to the North Celestial Pole coincides with the direction to the geographic north, while the direction to the South Celestial Pole coincides with the direction to the geographic south. The North Celestial Pole is located in the constellation Ursa Minor with the star Polaris, while the South Celestial Pole is located in the constellation Octans. Due to the Earth’s axis precession, the celestial poles shift about 20 arcseconds per year.
Solar days refer to the duration in which a celestial object completes one full rotation around its axis in relation to the Sun’s center. To be more precise, it represents the time span between two consecutive upper or lower culminations when the Sun’s center passes through the meridian at a specific location on Earth (or any other celestial body).
A celestial luminary is a term used to describe an astronomical entity that emits its own light or reflects light. It is also known as a “celestial body”. In the field of spherical astronomy, a celestial luminary can be interpreted as the projection of an astronomical object onto the celestial sphere. Celestial luminaries include the Sun, stars, the Moon, planets, their satellites, asteroids, comets, and other celestial bodies. In works of fiction, these names are often used to describe other planets, with “suns” being referred to.
The movements of the Sun and planets on the celestial sphere are a reflection of their visible movements, which are apparent to observers on Earth. Therefore, any movements of celestial bodies on the celestial sphere are not connected to the Earth’s daily rotation, as this rotation is represented by the rotation of the celestial sphere itself.
References in literature
In literature, there are often references to the consistent culmination of stars at the same altitude above the horizon in a particular locality. This phenomenon occurs because the angular distance of each star from the world pole and the celestial equator remains constant. However, it should be noted that this does not apply to the Sun or the Moon, as their culminations always differ in height. In fact, the interval between the climaxes of the Sun is 4 minutes longer than the interval between the climaxes of the stars. This discrepancy occurs because the Sun shifts in relation to the stars and the East by approximately 1 degree for every revolution of the celestial sphere, which takes 24 hours. Simple arithmetic calculations reveal that this shift amounts to 15 degrees per hour and 1 degree per 4 minutes. Additionally, the Moon culminates 50 minutes late due to its monthly revolution in sync with the rotation of the sky.
2 If you observe Orion for an extended period of time, you will notice a gradual rise and fall of the constellation. This pattern is also observed in almost all other stars, as they rise in the east, reach their highest point – culmination, and then set in the west, similar to the movement of the Sun.
In the distant future, a cosmic storm of epic proportions will reach its peak. Rocks and even tiny grains of sand will be propelled towards Earth. For a duration of one to two million years, the planet will experience an unprecedented influx of meteorites. The atmosphere will become enveloped in a dense cloud of dust. The impact of this event on Earth’s climate is still being studied by scientists, but it is likely that global cooling will occur. Certain regions may transform into barren deserts.
Continuation of Related Concepts
Stellar days refer to the duration of a celestial object’s rotation on its own axis in an inertial frame of reference, typically measured relative to distant stars. On Earth, it represents the time it takes for the planet to complete one full revolution around its axis in relation to these distant stars.
Sunrise is the specific moment when the upper edge of a celestial body becomes visible above the horizon. This term can also encompass the entire process of the visible disk of the celestial body crossing the horizon.
Astronomical refraction, also known as atmospheric refraction, describes the bending of light rays from celestial bodies as they pass through the Earth’s atmosphere, resulting in a shift in their apparent position in the sky.
An equinox is an astronomical event that occurs when the center of the Sun, in its apparent movement along the ecliptic, crosses the celestial equator.
The length of the day is the period of time between sunrise and sunset, during which at least part of the sun’s disk is visible above the horizon.
The ecliptic coordinate system, also known as ecliptic coordinates, is a celestial coordinate system in which the primary plane is the ecliptic plane and the pole is the pole of the ecliptic. It is used to observe the motion of celestial bodies in the solar system, many of which have orbital planes close to the ecliptic plane. It is also used to observe the apparent movement of the Sun across the sky throughout the year.
The geographic pole is the intersection point between the Earth’s surface and its axis of rotation. There are two geographic poles: the North Pole, which is located in the Arctic region of the Arctic Ocean, and the South Pole, which is located in Antarctica.
The progression of the equinoxes, known as praecessio aequinoctiorum in Latin, refers to the gradual movement of the vernal and autumnal equinox points. These points are where the celestial equator intersects with the ecliptic, and they shift slightly each year in accordance with the apparent annual motion of the Sun. In simpler terms, the vernal equinox occurs slightly earlier each year, approximately 20 minutes and 24 seconds earlier. In angular units, the offset is currently about 50.3″ per year, or 1 degree every 71.6 years. This is the offset between the equinox points.
The system of celestial coordinates known as the horizontal coordinate system, or horizon coordinate system, is characterized by its main plane being the mathematical horizon and its poles being the zenith and nadir. This particular system is utilized when observing stars and the movements of celestial bodies within the solar system from a ground-based perspective, whether it be with the naked eye, binoculars, or a telescope set to a specific azimuth of 85 degrees. It is important to note that the horizontal coordinates of not only the planets and the Sun, but also the stars, undergo constant changes throughout the day as a result of the Earth’s diurnal rotation.
Declination (δ) is one of the two coordinates in the equatorial coordinate system used in astronomy. It measures the angular distance on the celestial sphere from the plane of the celestial equator to the luminary and is typically expressed in degrees, minutes, and seconds of arc. The declination is positive north of the celestial equator and negative south of it.
The celestial equator is a large circle on the celestial sphere that is perpendicular to the axis of the Earth and coincides with the plane of the Earth’s equator. It divides the celestial sphere into two hemispheres: the northern hemisphere, centered on the north pole of the Earth, and the southern hemisphere, centered on the south pole of the Earth. The constellations that the celestial equator passes through are known as equatorial constellations.
A unique perspective on the cosmos – Gazing out into the vast expanse of space from the surface of a celestial body other than our own planet, Earth. This awe-inspiring view can differ greatly from what we observe from our home planet, and there are numerous reasons for this disparity. One of the most influential factors is the composition of the atmosphere surrounding the celestial body. Its density and chemical makeup play a significant role in determining the color of the sky. Additionally, the presence or absence of clouds can also impact the visual experience, with the potential for their colors to vary. Furthermore, the celestial objects visible from the surface, such as stars, satellites, planets, and even rings, can further contribute to the unique extraterrestrial heavens.
The celestial coordinate system is utilized in astronomy for the purpose of delineating the location of celestial objects in the expanse of the sky or specific points on an imaginary celestial sphere. These celestial objects or points are designated by two angular measurements, or arcs, that distinctly establish the position of objects on the celestial sphere. Consequently, the celestial coordinate system is classified as a spherical coordinate system in which the third coordinate, distance, is frequently unknown and does not exert any influence.
An eclipse refers to an astronomical phenomenon wherein one celestial body obstructs the light emitted by another celestial body.
A super moon is a celestial event that occurs when a full or new moon coincides with perigee, the point of closest approach between the Moon and the Earth. This occurs because the Moon follows an elliptical orbit around our planet. As a result of this phenomenon, observers on Earth are able to see a larger size of the lunar disk than usual.
Planetary retrograde motion refers to the observed backward motion of planets against the backdrop of stars on the celestial sphere. This motion appears to be from east to west, opposite to the regular motion of the Sun (annual) and the Moon.
The equation of time represents the discrepancy between mean solar time (MST) and true solar time (TST), which can be expressed as UV = MST – TST. This disparity remains constant for any observer at any location on Earth. To determine the equation of time, one can refer to specialized astronomical publications, utilize astronomical software, or employ the following formula.
Ecliptic (derived from the Latin term (linea) ecliptica, originating from the Greek word ἔκλειψις – eclipse) refers to a large circular path on the celestial sphere, tracing the annual apparent movement of the Sun. Consequently, the ecliptic plane corresponds to the plane of Earth’s revolution around the Sun (Earth’s orbit). A more precise contemporary definition of the ecliptic denotes it as the intersection of the celestial sphere with the orbital plane of the Earth-Moon barycenter.
Universal Time or UT (Universal Time) is a time scale that is based on the rotation of the Earth. Universal Time serves as a modern replacement for Greenwich Mean Time (GMT), which is sometimes mistakenly used as a synonym for Coordinated Universal Time (UTC). Universal Time was officially established on January 1, 1925. In reality, the term “world time” has multiple meanings, as there are various versions of world time, with the main ones being UT1 and UTC (as described below).
The Terminator (derived from the Latin word “terminare” meaning “to cease”) is a boundary line that separates the illuminated (light) portion of a celestial body (such as a planet or moon) from the unilluminated (dark) portion. The terminator of a spherical body is always observed in the shape of a semi-ellipse, which appears as a straight line at the end of the first quarter and the beginning of the last quarter.
Conjunction (in the field of astronomy) refers to the alignment of celestial objects where their ecliptic longitudes are identical. In some cases, the concept of conjunction based on direct ascent rather than ecliptic longitude is also considered. As a result, during a conjunction event, two celestial bodies are relatively close to each other on the celestial sphere (although the exact moment of conjunction may not necessarily coincide with the moment of closest approach). The term conjunction is also commonly used in astrology.
Radiant (derived from Latin “radians” and genitive “radiantis” meaning radiating) describes a specific region of the celestial sphere that appears to be the source of meteors. These meteors become visible when the Earth encounters a swarm of meteoric bodies that orbit the Sun in a shared trajectory.
The horizon, derived from the Greek word ὁρίζων meaning “limiting,” refers to the boundary where the sky meets the surface of the earth or water. It can also encompass the visible portion of this surface. There exists a distinction between the visible horizon and the true horizon. The angle between the plane of the true horizon and the direction towards the visible horizon is known as the horizon inclination, which can also be referred to as horizon depression.
The starry sky consists of a collection of celestial bodies that are visible during the nighttime. These celestial bodies are primarily stars. With the naked eye, one can typically discern stars up to the 5th or 6th magnitude. In optimal observing conditions, such as a cloudless sky, it is possible to see up to 800 stars with a magnitude of up to 5, and up to 2.5 thousand stars with a magnitude of up to 6. Many of these stars are situated near the Milky Way band. It is worth noting that the total number of stars within our Galaxy alone surpasses this count.
The celestial body’s opposition is a position in the solar system where its ecliptic longitude differs by 180 degrees from the Sun. This means that the body is located along the line “Sun – Earth” and is visible from the Earth in the opposite direction of the Sun. Opposition can only occur for planets and other bodies that are farther from the Sun than the Earth.
In the field of astronomical navigation, there are fifty-eight special navigational stars. These stars are among the brightest out of the approximately 6000 stars visible to the naked eye under optimal conditions. They span across 38 constellations on the celestial sphere, ranging from declination -70 degrees to +89 degrees. Many of these navigational stars were named by ancient civilizations such as the Babylonians, Greeks, Romans, and Arabs.
The point where the perpendicular to the ecliptic plane intersects the celestial sphere is known as the pole of the ecliptic. This serves as the pole for the ecliptic celestial coordinate system.
Right ascension (abbreviated as α or R. A.) measures the arc length along the celestial equator from the vernal equinox to the declination circle of a celestial object. It is one of the coordinates in the equatorial coordinate system, which has two coordinates – the other being declination.
The phase of the Moon known as the first quarter, or Luna crescens dimidiata in Latin, occurs when exactly half of the visible part of the Moon is illuminated. Unlike the last quarter, the proportion of the illuminated part is increasing during this phase as the Moon progresses from new moon to full moon. During the first quarter, the Moon is in the eastern quadrature, meaning it is at an angular distance of 90° from the Sun. It is positioned east of the Sun, resulting in the western side of the Moon’s visible surface being illuminated.
In astronomy, an epoch (from the Greek έποχή meaning “stop”) refers to a specific moment in time for which astronomical coordinates or orbital elements are defined. Astronomical coordinates can be recalculated from one epoch to another, taking into account factors such as precession and proper motion.
The summer solstice occurs when the Earth’s axis is tilted towards the Sun at its lowest point.
Mercury’s transit across the Sun is an astronomical event where Mercury moves directly between the Sun and the observer (Earth, spacecraft, etc.). When viewed from Earth or nearby, Mercury appears as a small black dot crossing the solar disk.
The parade of planets is an astronomical phenomenon where multiple planets in the solar system align on one side of the Sun within a small section. During this alignment, the planets are relatively close to each other in the celestial sphere.
Solstice (also known as solstovorót in Old Russian) is an astronomical occurrence that marks the highest and lowest positions of the Sun in relation to the celestial equator during its annual movement along the ecliptic.
The zenith is the point on the celestial sphere that is directly above the observer’s head. It can also be defined as the direction that points directly upwards from a specific location, which is one of the two vertical directions that are perpendicular to the horizontal plane at the observer’s position. In the fields of astronomy, geophysics, and other related sciences such as meteorology, the concept of “up” is more accurately defined as the direction that is opposite to the gravitational force at a given location.
Moon phases are cyclic changes in the appearance of the illuminated portion of the Moon in the Earth’s sky. The phases of the Moon gradually and periodically shift during the synodic month (approximately 29.5306 average solar days), as well as due to the Moon’s orbital position as it orbits around the Earth and the Earth orbits around the Sun.
Analemma (from the Greek word “ανάλημμα”, meaning “basis, foundation”) – is a curve that connects a series of consecutive positions of the central star of a planetary system (in our case, the Sun) in the sky of one of the planets in this system at the same time of day throughout the year.
Sunset, or sundown, is the moment when the upper edge of the Sun disappears below the horizon. The term sunset can also refer to the entire process of the Sun’s visible disk crossing the horizon.
The Synodic Circumference Period (derived from the Greek word σύνοδος – conjunction) refers to the time interval between two consecutive conjunctions of the Moon or any planet in the solar system with the Sun, as observed from Earth. Notably, the conjunctions of the planets with the Sun must occur in a specific linear order, which is particularly important for the inner planets. For instance, this can involve consecutive upper conjunctions, where a planet passes behind the Sun.
Both the Moon and the other planets cross the celestial meridian twice in a day during their apparent motion. The crossing of the celestial meridian by the center of the celestial body is known as its culmination. The term “culmination” originates from the Latin word, and it signifies the top or highest point. It is worth noting that there is a distinction between the upper and lower culminations of the celestial body.
Fig. 1.23. Culmination of celestial bodies: a – south of the zenith; b – north of the zenith.
The luminary reaches its greatest height during the upper culmination and its lowest height during the lower culmination. In the case of luminaries that do not rise, both climaxes occur above the horizon. However, for luminaries that rise and set, the upper culmination happens above the horizon while the lower culmination occurs below it. In the case of luminaries that do not rise, both climaxes happen below the horizon and cannot be observed.
The highest point of the celestial body can be observed between the zenith and the southern point (located on the southern part of the meridian) or between the zenith and the celestial pole (located on the northern part of the meridian). Figure 1.23 depicts the celestial sphere. The main circles are represented by diameters and chords. The figure illustrates that luminaries with a declination less than the latitude of the place culminate south of the zenith, while those with a declination greater than the latitude of the place culminate north of the zenith.
During the upper culmination, the hour angle of the celestial body is 0, and during the lower culmination, it is 180 degrees. The azimuth of the celestial body during the upper culmination is 0 degrees north of the zenith and 180 degrees south of the zenith.
When the luminary reaches its highest point in the southern part of the sky, the altitudes at the time of its highest and lowest points are calculated using the following formulas:
When the luminary reaches its highest point in the northern part of the sky, the altitudes at the time of its highest and lowest points are calculated using the following formulas:
By generalizing the formulas for calculating the luminary’s altitude at its highest point, we find that the plus sign is used when the luminary culminates in the southern part of the sky, and the minus sign is used when it culminates in the northern part of the sky.
The altitude at the time of the luminary’s lowest point is determined using the same formula for all luminaries.
By analyzing the given equations, it becomes evident that at extreme values of the Sun’s declination, when it reaches its highest point during upper culmination, the Sun will be directly overhead at geographic latitudes of 90°. This means that the Sun will be at its zenith. This occurs on a geographic parallel with a northern latitude of [insert value]. On the summer solstice, the Sun reaches its zenith on this parallel. Conversely, on the winter solstice, the Sun reaches its zenith on a geographic parallel with a southern latitude of [insert value]. The geographic parallel with a northern latitude of [insert value] is known as the northern tropic, or the tropic of Cancer. Similarly, the geographic parallel with a southern latitude of [insert value] is known as the southern tropic, or the tropic of Capricorn. Many centuries ago, these constellations marked the points of solstices.
According to formulas, it can be observed that when the Sun is at its highest point in the sky, its height is zero on latitudes. On a specific geographical parallel, the Sun’s height is zero at the moment of its lowest point on the day of the summer solstice and at the moment of its highest point on the day of the winter solstice. In other words, on this parallel, the Sun neither sets nor rises on these days. This geographical parallel is known as the Arctic Circle.
On another geographical parallel, the Sun does not set on the day of the winter solstice and does not rise on the day of the summer solstice. This parallel is called the South Polar Circle.
Example 1. Find the altitude of star Deneb when it reaches its highest and lowest points in the sky, based on the latitude of the observer’s location.
Solution 1. Calculate the star’s position relative to the zenith at the moment of its highest point. Since Deneb culminates north of the zenith, its altitude will be above the observer’s horizon.
2. Determine the star’s altitude at its highest point:
3. Determine the star’s altitude at its lowest point: . Due to the latitude of the observer, Deneb will rise and set, resulting in different altitudes at its highest and lowest points in the sky.
Example 2. On June 22nd, with the Sun’s declination and the latitude of Leningrad, calculate the Sun’s altitude at its highest and lowest points in the sky.
Solution 1. Calculate the Sun’s position in relation to the zenith during its upper culmination. At this time, the Sun is located south of the zenith.
2. Determine the Sun’s elevation during its upper culmination.
3. Determine the Sun’s elevation during its lower culmination.
Based on the given example, we can observe that in Leningrad, at the latitude specified, on the day of the summer solstice, the Sun does not fall below the horizon by more than 6 degrees. This means that during summer in Leningrad, there is almost no complete darkness at night, as twilight persists.
Example 3. Star Vega; the star’s declination corresponds to the latitude of the observer’s location. Calculate the star’s altitude during its upper and lower culminations.
Approach. 1. Establish the star’s position in relation to the zenith during its upper culmination. As the star’s declination is lower than the latitude of the observer’s location, the star reaches its highest point to the south of the zenith.
2. Calculate the star’s elevation during its upper culmination: .
3. Determine the star’s altitude during its lower culmination: .
At this latitude, the star Vega remains above the horizon throughout its upper and lower culminations, making it a perennially visible star.


Lexicon of cosmic terms
Achievements of celestial bodies (derived from the Latin word culminis – the highest point)
The point at which a celestial body crosses the celestial meridian in the southern part of the sky, indicating its highest position above the horizon, is referred to as the upper culmination. When non-setting celestial bodies cross the celestial meridian in the northern part of the sky, it is known as the lower culmination. These terms are applicable to the northern hemisphere of the Earth. In the southern hemisphere, the upper culmination takes place in the northern part of the sky, while the lower culmination occurs in the southern part.
Text excerpt containing an error:
If you come across an error in the text, please notify us by selecting the erroneous part and pressing the “Ctrl+Enter” key combination.
Let’s proceed with the discussion regarding the apex of the luminaries. The fundamental principles can be found in the initial article on culminations.
The superior culmination is located to the south of the zenith
As previously mentioned, the elevation of the world pole above the horizon is equivalent to the latitude of the observation location. NS represents the plane of the mathematical horizon, PP’ represents the world axis, and P denotes the north pole of the world. This implies that
where φ represents the latitude of the observation location. Hence,
∠NOQ’ = β = 90° – φ = ∠SOQ (as vertical).
Given that QQ’ is the celestial equator and KK’ is the diurnal parallel of the luminary, then
Our objective is to determine the relationship between the luminary’s altitude above the horizon at the moment of its upper culmination south of the zenith, and the latitude of the observation location and declination. Therefore, we are interested in
The height of the celestial body above the horizon during its highest point in the southern part of the sky can be calculated using the formula: h = 90° – φ + δ
When the celestial body reaches its highest point in the northern part of the sky, it is called the upper culmination north of the zenith.
After analyzing the data from our previous findings, we have come to understand that
∠NOK, which represents the altitude of the luminary above the horizon during its upper culmination north of the zenith, can be calculated using the formula ∠NOK = h = ∠POK + ∠NOP = 90° – δ + φ
This formula helps us determine the luminary’s height above the horizon at the moment of its upper culmination north of the zenith, where h = 90° – δ + φ
For the lower culmination north of the nadir
The altitude of the celestial body above the horizon when it reaches its lowest point in the southern direction from the nadir can be calculated using the formula:
h = φ + δ – 90°
Lower culmination in the opposite direction from the nadir
It is crucial to understand that the luminary’s declination is negative and the altitude should be negative as well.
However, due to the negative declination and the necessary negative altitude, ∠K’OP’ equals -90° – δ.
Furthermore, considering the negative altitude requirement, ∠K’OS equals -90° – δ – φ.
The luminary’s altitude above the horizon during the time of the lower culmination south of the nadir can be calculated as follows: h = -φ – δ – 90°.
PS is an elevated pole, specifically the south pole, while line NS represents the observer’s horizon. ZZ’ represents the plumb line, and QQ’ represents the equator. Line AA’ is the diurnal parallel of the luminary. The angle φ represents the latitude of the observer’s location, δ represents the declination of the luminary, z↑ represents the zenith distance at the upper culmination, and z↓ represents the zenith distance at the lower culmination.
In astronomy, culmination refers to the passage of the center of the luminary through the celestial meridian during its daily movement. Alternatively, it can refer to the passage of the luminary’s center through the point where the daily parallel of the luminary intersects with the celestial meridian.
Throughout the course of the day, all celestial bodies cross the celestial meridian twice. The upper and lower culminations of the celestial body are distinguished. Assuming that the declination of the celestial body remains constant during the day, the height of the celestial body is highest during its upper culmination and lowest during its lower culmination. For celestial bodies that do not rise, both culminations occur above the horizon. For celestial bodies that rise and set, the upper culmination occurs above the horizon while the lower culmination occurs below the horizon. In the case of celestial bodies that do not erupt, both culminations occur below the horizon and cannot be observed [1].
Additionally, differentiate between the northern and southern upper culminations of the zenith. When a celestial body reaches its highest point south of the zenith, its astronomical azimuth is 0° at that moment. Conversely, when a celestial body reaches its highest point north of the zenith, its azimuth at the moment of culmination is 180°.
Just as the positive values of northern geographic latitude and northern declination, and the negative values of southern declination, can be assigned a sign and zenith distance. A convenient rule to use is that if the shadow of the observer (whether real or imaginary) of the luminary falls in the north, the zenith distance of the luminary is positive, and if it falls in the south, the zenith distance is negative. The same rule can be derived from considering the astronomical azimuth of the luminary: when the luminary is at its highest point south of the zenith, its astronomical azimuth is 0°, and cos(0°) = +1; when the luminary is at its highest point north of the zenith, the azimuth is 180°, and cos(180°) = -1. Algebraically, the sign of the zenith distances can be determined by calculations that observe the conventions of the signs of latitude and declination.
By measuring the highest points of stars on opposite sides of the zenith at similar zenith distances, it is possible to calculate latitude. To do this, it is important to have knowledge of the declination of both stars, which significantly improves the accuracy of the measurement. This technique is referred to as the Talcott method. If the Polaris, also known as the north star, is at its highest point, the formula to be used is as follows [2]:
If the Polaris is at its lowest point, the formula would be:

The movement of the planets affects our lives in many ways, including the way we measure time. In this lesson, we will explore how to calculate the precise time for any location on Earth. We will discover the connection between solar days and geographic meridians, and learn about the international date line and its location. Additionally, we will examine different calendar systems and the principles on which they are based.

Currently, it is not possible for you to view or share the video lesson with your students
In order to access this lesson and other video lessons in the package, you will need to add it to your individual account.
Unlock amazing possibilities

Outline of the Lesson “Time and the Calendar”
Our entire existence is intertwined with time and regulated by the recurring transitions between day and night and the changing seasons. It is a well-known fact that the Sun only lights up half of the Earth at any given time, resulting in daytime on one hemisphere and nighttime on the other. As a result, there are constantly locations on our planet where it is noon and the Sun is at its highest point, as well as places where it is midnight and the Sun is at its lowest point in the sky.
The point at which the center of the Sun reaches its highest point in the sky is known as true noon, while the point at which it reaches its lowest point is known as true midnight. The duration between two consecutive occurrences of these points is referred to as a true solar day.
It appears that they have the potential to accurately measure time. However, due to the Earth’s elliptical orbit, solar days experience periodic variations in their duration. When the Earth is nearest to the Sun, it travels at a speed of approximately 30.3 km/s. Conversely, after six months, when the Earth is farthest from the Sun, its speed decreases by 1 km/s. This irregular movement of the Earth in its orbit leads to an irregular apparent movement of the Sun across the celestial sphere. Essentially, at different times of the year, the Sun appears to “move” across the sky at varying speeds. As a result, the length of true solar days continuously changes, making them impractical for time measurement. Therefore, in everyday life, we rely on average solar days instead. These days are assumed to have a constant duration of 24 hours. Each hour of average solar time is further divided into 60 minutes, and each minute is divided into 60 seconds.
The measurement of time by solar day is associated with the geographical meridian. The time measured at a specific meridian is referred to as its local time, which is consistent for all points on it. However, the further eastward the meridian, the earlier the day begins. Taking into account that our planet rotates around its axis by 15° per hour, the time difference between two points in one hour corresponds to the difference in longitudes by 15°. Therefore, the local time at two points will differ exactly by the difference in their geographic longitude, expressed in hours:
T1 – T2 = λ1 – λ2.
As you have learned in your geography course, the starting meridian, also known as the zero meridian, is defined as the meridian that runs through the Greenwich Observatory in the vicinity of London. The average solar time at the Greenwich meridian is referred to as Universal Time (UT for short).

To determine the local time of any point, you can use the Universal Time and the geographic longitude:
T1 = UT + λ1.
This equation can also be used to find the geographic longitude based on the Universal Time and local time, which is determined through astronomical observations.
However, if we were to rely on local time in our daily lives, we would constantly need to adjust the clock as we travel east or west of our home location.
For example, let’s calculate the time difference between noon in St. Petersburg and Moscow, given their known geographic longitudes.

To put it differently, noon in St. Petersburg will be approximately 29 minutes and 12 seconds later than in Moscow.
The resulting inconvenience is so evident that nowadays virtually the entire global population utilizes the time zone system. It was proposed by an American educator named Charles Dowd in 1872 for implementation on the American railway system. In 1884, the International Meridian Conference took place in Washington, D.C., which led to the recommendation of utilizing Greenwich time as the worldwide standard.
Based on this system, the whole world is divided into 24 time zones, each of which spans 15 degrees of longitude (or one hour). The time zone of the Greenwich meridian is considered to be zero. The remaining zones, from zero to the east, are assigned numbers ranging from 1 to 23. Within each zone, at any given point in time, the time remains constant, while in adjacent zones it differs by exactly one hour.
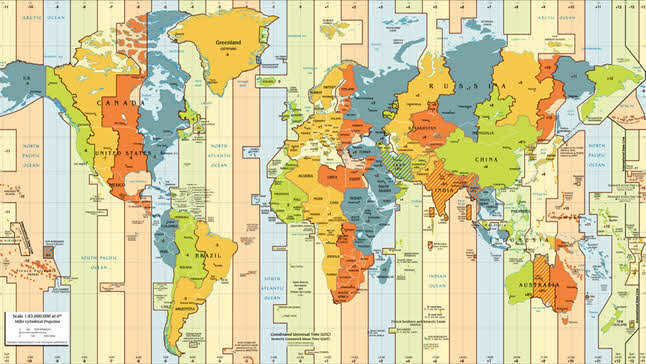
Therefore, the local time, which is observed in a specific location, differs from the world time by the number of hours that corresponds to its time zone:
T = WT + n.
If you examine the time zone map, you will easily notice that their boundaries coincide with meridians only in sparsely populated areas, such as seas and oceans. In other regions, for convenience, time zone boundaries are drawn along state and administrative borders, mountain ranges, rivers, and other natural divisions.
In the present day, atomic time is regarded as the most dependable and convenient form of timekeeping. Atomic time was established by the International Committee of Weights and Measures in 1964. Atomic clocks were adopted as the universal time standard, with an error rate of about one second in 50 thousand years. As a result, since January 1, 1972, countries around the world have been measuring time based on atomic clocks.
For the purpose of measuring long periods of time, the calendar was introduced, which establishes a certain duration of months, their order in the year, and the initial moment of counting years. This system is based on periodic astronomical phenomena, including the Earth’s rotation around its axis, the change of lunar phases, and the Earth’s revolution around the Sun. There are over 200 different calendar systems, each of which is based on three fundamental units of time measurement: the average solar day, the synodic month, and the tropical (or solar) year.
It is worth noting that the synodic month refers to the time interval between two consecutive identical phases of the Moon, which is approximately 29.5 days.
A tropical year is the period of time between two consecutive passages of the center of the Sun through the vernal equinox. On average, it lasts for 365 d 05 h 48 min 45.19 s since January 1, 2000.
As observed, both the synodic month and the tropical year do not consist of a whole number of average solar days. This discrepancy has led different cultures to create their own methods of harmonizing the day, month, and year. Consequently, various peoples have developed their own calendar systems throughout history. However, these calendars can generally be categorized into three types: lunar, luni-solar, and solar.

The lunar calendar is divided into 12 lunar months, each containing 30 or 29 days. This makes the lunar calendar about ten days shorter than the solar year. This type of calendar is widely used in the modern Islamic world.
Lunar-solar calendars are the most complex as they are based on the ratio that 19 solar years are equal to 235 lunar months. This means that a year can have either 12 or 13 months. The Jewish calendar currently follows this system.
The Julian calendar, named after Julius Caesar, was developed in ancient Rome on January 1, 45 B.C. It served as the immediate predecessor to the modern calendar.

The calendar known as the Julian calendar was based on the length of the tropical year, which was approximately 365.25 days. To make the calendar more convenient, it consisted of three years with 365 days each. In addition, every fourth year had an extra day added to February, making it a leap year.
However, the Julian calendar was not perfect. The length of the calendar year differed from the tropical year by 11 minutes and 14 seconds. This discrepancy became noticeable in the 16th century when it was observed that the day of the vernal equinox, which is important for church holidays, had shifted by 10 days.
To correct this accumulated error and prevent future shifts, Pope Gregory XIII reformed the calendar in 1582. The reform involved moving the count of days forward by 10 days.

Simultaneously, in order to align the average calendar year more accurately with the solar year, Gregory XIII implemented a modification to the rule of leap years. The leap year continued to be defined as a year whose number was a multiple of four, but an exception was made for years that were multiples of one hundred. These years would be leap years only if they were also divisible by 400. For instance, 1700, 1800, and 1900 were considered regular years, while 1600 and 2000 were considered leap years.
The adjusted calendar came to be known as the Gregorian calendar or the new style calendar.
In Russia, the new style calendar was not adopted until 1918. By that time, a difference of 13 days had accumulated between it and the old style calendar.






