Who classified the stars into six different magnitudes?

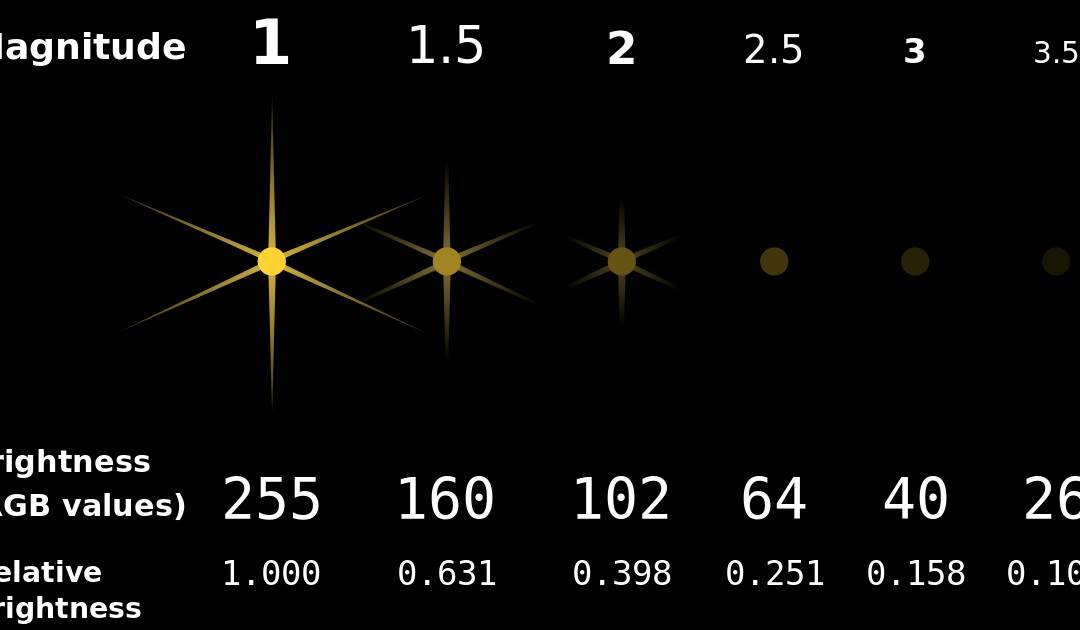
In astronomy, stellar magnitude is a unitless measurement used to quantify the brightness of an object within a specific range of wavelengths, typically in the visible or infrared spectrum but occasionally spanning all wavelengths. The concept of magnitude was initially introduced by Hipparchus in ancient times, although the definition was not precise.

The magnitude scale is logarithmic, meaning that each step in magnitude represents a specific change in brightness. Specifically, a one magnitude step corresponds to a 2.512-fold difference in brightness. For instance, a star with a magnitude of 1 is exactly 100 times brighter than a star with a magnitude of 6. The lower the magnitude value, the brighter the object, with the brightest objects having negative magnitude values.

There are two different ways that astronomers measure the brightness of stars: apparent stellar magnitude and absolute stellar magnitude. Apparent stellar magnitude (m) refers to how bright a star appears in the night sky from Earth. The apparent magnitude of a star is influenced by factors such as its intrinsic luminosity, distance from Earth, and any reduction in brightness caused by extinction. On the other hand, absolute stellar magnitude (M) describes the actual amount of light emitted by a star and is defined as the apparent magnitude that the star would have if it were located at a specific distance from Earth, which is 10 parsecs for stars. When it comes to planets and smaller objects within our solar system, a more complex definition of absolute stellar magnitude is used. This definition takes into account the brightness of these objects when they are observed from a distance of one astronomical unit from the observer and the Sun.

The Sun’s magnitude is -27, while Sirius, the brightest star in the night sky, has a magnitude of -1.46. Artificial objects in Earth’s orbit, such as the International Space Station (ISS), can also be assigned apparent magnitudes, with the ISS sometimes reaching -6.

• 1. History
• 1.1. Modern definition
• 3.1. Apparent stellar magnitude
• 3.2. Absolute stellar magnitude
• 3.3. Examples
• 3.4. Other scales

Historical Background

The concept of the magnitude system can be traced back to approximately 2000 years ago when the Roman poet Manilius introduced a classification system for stars based on their apparent brightness. Contrary to popular belief, it was Manilius and not the Greek astronomer Hipparchus or the Alexandrian astronomer Ptolemy who first devised this system (although there are varying references on this). The term “magnitude” was used to refer to the perceived size or dimension of stars. When observing stars with the naked eye, brighter stars like Sirius or Arcturus were seen as larger in size compared to less visible stars like Mizar, and even smaller in size compared to extremely faint stars like Alcor. In 1736, the mathematician John Keil provided a detailed description of this ancient magnitude system that was based on observations made without the aid of telescopes:

Keep in mind that the magnitude of a star decreases as it becomes brighter: stars that are classified as “first magnitude” are considered to be top-tier stars, whereas stars that are barely visible to the naked eye fall into the category of “sixth magnitude” or “6th star”. This classification system was a straightforward way of categorizing the brightness of stars into six distinct groups, but it failed to take into account any variations in brightness within each group.

Tycho Brahe made an effort to directly measure the angular size of stars, which implied that the magnitude of a star could be determined objectively rather than subjectively. He concluded that first-magnitude stars have an apparent diameter of 2 angular minutes (2 ′) (1/30 degrees, or 1/15 the diameter of a full moon), with second to sixth-magnitude stars measuring 1/2 ′, 1/12 ′, 1/4 ′, 1/2 ′, and 1/3 ′, respectively. However, the development of the telescope revealed that these sizes were misleading as the stars appeared much smaller through the telescope. Early telescopes produced a false disk-shaped image of the star, with the size of the disk being larger for brighter stars and smaller for fainter stars. Astronomers from Galileo to Jacques Cassini mistakenly believed that these false disks were the physical bodies of stars, leading them to associate magnitude with the physical size of a star. Johannes Hevelius compiled a highly accurate table of star sizes measured through a telescope, but the measured diameters ranged from just over six angular seconds for first magnitude to just under 2 seconds for sixth stellar magnitude. By the time of William Herschel, astronomers realized that the telescopic disks of stars were false and depended on the telescope as well as the brightness of the stars, but still provided some information about a star’s size. Even in the nineteenth century, the system of stellar magnitudes continued to be described in terms of six classes based on apparent size, in which

There are no set rules for classifying stars, as it ultimately depends on the observer’s estimation. As a result, some astronomers may consider certain stars to be of first magnitude, while others may classify them as second magnitude.

However, by the middle of the nineteenth century, astronomers were able to measure the distances to stars using stellar parallax. This led them to realize that stars were actually located so far away that they appeared as point sources of light. With further advancements in understanding light diffraction and astronomical vision, astronomers came to fully understand that the apparent sizes of stars are deceptive and dependent on the intensity of light emitted by the star. This apparent brightness of a star can be measured in units such as watts/cm, resulting in brighter stars appearing larger in size.

The contemporary interpretation

In the early days, scientists used photometric measurements to compare the brightness of stars. They achieved this by projecting a synthetic “star” into the telescope’s field of view and adjusting it to match the brightness of real stars. The results showed that stars of the first magnitude were approximately 100 times brighter than those of the sixth magnitude.

To standardize these measurements, Norman Pogson of Oxford proposed a logarithmic scale in 1856. He suggested that there should be a ratio of √100 ≈ 2.512 between each stellar magnitude, so that a difference of five magnitudes would equate to a difference of 100 in brightness. In other words, each increase of one magnitude signifies a change in brightness by a factor of √100, or about 2.512. Consequently, a star of 1st magnitude is roughly 2.5 times brighter than a star of 2nd magnitude, which is in turn 2.5 times brighter than a star of 3rd magnitude, and so on.

This is the contemporary system of stellar magnitude, which measures the luminosity, not the apparent size, of stars. Utilizing this logarithmic scale, a star can have a luminosity greater than “first class”, so Arcturus or Vega have a stellar magnitude of 0, and Sirius has a stellar magnitude of -1.46.

Scale

As previously stated, the scale functions in reverse when objects with a negative magnitude are brighter than objects with a positive magnitude. The more negative the value, the brighter the object.

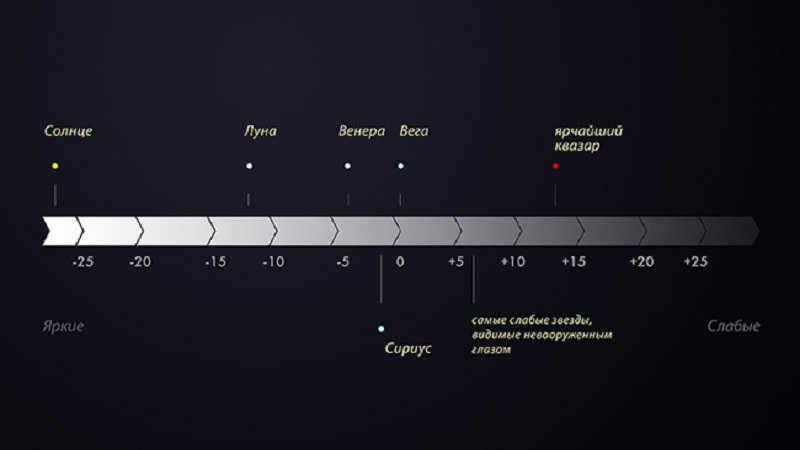
The line is divided into six magnitudes, with brighter objects located to the left and dimmer objects located to the right. The center of the line represents zero, while the far left side showcases the brightest objects and the far right side showcases the dimmest objects.

The astronomers focus on two main types of magnitudes:

• Apparent magnitude, which refers to the brightness of an object as it is observed in the night sky.
• Absolute magnitude, which is a measure of the luminosity of an object (or reflected light for non-luminous objects like asteroids); it represents the apparent magnitude of an object observed from a specific distance, typically 10 parsecs (32.6 light-years).

The distinction between these terms can be illustrated by comparing two stars. Betelgeuse (with an apparent magnitude of 0.5 and an absolute magnitude of -5.8) appears slightly dimmer in the sky compared to Alpha Centauri (with an apparent magnitude of 0.0 and an absolute magnitude of 4.4), despite the fact that Betelgeuse emits thousands of times more light due to its significantly greater distance.

Apparent magnitude

Within a contemporary logarithmic scale for magnitude, two objects, with one serving as a point of reference or baseline, and their brightnesses measured from Earth in units of power per unit area (e.g., watts per square meter, W – m) being denoted as I1 and Iref, will have magnitudes m1 and mref related through the equation:

m1 – mref = -2.5 log10(I1/Iref)

-m_ > = -2.5 \ log_ \ left (> > > \ right ).>

By utilizing this equation, the scale of stellar magnitude can be expanded beyond the traditional range of 1-6, transforming it into a precise indicator of brightness rather than merely a classification system. Presently, astronomers are capable of measuring magnitude variances down to one hundredth of a stellar magnitude. Stars with magnitudes falling between 1.5 and 2.5 are referred to as second magnitude, while there exist approximately 20 stars that are brighter than 1.5 and are thus classified as first magnitude stars (consult the list of brightest stars for more information). To provide some examples, Sirius possesses a stellar magnitude of -1.46, Arcturus boasts a magnitude of -0.04, Aldebaran displays a magnitude of 0.85, Spica exhibits a magnitude of 1.04, and Procyon manifests a magnitude of 0.34. According to the ancient system of stellar magnitudes, all of these stars would be classified as “first magnitude stars.”

It is also possible to calculate the stellar magnitude for objects that are much brighter than stars (such as the Sun and Moon), as well as for objects that are too faint for the human eye to see (like Pluto).

Stellar magnitude in absolute terms

Often referred to as apparent magnitude because it can be directly measured. The absolute stellar magnitude can be determined by using a formula that takes into account the apparent stellar magnitude and the distance:

This is known as the distance modulus, where d represents the distance to the star measured in parsecs, m is the apparent stellar magnitude, and M is the absolute stellar magnitude.

If the line of sight between the object and the observer is influenced by the absorption caused by interstellar dust particles, the brightness of the object will appear dimmer. When considering extinction magnitudes A, the relationship between apparent and absolute magnitudes can be described as follows:

Stellar absolute magnitudes are typically represented by the capital letter M with a lowercase letter denoting the bandwidth. For instance, M V refers to the magnitude at a distance of 10 parsecs in the V passband. A bolometric magnitude (M bol) is an absolute magnitude that takes into account emission across all wavelengths; it generally appears smaller (i.e., brighter) than the absolute magnitude in a specific passband, especially for objects that are very hot or very cold. Bolometric magnitudes are calculated based on stellar luminosities in watts and are normalized to be approximately equal to M V for yellow stars.

Illustrations

Displayed beneath is a chart showing the observable brightness of stars and man-made satellites, spanning from the Sun to the dimmest object that can be detected using the Hubble Space Telescope (HST):

Apparent magnitude.Brightness. relative to. magnitude 0Example Apparent magnitudeBrightness. relative to. value 0Example Apparent. valueBrightness. relative to. value 0Example

−27	6.31 × 10	Sun	−7	631	supernova SN 1006	13	6.31 × 10	quasar 3C 273. limit 4.5-6 in (11-15 cm) telescopes
−26	2.51 × 10	−6	251	ISS (max.)	14	2.51 × 10	Pluto (max). limit 8-10 in (20-25 cm) telescopes
−25	10	−5	100	Venus (max.).	15	10
−24	3.98 × 10	−4	39.8	The dimmest objects visible to the naked eye during the day when the sun is high	16	3.98 × 10	Charon (max.)
−23	1.58 × 10	−3	15.8	Jupiter (max.), Mars (max.)	17	1.58 × 10
-22	6.31 × 10	−2	6.31	Mercury (max.)	18	6.31 × 10
−21	2.51 × 10	−1	2.51	Sirius	19	2.51 × 10
−20	10	0	1	Vega, Saturn (max.)	20	10
−19	3.98 × 10	1	0.398	Antares	21	3.98 × 10	Callirro (a satellite of Jupiter).
−18	1.58 × 10	2	0.158	Polaris	22	1.58 × 10
−17	6.31 × 10	3	0.0631	Cor Caroli.	23	6.31 × 10
– 16	2.51 × 10	4	0.0251	Acubens	24	2.51 × 10
−15	10	5	0.01	Vesta (max.), Uranus (max.)	25	10	Fenrir (satellite of Saturn).
−14	3.98 × 10	6	3.98 × 10	typical naked eye limit	26	3.98 × 10
−13	1.58 × 10	full moon	7	1.58 × 10	Ceres (max).	27	1.58 × 10	visible light limit of 8-meter telescopes
−12	6.31 × 10	8	6.31 × 10	Neptune (max.)	28	6.31 × 10
−11	2.51 × 10	9	2.51 × 10	29	2.51 × 10
−10	10	10	10	typical limit of 7 × 50 binoculars	30	10
−9	3.98 × 10	iridium flash (max.)	11	3.98 × 10	Proxima Centauri	31	3.98 × 10
−8	1.58 × 10	12	1.58 × 10	32	1.58 × 10	HST visible light limit

Different Measurements

Under Pogson’s system, Vega has been designated as the primary reference star, with an apparent magnitude of zero, regardless of the method of measurement or wavelength filter used. This is the reason why stars brighter than Vega, such as Sirius (with a stellar magnitude of -1.46 or -1.5), have negative magnitudes. However, in the late 20th century, it was discovered that Vega’s brightness varies, which makes it unsuitable as an absolute reference. As a result, the reference system was updated to be independent of the stability of any specific star. This is why the modern value of Vega’s stellar magnitude is close to zero, but not exactly zero. In fact, it is approximately 0.03 in the V (visual) range. The current absolute reference systems include the AB magnitude system, where the reference source is defined by a constant flux density per unit frequency, and the STMAG system, where the reference source is defined by a constant flux density per unit wavelength.

Challenges

The human visual perception can be easily deceived, and the Hipparchus scale encountered various challenges. One such challenge is the discrepancy between the sensitivity of the human eye to yellow and red light compared to blue light, as well as the varying sensitivity of photographic film to blue and yellow/red light. This discrepancy results in different measurements of visual magnitude and photographic magnitude. Additionally, the apparent magnitude may also be influenced by factors like atmospheric dust or light cloud cover, which can absorb certain amounts of light.

Related articles

• Astronomy Portal
• Stellar magnitude AB
• Color-color chart
• List of brightest stars
• Photometric standard
• UBV-photometric system

Additional information

References

External sources

Actually, the magnitudes of stars can vary. This is because there are no identical celestial bodies in our vast Universe. Of course, there are similarities and common parameters that we use to categorize objects. However, there will always be at least a slight distinction between them.

In the field of astronomy, stellar magnitude refers to a dimensionless numerical measure of an object’s brightness. It represents the amount of energy emitted by the star in the form of photons per unit area per second.

What is the definition of stellar magnitudes?

Astronomy distinguishes between two types of stellar magnitudes: apparent and absolute.

Apparent magnitude

The apparent magnitude measures the visible brightness of stars and is used to describe their visual magnitudes across different ranges such as ultraviolet and infrared.

This measure is actually dependent on the luminosity and distance of the star.
The smaller the apparent luminosity of a star, the brighter it actually is.

Stellar Magnitude Determination

The absolute magnitude is employed here to provide the most accurate characterization of the celestial object, which is equivalent to the value at a distance of 10 parsecs away from it. When comparing the luminosity of stars, the absolute magnitude is utilized, as it is independent of their distance from us.

Furthermore, in order to compute the luminosity, it is necessary to ascertain the absolute value of the star’s brightness.

How stellar magnitude is calculated

In the 2nd century BC, Hipparchus, an astronomer from Ancient Greece, was the first to divide stars by their magnitude. He classified the brightest stars as first magnitude and the dimmest stars as sixth magnitude.
Simply put, a first magnitude star is the brightest in the sky.

Hipparchus introduced this classification, and over time, other scientists have contributed to the knowledge about celestial bodies.

In 1856, Norman Pogson proposed a different calculation for the magnitude scale, which became widely accepted.

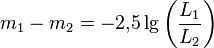
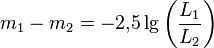
Pogson’s formula is used to calculate the difference between the magnitudes of celestial bodies. In the formula, m represents the stellar magnitude of the body, and L represents its luminosity.
It is important to note that Pogson’s formula can only be used to calculate the difference between magnitudes, not the actual magnitudes themselves. This is because the calculation requires a zero point, which corresponds to the luminosity of a reference star.

In the past, the zero point was defined as the luminosity of Vega. However, over time, it has been redefined. Nevertheless, when visually observing celestial bodies, Vega is still considered the zero-measure.

It has been discovered that objects with the highest brightness possess a negative value for their stellar magnitude.

By the way, in contemporary astronomy, stellar magnitudes are utilized not only for stars but also for planets and other celestial objects. However, when characterizing them, both the apparent and absolute values are taken into consideration.

Therefore, the luminosity of stars and their stellar magnitude serve as significant indicators of the object. Naturally, they are influenced by other chemical and physical properties of the celestial body.

The brilliance of stars shines brightly in the night sky. Nevertheless, modern instruments and technology enable astronomers to observe high magnitude stars. In other words, it has become feasible to even detect the faintest of stars.

When we gaze up at the night sky, we can immediately observe that stars differ greatly in terms of their brightness. And it is important to quantitatively describe this disparity. To make things simpler, let’s begin with everyday examples.

Imagine that we want to rank all the businesspeople on Earth based on their “financial coolness.” The range of “coolness” spans from tens of billions of dollars for billionaires to just one dollar for young boys playing for money.

Is it possible to create a scale that encompasses this vast range?

Surprisingly, it is indeed possible, and it’s not even very complicated.

Let’s designate a businessperson with ten billion dollars (N=10 10 $) as a businessperson of the first magnitude (m=1).

A businessperson with one billion dollars (N=10 9 $)

A person of moderate importance in the business world (m=2).

You obtain this type of “level of sophistication” that encompasses the entire vast spectrum:

Condition
Coolness

N=10 10 $	m=1
N=10 9 $	m=2
N=10 8 $	m=3
N=10 7 $	m=4
N=10 6 $	m=5
N=10 5 $	m=6
N=10 4 $	m=7
N=10 3 $	m=8
N=10 2 $	m=9
N=10 1 $	m=10
N=10 0 $	m=11

Suppose we have a businessman of fifth magnitude who is hundred times wealthier than a businessman of seventh magnitude. We can represent this using a simple formula:

(1).

or for those familiar with logarithms,

(1′).

Here’s another example: let’s consider classifying Earth’s settlements based on their population, which can range from single units (like a farm) to tens of millions (like megacities). How can we group such a wide range into a small number of categories? In other words, how can we create a population scale?

We can label settlements with a population of ten million (N=10 7) as settlements of the first magnitude (m=1).

Settlements with a population of one million (N=10 6) would be classified as settlements of the second magnitude (m=2).

Similarly, settlements with a population of hundred thousand (N=10 5) would be considered as settlements of the third magnitude, and so on.

The data below represents the “population scale”:

N=10 7 $	m=1
N=10 6 $	m=2
N=10 5 $	m=3
N=10 4 $	m=4
N=10 3 $	m=5
N=10 2 $	m=6
N=10 1 $	m=7
N=10 0 $	m=8

It appears that if the values m differ from one another by a single unit, the population differs by a factor of 10. If the values differ by 2 units, the population differs by a factor of 100. Once again, this relationship can be expressed using the formula (check)

(1).

For practice, you can now create a scale of mammal weights, ranging from a shrew weighing 5 grams to a blue whale weighing 190 tons. Alternatively, you can create a scale of counting device speeds, ranging from one operation per second (using the “ten fingers” method) to ten trillion operations per second (the fastest computer at the time of writing this text). Now, let’s move on to the scale of stellar magnitudes.

2. The scale of star brightness

Primitive civilizations observed that stars vary in their brightness. In the second century B.C., the Greek astronomer Hipparchus introduced a system to classify stars based on their brightness. He divided all stars into six magnitudes. The most luminous stars in the sky, such as Sirius, Arcturus, Vega, Capella, and a few others, were classified as “stars of the first magnitude”, while stars that were barely visible to the naked eye were categorized as “stars of the sixth magnitude.”

In the 19th century, two millennia after Hipparchus, scientists learned to measure the brightness of stars (the amount of radiation that falls on a specific area). They discovered that stars of the first magnitude are X times brighter than stars of the second magnitude, which are X times brighter than stars of the third magnitude, and so on. This pattern of brightness in stars follows a similar pattern to the success of businessmen. The only difference is that in the business world, each step represents a factor of ten, while in the scale of star brightness, the value of X still needs to be calculated. However, it is known that stars of the first magnitude are exactly 100 times brighter than stars of the sixth magnitude.

Thus, we can arrange the brilliance of stars in terms of steps:

However, conversely, based on equation (2), E1/E6 = 100, it follows that Х 5 = 100, and therefore

(4).

Now, all the relationships in table (3) can be expressed in the form of a single “slope formula” that connects the stellar magnitudes n and k with the intensity of the star’s luminosity

(5).

(5′).

It is simple to verify that table (3) is indeed derived from this formula. And for those who are already well-versed in logarithms, we can express this equality as follows:

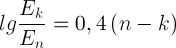
(6).

(6′).

I would like to transform the star magnitude from being just a “grade in points” (since different excellent students and different third graders may have different levels of mastery) into a complete physical quantity. In order to achieve this, we need to establish the physical value of a star’s luminosity (which refers to the intensity of its radiation or illuminance). To accomplish this, we have taken the following steps: we have introduced a “zero magnitude star” called Vega from the constellation Lyra, measured the luminosity it emits (i.e., the intensity of its radiation), and designated it as Е0.

Now, using formulas (5) or (5′), we can determine the radiation intensity (luminosity) of any celestial body.

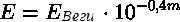
(8).

Alternatively, one can determine the luminosity produced by a particular source (e.g., a spotlight) and then compute the “stellar magnitude” of the object using equations (6) and (6′):

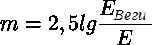
(8′).

3. What factors determine the magnitude of a star?

Obviously, the magnitude of a star depends on two factors: the total power that the star radiates and the distance between the star and the observer. This relationship can be easily established and expressed using a simple formula. By knowing the radiating power and the apparent magnitude, one can determine the distance. Conversely, by knowing the stellar magnitude and distance, one can determine the luminosity.

Let’s consider a star that emits light power L (referred to as luminosity), and an observer located at a distance r from the star. If we imagine surrounding the star with a sphere of radius r, the energy per unit surface area of the sphere can be calculated.

(9),

This is the precise luminosity, expressed in W/m2. Therefore, evidently,

(9′),

By substituting (8) here, we can represent the luminosity of the star in terms of its stellar magnitude and the distance to it

(10),

4. Absolute stellar magnitude.

Thus, it appears that the apparent stellar magnitude relies on both the luminosity of the star and the distance to it. If we desire to compare stars solely based on their luminosity, we must examine all stars from an equal distance. In reality, we are unable to alter the distance to stars, but we can accomplish this through a “mental experiment”.

Let’s assume a star with a luminosity of L is located at a distance of r1, then its apparent magnitude m is also known. Let’s envision moving it to a standard distance

At a distance of approximately 10 17 meters (which is equivalent to about 33 light years), the stellar magnitude visible is denoted as m. The absolute stellar magnitude is represented by M. A relationship between the absolute magnitude M and the apparent magnitude m can be established using formulas (5) and (9):

(11),

where E2 represents the luminosity that the star would produce at a distance r2,

E1 represents the luminosity that it actually gives off while being at a distance r1.

Since the star remains the same, the luminosity L remains unchanged. Therefore, by substituting formula (9) into (10), we obtain

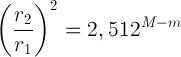
(12),

or, bearing in mind that according to equation (4)

,

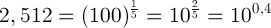
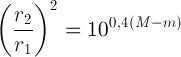
(12′),

Taking the logarithm of both sides, the equation becomes

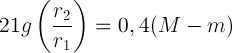
In this proportion, all values are known except for the unknown value M, which we can determine:

(13),

For instance, for the Sun, with m = -26.8, r1 = 1.5×10 11 m, and r2 = 10 parsecs ≈ 3.2×10 17 m, we can find M = 4.7. This means that the Sun, from a distance of 10 parsecs, will appear as a faint star with a magnitude of approximately fifth.

Below is a table displaying the brightest stars and their corresponding magnitudes.

Object
Constellation
m

Sirius	Canis Major	−1.47
Canopus	Carina	−0.72
Alpha Centauri	Centaurus	−0.27
Arcturus	Bootes	−0.04
Vega	Lyra	+0.03
Capella	Auriga	+0.08
Rigel	Orion	+0.12
Procyon	Canis Minor	+0.38
Achernar	Eridanus	+0.46
Betelgeuse	Orion	+0.50
Altair	Aquila	+0.75
Aldebaran	Taurus	+0.85
Antares	Scorpius	+1.09
Pollux	Gemini	+1.15
Fomalhaut	Piscis Austrinus	+1.16
Deneb	Cygnus	+1.25
Regulus	Leo	+1.35

Stellar magnitude is a dimensionless quantity that assigns a numerical value to the brightness of a star or any other celestial body relative to its visible area. Put simply, this magnitude represents the amount of electromagnetic waves emitted by the body that are detected by an observer. As a result, this value is influenced by both the properties of the observed object and the distance between the object and the observer. It’s important to note that this term only applies to the visible, infrared, and ultraviolet spectra of electromagnetic radiation.

The term “brilliance” is also used to describe point light sources, while “brightness” refers to extended light sources.

The Origins of the Star Catalog

Hipparchus of Nicaea, a renowned ancient Greek scientist who resided in Turkey during the 2nd century BC, is widely regarded as one of the most influential astronomers of his time. He meticulously compiled a comprehensive catalog of stars, which was the first of its kind in Europe, detailing the precise locations of over a thousand celestial luminaries. Additionally, Hipparchus introduced the concept of stellar magnitude. By observing these stars with the naked eye, the astronomer sought to classify them based on their brightness, dividing them into six magnitudes. The first magnitude denoted the brightest objects, while the sixth magnitude represented the faintest ones.

During the 19th century, the British astronomer Norman Pogson made advancements to the scale used to measure the brightness of stars. Pogson expanded the range of values and introduced a logarithmic relationship. This means that as the magnitude of a star increases by one, the brightness of the object decreases by a factor of 2.512. Therefore, a star with a magnitude of 1m is one hundred times brighter than a star with a magnitude of 6m.

Vega serves as the standard for measuring stellar magnitude.

The standard for celestial objects with zero stellar magnitude was initially set to be the brightness of Vega, the brightest star in the Lyra constellation. Later on, a more precise definition of an object with zero stellar magnitude was established – its illuminance should be equal to 2.54-10-6 lux, and the light flux in the visible range should be 106 quanta/(cm²-s).

The characteristic mentioned earlier, initially defined by Hipparchus of Nicaea, later became recognized as “visible” or “visual”. This means that it can be observed both by the human eye within the visible spectrum and by various instruments such as telescopes, which can detect ultraviolet and infrared wavelengths. The stellar magnitude of the Big Dipper constellation is 2m. However, it is important to note that Vega, despite having a stellar magnitude of zero (0m), is not the brightest star in the sky (it ranks fifth in terms of luminosity, and third for observers from the CIS). This suggests that brighter stars may have a negative stellar magnitude, such as Sirius (-1.5m). Furthermore, it is now understood that celestial luminaries can include not only stars, but also objects that reflect starlight, such as planets, comets, and asteroids. The stellar magnitude of a full Moon is -12.7m.

Absolute brightness and luminosity of stars

In order to effectively compare the true brightness of celestial bodies, scientists have devised a measure known as absolute stellar magnitude. This metric allows us to calculate the apparent stellar magnitude of an object if it were positioned 10 parsecs (32.62 light years) away from Earth. By using this standardized distance, we can eliminate the impact of varying distances to the observer when comparing different stars.

The absolute stellar magnitude is also utilized for space objects within our Solar System, but with a different reference point. Specifically, the distance from the body to the observer is measured in astronomical units, with the observer theoretically situated at the center of the Sun.

Resources about the subject

The magnitude system, which is used to measure the brightness of stars, was first introduced by the ancient Greek astronomer Hipparchus. He divided the stars into six different magnitudes, with the brightest stars being assigned a magnitude of one and the faintest stars a magnitude of six. This system is still used today, although it has been expanded to include negative magnitudes for exceptionally bright stars.

However, in modern astronomy, another quantity called “luminosity” is often used to describe the brightness of a star. Luminosity refers to the total amount of energy that a star emits over a certain period of time. It is a more useful measure than magnitude because it takes into account the star’s distance from Earth. The absolute stellar magnitude is a value that can be used to calculate the luminosity of a star.

As previously mentioned, the brightness of stars can be measured for various types of electromagnetic radiation, resulting in different values for each range of the spectrum. In order to capture images of celestial objects, astronomers often utilize photographic plates, which are particularly sensitive to the high-frequency portion of visible light. As a result, stars appear blue in these images. This particular measure of stellar brightness is known as “photographic magnitude” (mPv). However, to obtain a value that is more representative of how stars appear to the human eye (referred to as “photovisual magnitude,” mP), the photographic plate is coated with a specialized orthochromatic emulsion and a yellow light filter is employed.

A photograph of the Sun taken using a dark light filter

Scientists have developed a photometric system that allows them to determine various important characteristics of celestial bodies, such as surface temperature, albedo (excluding stars), and the amount of interstellar light absorption. This system involves capturing images of the celestial object in different spectra of electromagnetic radiation and then comparing the results. The most commonly used filters for these photographs are ultraviolet, blue (for measuring stellar magnitude), and yellow (similar to the photovisual range).

A photograph containing the captured energies of various electromagnetic waves determines the bolometric stellar magnitude (mb), which is a measure of the total energy emitted by a star. Using this information, astronomers can calculate the luminosity of a celestial body by taking into account the distance and the amount of interstellar absorption.

Stellar Magnitudes of Selected Objects

• The Sun = -26.7m
• The Full Moon = -12.7m
• Iridium Flash = -9.5m. Iridium is a system of 66 satellites orbiting the Earth and is used for transmitting voice and other data. Periodically, the surface of each of the three main satellites reflects sunlight towards Earth, creating a brief but intense flash of light in the sky that can last up to 10 seconds.

• The most intense explosion of a supernova, which occurred in 1054, is thought to have led to the formation of the Crab Nebula and had a magnitude of -6.0. According to ancient Chinese and Arab astronomers, the supernova was visible for a period of 23 days, even in daylight, without the aid of telescopes.
• Venus at its brightest has a magnitude of -4.4.
• From the perspective of an observer on the Sun, the Earth has a magnitude of -3.84.
• Mars at its maximum brightness has a magnitude of -3.0.
• Jupiter at its brightest has a magnitude of -2.8.
• The International Space Station at its maximum brightness has a magnitude of -2.

The International Space Station’s trajectory intersects with the captivating Big Dipper constellation.

• α Centauri has a magnitude of -0.27
• Vega shines at a magnitude of +0.03
• The Andromeda Galaxy has an impressive magnitude of +3.4
• Faint stars that can still be perceived by the human eye have a magnitude range of +6 to +7
• Proxima Centauri has a magnitude of +11.1
• The brightest quasar has a magnitude of +12.6
• Ground-based telescopes, such as 8-meter telescopes, can detect objects with a magnitude of +27
• The Hubble Space Telescope can detect objects with a magnitude of +30

On a clear night, an individual can observe approximately two to three thousand stars in the night sky without the aid of any optical devices. However, despite the abundance of stars, they all appear quite similar, making it difficult to differentiate between them. Fortunately, this video lesson offers valuable insights into the world of astronomy. By watching this lesson, you will gain knowledge about the various constellations and their unique names. Additionally, you will discover the meaning of stellar magnitude and understand the principles of the Hipparchus scale of stellar magnitudes. Lastly, you will become familiar with the Bayer star classification system, which is an essential tool in the field of astronomy.

Currently, it is not possible to view or share the video tutorial with students

In order to access this and other video tutorials in the package, you will need to add it to your personal account.

Unlock amazing functionalities

Outline of a Lesson on Stars and Constellations

During a cloudless night, an array of stars brightly illuminate the sky, creating a breathtaking sight. It can be overwhelming to comprehend this magnificent celestial display. The words of the renowned Russian scientist and poet, Mikhail Vasilyevich Lomonosov, come to mind:

The vast expanse is adorned with countless stars,

An infinite number of stars, an unfathomable abyss.

Indeed, on a clear night, the naked eye can perceive approximately 2-3 thousand stars. However, they all appear remarkably similar, making it challenging to differentiate between them.

Ancient Egyptian astronomers were determined to solve this quandary. To enhance their understanding of the expansive starry sky, they grouped certain stars together and linked them with imaginary lines, thus creating constellations.

The ancient Greeks were particularly successful in their efforts to create constellations. They achieved this by grouping stars together and giving them names inspired by their legendary heroes, mythical characters, and even animals.

This particular task proved to be highly practical due to the fact that the invention of the compass had not yet taken place, making the stars an essential point of reference during nighttime. In his monumental work “Almagest” (a comprehensive mathematical construction of astronomy consisting of 13 books), the renowned Greek astronomer Claudius Ptolemy documents a total of 48 constellations, including well-known ones such as the Big Dipper, Little Dipper, Orion, Hercules, Scorpius, and many others.

Many constellations have peculiar names because it can be challenging to spot or even imagine certain animate beings when looking at them. Take the Big Dipper, for instance, which some individuals struggle to identify within the starry bucket. This constellation is one of the largest and most easily recognizable, boasting a total of 210 stars visible to the naked eye.

The names of many prominent constellations derive from the traditions of various nations. For instance, the ancient Slavs depicted the Big Dipper as an Elk or a Deer.

Around the 3rd century BC, ancient Greek astronomers unified the names of all known constellations into a single system closely tied to their mythology. Eventually, European science adopted these names as well.

Regarding the Southern Hemisphere, its constellations were named during the era of significant geographical discoveries when Europeans embarked on exploring the New World.

However, astronomy faced a complex situation over time. Prior to the 19th century, scientists worldwide understood constellations not as sky regions but as specific groups of stars, often overlapping with each other. It was discovered that some stars belonged to multiple constellations, while certain star-scarce areas did not belong to any constellation at all. Therefore, in the early 19th century, borders were drawn between constellations on the celestial sphere to eliminate the “voids” between them. Yet, this did not resolve the issue completely, as there was still no precise definition of constellations, and different astronomers defined them in their own unique ways.

In the year 1922, in the city of Rome, the General Assembly of the International Astronomical Union officially sanctioned a total of 88 constellations. Furthermore, in the year 1928, precise and unmistakable boundaries between these constellations were established. Simultaneously, astronomers made a solemn agreement that they would never alter the boundaries or names of these constellations in the future.

In the present day, constellations are defined as specific regions of the celestial sphere, which are demarcated by precisely determined boundaries and exhibit a distinctive arrangement of observable stars.

As previously mentioned, when the sky is clear at night, we are able to observe approximately three thousand stars with the naked eye. Each of these stars possesses its own unique level of brightness, with some stars being easily visible while others are more difficult to discern. Thus, in the 2nd century BC, the renowned ancient astronomer Hipparchus of Nicaea categorized all stars into six different stellar magnitudes. The first stellar magnitude was designated for the brightest stars, while the sixth magnitude was assigned to the least noticeable ones. The remaining stars were evenly distributed among the intermediate magnitudes.

The system of stellar magnitudes continues to be widely utilized in modern times. Stellar magnitudes are indicated by the symbol m (derived from the Latin term ‘magnitude’), which is positioned above the numerical value.

In addition, ancient Greek and Arabic astronomers assigned unique names to approximately 300 of the most brilliant or intriguing stars, such as Vega, Sirius, Rigel, Aldebaran, and others.

In 1603, the German astronomer Johann Bayer introduced his star naming system, which is still in use today. This system involves two components: the name of the constellation to which the star belongs and a letter from the Greek alphabet. Generally, the letter designation is assigned in descending order of the star’s brightness within the constellation.

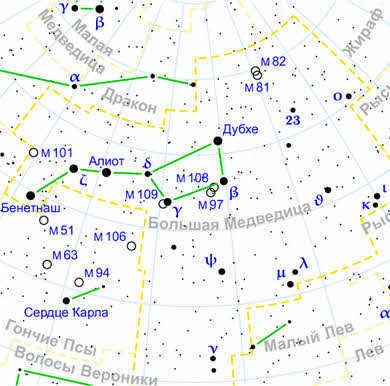
For instance, the most brilliant star in our celestial sphere, Sirius, is marked on charts as α of Canis Major, and Polaris is α of Ursa Minor.

Significantly missing from this inventory is the group of stars known as Ursa Major, whose seven luminous stars create the renowned Big Dipper. The assignment of names to these stars was based solely on their arrangement from right to left.

Therefore, the outermost star of the Big Dipper, Dubhe, is known as the alpha of the constellation, even though it is not as bright as Aliot, the epsilon of the Big Dipper. Additionally, the third brightest star in this constellation, Benetnash, is commonly referred to as the eta.

As science advanced and telescopes were invented, the number of stars being studied increased. Using Greek letters for designation was no longer sufficient. As a result, it was suggested to use letters from the Latin alphabet. Eventually, even the Latin letters ran out, and stars began to be designated by numbers (for example, the star 44 Volopassus).

Over time, it became apparent that Hipparchus’ estimates of stellar magnitudes for more than a hundred stars were quite imprecise. Specifically, it was discovered that the human eye responds to the energy of light that has passed through the pupil. However, this response is independent of the size of the pupil. Instead, it is related to the luminosity, which refers to the flux of radiation that comes from the light source to the observer per unit time per unit area perpendicular to the beam of vision. Therefore, stellar magnitude can be seen as a measurement of the illuminance generated by the observed source. In modern astronomy, the term used for this concept is luminosity.

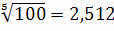
Following the development of photometers in the 19th century, a new era in the exploration of star brightness and their systems began. These instruments allowed for the measurement of luminosity, revealing that a difference of five stellar magnitudes on the Hipparchus scale corresponds to a luminosity ratio of almost 1:100. This discovery prompted the creation of a new scale, where this ratio would be precisely 1:100. Consequently, each stellar magnitude difference represents a ratio of star illuminance equal to .

To simplify, a first magnitude star has a luminosity 2.512 times greater than that of a second magnitude star. Similarly, a second magnitude star has a luminosity that exceeds a third magnitude star by the same factor, and so on.

The scale of stellar magnitudes was formalized by the English astronomer Norman Robert Pogson, who proposed a pattern that was later widely adopted.

The Pogson relation provides a method for calculating the magnitudes of stars, including those that are brighter than the first stellar magnitude. As a result, there are several stars in the sky that have been classified as having a magnitude of zero. For instance, Sirius, the brightest star in the entire sky, has a negative magnitude of -1.5 m.

Additionally, we can use this relation to determine the difference in illumination between the full moon and the first quarter phase of the Moon.