- The individual responsible for discovering the three laws of planetary motion is not associated with scientific work and did not complete a graduate qualification work!
- This particular type of work is a finalized product of processing, organizing, and formatting the gathered information, which is meant to be used as a resource for independently preparing academic work.
If you are facing difficulties in grasping the subject, feel free to contact me on WhatsApp. We can discuss your topic, come to a mutual understanding, and agree on the terms. I am here to assist you!

If you are interested in acquiring the skills to effectively execute and compose essays on various topics, I have provided comprehensive information on the webpage titled “Understanding Essays and Mastering the Art of Writing Them”.

Introduction
When man studies natural phenomena, he gains an understanding of their essence and uncovers the laws that govern them. For instance, if a body is elevated above the Earth and left to its own devices, it will eventually start to descend. This change in motion is a result of the force of gravity acting upon it. This phenomenon is observed universally on our planet – the Earth exerts gravitational attraction on all objects, including ourselves. But is gravity solely an Earth-bound force?
In the solar system, nearly everything revolves around the Sun. While some planets have their own satellites, these satellites travel in sync with their respective planets as they orbit the Sun. The mass of the Sun is a staggering 750 times greater than the combined mass of the entire solar system. This immense mass causes the Sun to exert a gravitational pull that keeps the planets and other celestial bodies in their orbits. Mass, on a cosmic scale, is the primary characteristic that determines how bodies behave, as all celestial bodies follow the law of universal gravitation.
Isaac Newton, a renowned English scientist, made a groundbreaking discovery in the field of planetary motion based on the laws established by I. Kepler. Newton’s law of universal gravitation, which he developed while still relatively unknown, allowed for precise calculations of the movement of celestial bodies such as the Moon, planets, and comets. Additionally, this law provided an explanation for the phenomenon of ocean tides.
These laws have proven invaluable not only for expanding our understanding of the natural world, such as determining the masses of celestial bodies, but also for solving practical problems in fields like astronautics and astrodynamics.
Kepler’s laws: The fundamental principles governing the motion of planets
To fully comprehend the vibrant nature of the discovery of the Universal Law, let’s rewind to its prehistory. Legend has it that while strolling through an apple orchard on his family’s estate, Newton witnessed the moon gracing the daytime sky, and right before his eyes, an apple detached from a branch and descended to the ground. As Newton was engrossed in his research on the laws of motion during this time, he was well aware that the apple’s descent was due to the Earth’s gravitational field. Moreover, he understood that the Moon was not merely suspended in the sky, but rather it orbited the Earth, indicating the existence of a force that kept it from straying out of orbit and hurtling straight into the vast expanse of space. This revelation led him to surmise that this force could be the same one responsible for the apple’s fall to the Earth and the Moon’s continued presence in Earth’s orbit – the force of gravity, which permeates between all celestial bodies.
The concept of a universal gravitational force had been proposed multiple times in the past: Epicurus, Gassendi, Kepler, Borelli, Descartes, Roberval, Huygens, and others had contemplated it. Descartes believed that it stemmed from vortices in the ether. The scientific record reveals that nearly all theories regarding the movement of celestial bodies prior to Newton were essentially founded on the notion that these bodies, being flawless, travel in circular paths due to their perfection, given that the circle is a faultless geometric shape.
Therefore, to modernize the concept, it was widely believed that there existed two distinct forms of gravitational force, and this notion was deeply ingrained in the collective consciousness of the era. The general consensus was that terrestrial gravity exerted its influence on the imperfect Earth, while celestial gravity governed the flawless heavens. Through the meticulous observation of planetary motion and the analysis of the solar system’s structure, the revolutionary theory of gravity gradually took shape – culminating in the groundbreaking discovery of the law of universal gravitation.
One of the earliest endeavors to construct a comprehensive model of the cosmos was undertaken by Ptolemy in approximately 140 AD. Ptolemy’s geocentric system placed the Earth at the epicenter of the Universe, with the planets and stars revolving around it in intricate circular patterns, akin to an elaborate dance. Remarkably, Ptolemy’s geocentric model persisted for over 14 centuries, only to be supplanted by Copernicus’ heliocentric system in the midst of the 16th century.
In the early 17th century, I. Kepler, a German astronomer, formulated three empirical laws of planetary motion based on the Copernican system and using observations made by Danish astronomer T. Brahe.
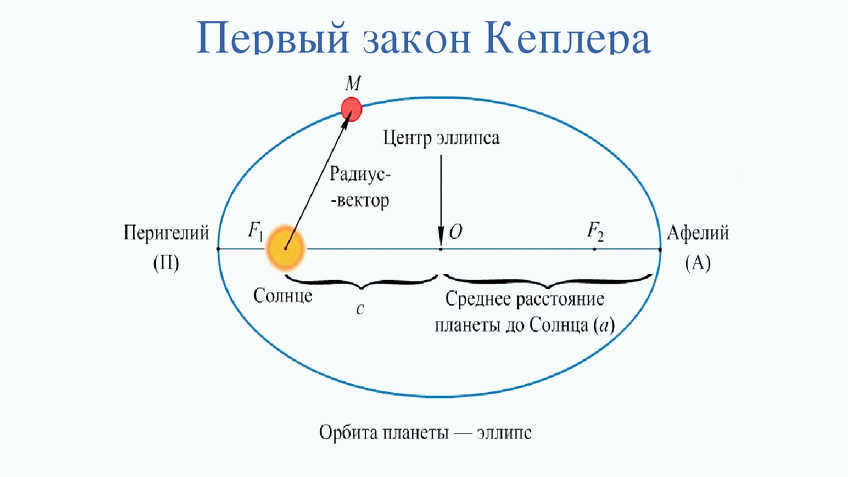
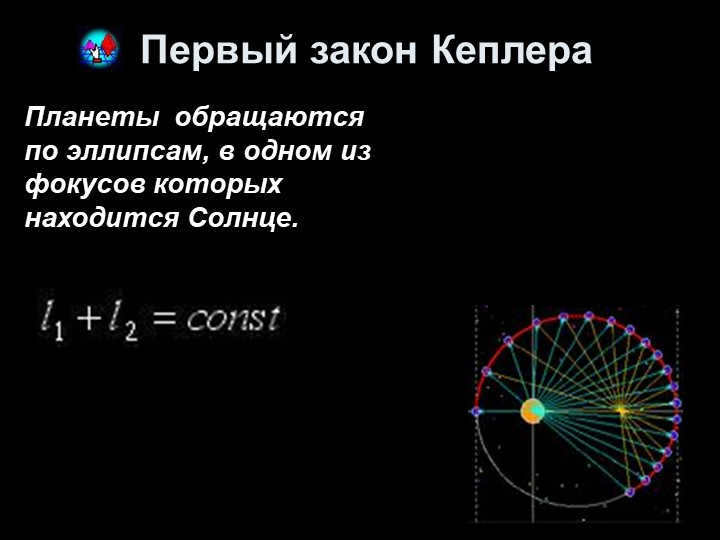
Kepler’s first law (1609) states that all planets move in elliptical orbits, with the Sun located at one of the foci of the ellipse.
The shape of the ellipse is determined by the planet’s speed and distance from the center. If the velocity of a celestial body changes, its elliptical orbit can transform into a hyperbolic orbit, allowing it to potentially escape the boundaries of the solar system.
Kepler’s second law demonstrates that the areas described by the radius-vector of a celestial body for equal time intervals are equal. In this scenario, the velocity of the body changes based on its distance from the Earth (which is especially noticeable when the body follows a highly elongated elliptical orbit). The closer the body is to the planet, the greater its velocity.
Kepler’s Third Law (1619) states that “the squares of the orbital periods of the planets are proportional to the cubes of the major semi-axes of their orbits”; or, in other words, Kepler’s Third Law holds true for all planets in the solar system with an accuracy of better than 1%.
Kepler’s laws, which have become the foundation of theoretical astronomy, were explained in Isaac Newton’s mechanics, particularly in the law of universal gravitation.
Although Kepler’s laws marked a significant advancement in comprehending the planetary motion, they remained merely empirical principles derived from astronomical observations. Kepler was unable to identify the underlying cause behind these universal patterns exhibited by all planets. Therefore, Kepler’s laws required theoretical validation.
It was only Newton who arrived at a crucial private conclusion: there must exist a correlation between the centripetal acceleration of the Moon and the acceleration of free fall on Earth. This link needed to be established and numerically verified.
This is where Newton’s insights diverged from the speculations of other scientists. Prior to Newton, no one had managed to clearly and mathematically establish a connection between the law of gravitation (the force being inversely proportional to the square of the distance) and the laws governing planetary motion (Kepler’s laws).
They never crossed paths at the time. However, it is worth mentioning that Newton was born just thirteen years after Kepler’s death. Interestingly, both of them were supporters of Copernicus’ heliocentric system.
Kepler spent many years studying the motion of Mars and during this time he experimentally discovered the three laws of planetary motion, more than fifty years before Newton discovered the law of universal gravitation. It still puzzles me why the planets move in this particular way and not the other way around. It was truly a brilliant insight.
On the other hand, Newton precisely verified his law of universal gravitation using Kepler’s laws. It turns out that all three of Kepler’s laws are consequences of the law of universal gravitation, a discovery made by Newton. These calculations by Newton are now referred to as Newton’s law of universal gravitation, which we will delve into in the following chapter.
The Law of Universal Gravitation
The Discovery by Isaac Newton
Isaac Newton made the groundbreaking discovery of the law of universal gravitation in 1682. According to his hypothesis, gravity, the force of attraction, acts between all bodies in the universe along a line that connects their centers of mass. In the case of a homogeneous ball, the center of mass coincides with the center of the ball.
In the years that followed, Newton embarked on a quest to provide a physical explanation for the laws of planetary motion, which were initially discovered by Johannes Kepler in the early 17th century. Additionally, Newton sought to establish a quantitative expression for gravitational forces. By studying the movements of planets, Newton aimed to determine the forces at play, a problem known as the inverse problem of mechanics.
If the primary objective of mechanics is to ascertain the coordinates and velocity of a known mass body at any given moment in time based on known forces and initial conditions (the direct problem of mechanics), then in tackling the inverse problem, it becomes necessary to determine the forces acting on the body if its motion is known.
Solving this quandary led Newton to the discovery of the law of universal gravitation: “All objects are attracted to each other with a force that is directly proportional to their masses and inversely proportional to the square of the distance between them.” Like all laws in physics, it is expressed in the form of a mathematical equation.
The proportionality coefficient G remains constant for all bodies in nature and is known as the gravitational constant.
G = 6.67 x 10^-11 N – m^2 / kg^2 (SI)
There are a number of significant observations that can be made regarding this legislation.
Initially, it is clear that the legislation applies to all physical objects in the universe, without exception. This means that both you and the book, for example, experience forces of mutual gravitational attraction that are equal in magnitude but opposite in direction. While these forces are incredibly minuscule and cannot be detected by even the most precise modern instruments, they still exist and can be calculated.
Similarly, you also experience mutual gravitational attraction with a distant quasar that is located tens of billions of light years away. Once again, the forces of this attraction are too weak to be recorded or measured by instruments.
Another aspect to consider is that the Earth’s gravitational force acts uniformly on all objects regardless of their location. At this very moment, we are experiencing the gravitational pull, as indicated by the formula mentioned above, which determines our weight. If we were to release an object under the same force, it would descend to the ground with the same acceleration.
The phenomenon of gravity in the natural world is responsible for explaining a multitude of occurrences: such as the orbit of planets within the solar system, the trajectories of artificial satellites, the flight paths of ballistic missiles, and the movement of objects in close proximity to the Earth’s surface. All of these phenomena can be explained by the principles of the law of universal gravitation and the laws of dynamics.
The law of universal gravitation is responsible for explaining the mechanical structure of our solar system, with Kepler’s laws providing insight into the paths that planets take. Kepler himself viewed his laws as purely descriptive, summarizing his observations in a mathematical format without providing any theoretical basis for the formulas. However, in Newton’s comprehensive system of cosmic order, Kepler’s laws are seen as a direct result of the universal laws of mechanics and the law of universal gravitation. This demonstrates how empirical findings at one level can be transformed into logically sound conclusions as our understanding of the world deepens.
Newton was the first person to propose the concept that gravitational forces not only control the movement of planets within the solar system, but also act between all objects in the universe. One example of this universal gravitational force is gravity, which refers to the attraction of objects towards the Earth’s surface.
Gravity always pulls objects towards the center of the Earth. In the absence of any other forces, objects will fall freely towards the Earth with the acceleration of free fall.
The average value of free fall acceleration at different locations on the Earth’s surface is 9.81 m/s2. By knowing the free fall acceleration and the radius of the Earth (rg = 6.38 x 106 m), it is possible to calculate the mass of the Earth.
Imagine a scenario where we have filled the cannon with an enormous amount of gunpowder, giving the cannon enough velocity to orbit the entire planet. Assuming that air resistance is not a factor, the nucleus, after completing a full orbit around the Earth, will return to its initial position with the exact same velocity it had when it was first launched from the cannon. At this point, it is evident that the nucleus will not come to a stop, but rather, it will continue to orbit the planet.
In simpler terms, what we will have is an artificial satellite that revolves around the Earth, much like a natural satellite such as the Moon.
Thus, gradually, we transitioned from explaining the movement of an object descending solely due to the force of “terrestrial” gravity (as exemplified by Newton’s apple) to explaining the movement of a satellite (such as the Moon) as it travels along its orbit, all while maintaining the same gravitational influence from “terrestrial” to “celestial”. It was this comprehension that enabled Newton to unite the two distinct gravitational forces, which had previously been perceived as separate in their essence.
As the distance from the Earth’s surface increases, the force of gravity and the acceleration of free fall change in an inverse square relationship to the distance r from the center of the Earth. A prime example of a system consisting of two interacting bodies is the Earth-Moon system. The Moon is situated at a distance rL = 3.84 – 106 m from the Earth. This distance is approximately 60 times the radius R ‡ of the Earth. As a result, the gravitational acceleration aL caused by gravity in the Moon’s orbit is given by the following equation:
With this acceleration, which is directed towards the center of the Earth, the Moon revolves in its orbit. Therefore, this acceleration is considered centripetal. It can be determined using the kinematic formula for centripetal acceleration.
The concurrence of the outcomes of calculations carried out in various manners substantiates Newton’s theory regarding the unified essence of the force keeping the Moon in its orbit and the force of gravity.
The Moon’s own gravitational field determines the acceleration of free fall gL on its surface. The Moon has a mass 81 times smaller than that of the Earth, and its radius is approximately 3.7 times less than that of the Earth.
The astronauts who touched down on the Moon experienced such feeble gravity. In such circumstances, an individual can execute tremendous leaps. As an illustration, if a person can jump to a height of 1 meter under normal conditions on Earth, on the Moon, they can jump to a height exceeding 6 meters.
The trajectory of a space object can vary depending on its initial velocity. Let’s take the example of a man-made satellite orbiting the Earth in a circular path. These satellites typically fly at altitudes around 200-300 km above the Earth’s surface, with the distance to the Earth’s center being roughly equal to its radius R ‡ . In this scenario, the centripetal acceleration experienced by the satellite due to gravity is approximately equal to the acceleration of free fall, which we denote as g. We can refer to the velocity of the satellite in Earth’s orbit as x1, which is also known as the first space velocity.
Actually, the time it takes for a satellite to orbit around the Earth’s surface in a circular orbit is slightly longer than expected due to the difference in radius between the actual orbit and the Earth’s radius. The movement of the satellite can be compared to free fall, similar to the trajectory of projectiles or ballistic missiles. The only distinction is that the satellite’s velocity is so high that the curvature of its path matches the Earth’s radius.
For satellites traveling on circular paths at a significant distance from the Earth, the strength of the Earth’s gravity weakens in proportion to the square of the trajectory’s radius, r. As a result, in higher orbits, the velocity of satellites is slower compared to those in Earth’s orbit.
The orbital period of a satellite increases as the radius of the orbit increases. By using a radius of approximately 6.6 times the Earth’s radius, the satellite will complete one orbit in 24 hours. When launched in the equatorial plane, this type of satellite will remain stationary above a specific point on the Earth’s surface. These satellites are commonly used in space-based radio communication systems. An orbit with a radius of 6.6 times the Earth’s radius is referred to as a geostationary orbit.
The second space velocity refers to the minimum velocity required for a spacecraft near the Earth’s surface to overcome the force of gravity and become a satellite of the Sun (or an artificial planet). In this scenario, the spacecraft will follow a parabolic trajectory away from the Earth.
If the velocity of the spacecraft, x1, is 7.9 – 103 m/s and is parallel to the Earth’s surface, then the spacecraft will follow a circular orbit at a low altitude above the Earth. When the initial velocity is greater than x1 but less than x2, which is 11.2 – 103 m/s, the spacecraft’s orbit will be elliptical. At an initial velocity of x2, the spacecraft will follow a parabolic trajectory, and at an even higher initial velocity, it will follow a hyperbolic trajectory.
The velocities near the Earth’s surface are as follows:
- x = x1 – circular trajectory;
- x1 < x < x2 - elliptical trajectory;
- x = 11.1 – 103 m/s – highly elongated ellipse;
- x = x2 – parabolic trajectory;
- x > x2 – hyperbolic trajectory;
- trajectory of the moon
Therefore, it has been determined that Newton’s law of universal gravitation governs all movements within the Solar System.
Considering the relatively small mass of the planets and other celestial bodies within the solar system, it can be roughly inferred that their movements in space around the Sun adhere to Kepler’s laws.
All celestial bodies orbit the Sun in elliptical paths, with the Sun located at one of the foci. The closer a celestial body is to the Sun, the greater its orbital velocity (for example, Pluto, the most distant known planet, moves at a speed 6 times slower than that of Earth).
Summary
In this article, we have discussed the concept of the Law of Universal Gravitation.
Isaac Newton established the law of universal gravitation by synthesizing the findings of previous renowned astronomers. The laws of motion of the planets, which were discovered by the German astronomer I. Kepler through the analysis of astronomical observations made by the Danish astronomer Tycho Brahe, played a crucial role in this process. Kepler expressed these laws in the form of three principles.
One of the key principles states that all planets move in elliptical orbits, with the Sun located at one of the foci.
Another principle asserts that the areas described by the radius-vectors of the planets in the same amount of time are identical.
Furthermore, the ratio of the squares of the planets’ revolution periods around the Sun is equal to the ratio of the cubes of the major semi-axes of their orbits.
Newton proposed the existence of gravitational forces between all objects in nature, which he referred to as gravity forces. These forces, also known as the forces of gravity, are evident in various aspects of the universe, including the cosmos, the solar system, and our planet Earth. In his monumental work, The Mathematical Foundations of Natural Philosophy, Newton formulated the law of universal gravitation and established that:
1. The observed planetary motions imply the presence of a central force.
2. Conversely, a central force of attraction leads to elliptical or hyperbolic orbits.
Consequently, this legislation declares that: there is a force of mutual attraction between any two points made of material, which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them, acting along the line that connects these points.
In contrast to the ideas put forth by his predecessors, Newton’s theory had several notable distinctions. Rather than simply providing a presumed formula for the law of universal gravitation, Newton actually presented a comprehensive mathematical model:
- The law of universal gravitation;
- the law of motion (Newton’s second law);
- a system of mathematical investigation methods (mathematical analysis).
When combined, these three elements provide enough information to fully understand the intricate movements of celestial objects, forming the basis of celestial mechanics. Prior to Einstein, no major adjustments were needed to this model, but it became necessary to make essential advancements to the mathematical tools used.
Subsequently, it was discovered that Kepler’s laws and Newton’s law of universal gravitation have a universal nature, with the law of universal gravitation serving as not only the fundamental principle of celestial mechanics, but also playing a crucial role in the examination of various cosmogonic and cosmological processes.
Technically speaking, Newton’s theory of gravitation is no longer heliocentric. In the case of the two-body problem, the planet doesn’t simply orbit around the sun, but both the planet and the sun revolve around a shared center of gravity. This is because the sun not only attracts the planet, but the planet also exerts a gravitational pull on the sun. Eventually, it became evident that it was necessary to consider the influence of the planets on one another. The discovery of the law of universal gravitation demonstrated the ability of a body to “attract” or be attracted to itself and other bodies.
Over time, it became evident that the law of universal gravitation can accurately explain and predict the movements of celestial bodies, and it came to be regarded as a fundamental principle.
- Gromov S.V. Physics. 9 class / S.V. Gromov. – Moscow: Prosveshchenie, 2004. – 158 pages.
- Kasatkina, I.L. Physics tutor / I.L. Kasatkina. – M .: Phoenix, 2004. – 368 pages.
- Kasyanov, V.A. Physics. Textbook. 10 class / V.A. Kasyanov. – M .: Drofa, 2004. – 416 pages.
- Myakishev G.Ya. Physics: Textbook. for 10 kl. general education. institutions / G.Ya. Myakishev, B.B. Bukhovtsev, N.N.. Sotsky. – M .: Prosveshchenie, 2005. – 399 pages.
Take a look at similar essay topics as they might be useful to you:

The Enigma of the Cosmos
It is worth mentioning that astronomers in the late 16th century were still uncertain about the organization of the solar system and were divided into two factions: some adhered to Ptolemy’s belief that all the planets, the Sun, the Moon, and the stars orbited around the fixed Earth. Others sided with Copernicus and believed that the Sun was the center of the Universe, with the other celestial bodies of the solar system revolving around it. Around 1580, Danish astronomer Tycho Brahe proposed a compromise: all the planets, except for Earth, revolve around the Sun, while Earth remains stationary at the center, causing the Sun and the Moon to orbit around it. This led to the creation of a hybrid geogeliocentric system, merging the geocentric and heliocentric models. However, many questions still remained unanswered, such as the exact rotation of the planets, their trajectory, and speed.
Johannes Kepler took on these inquiries. At 25 years old, he composed a book called The Mystery of the Universe, which examined the six known planets at the time. In this book, he compared their orbits and “Platonic bodies” while searching for the concealed mathematical harmony of the universe. Kepler was so convinced of his mystical theory that he immediately sent it to the prominent astronomers of the late 16th century, Galileo Galilei and Tycho Brahe. Although they rejected the young man’s fantasy, they acknowledged his originality and intelligence, with Galileo Galilei supporting the young scientist’s dedication to the heliocentric model of the world. This allowed Kepler to enter the scientific community and fearlessly express his ideas. However, one of his ideas was not well-received by Galileo: Kepler argued that Mars moves in an ellipse, not a circle. The concept that all celestial body orbits are ellipses, which is now considered axiomatic, was not immediately accepted by astronomers. At that time, the irregular motion of the Sun, Moon, and planets was explained in a complex manner: it was believed that the planet moved uniformly in a small circle called an epicycle, while the center of the epicycle moved in a larger circle called a deferent.
“I have always admired the intellect of Kepler – keen and unconstrained, maybe even excessively so, but our thought processes differ greatly,” Galileo remarked about Kepler. Tycho Brahe, on the other hand, extended an invitation to the budding astronomer, and they embarked on a decade of fruitful collaboration. The outcome of this partnership is precisely what gave rise to Kepler’s renowned three laws.”
Kepler’s First Law
Brahe’s extensive observations demonstrated that Mars does not orbit in a perfect circle. In his quest to explain this perplexing phenomenon, Johannes Kepler formulated his first law: “Each planet in our solar system follows an elliptical orbit, with the Sun located at one of the foci.”
Kepler’s Second Law
Kepler’s Second Law states that the speed of a planet varies as it travels closer to or further away from the Sun. The velocity of a planet decreases as it moves farther away from the Sun, while it increases when it approaches the Sun.
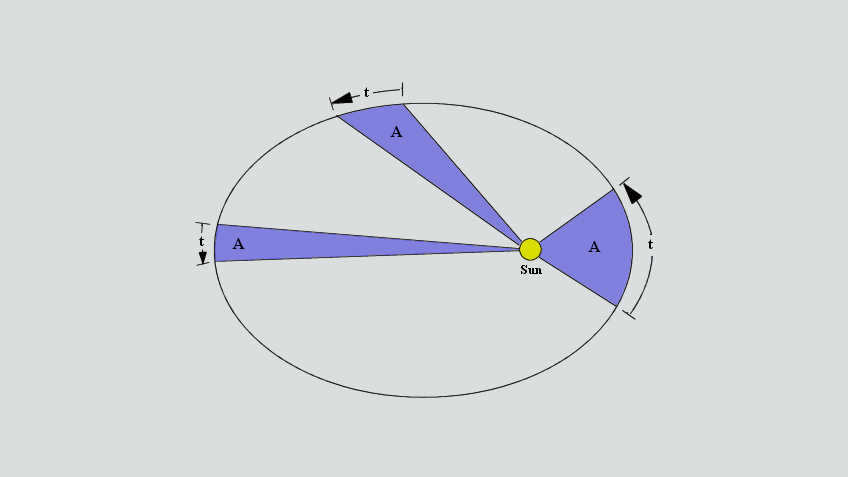
The principle is expressed in the following manner: the radius vector linking a planet and the Sun describes equal areas in equal times. The radius vector is a line connecting the Sun and a planet in orbit around it. To better comprehend this principle, a visual diagram can be of assistance: the shaded areas are equivalent and cover the same amount of time.
Kepler’s Third Law
Kepler’s third law provides a means of determining the velocity of a planet and the duration of its revolution around the Sun. Specifically, it asserts that the squares of the orbital periods of the planets are proportional to the cubes of the major semi-axes of their respective orbits.

T1 and T2 represent the orbital periods of two celestial bodies revolving around the Sun, while a1 and a2 denote the lengths of the major semi-axes of their respective orbits.
The Harmony of the Universe
The mathematical elegance of the cosmos, which scientists have long envisioned, has received an unexpected affirmation: it has been discovered that the ratio between the major and minor radii of all planets in the Solar System remains constant and aligns with the golden ratio, with an error margin of less than one percent.
“I discovered that every movement of the celestial bodies, whether considered as a whole or in each individual case, is infused with a universal harmony, albeit different from the one I had initially imagined, but even more flawless,” Kepler expressed in his writings. Following his breakthroughs, the notion of Earth being the epicenter of the cosmos was ultimately discarded from the field of astronomy.
Despite the significant contribution made by Johannes Kepler to the advancement of science, his mother faced a perilous situation: she was accused of practicing witchcraft in 1615 and was subjected to being shackled to an iron chain at the city gates, awaiting execution for a period of five years. Kepler had to personally take up her defense in court, temporarily setting aside his astronomical pursuits in order to refute a total of fifty charges brought against her, which included allegations of associating with the devil, committing blasphemy, engaging in sorcery, necromancy, and more. Eventually, Kepler’s mother was acquitted of all accusations, but sadly, she passed away six months later in 1621. Kepler continued to live for another nine years and managed to publish his final book, titled “The Harmony of the World.”
Albert Einstein highly praised Kepler’s contribution to science. According to the author of the theory of relativity, Kepler lived in a time when there was no confidence in the existence of a general regularity for all natural phenomena. Despite working alone and receiving no support or understanding, Kepler had a deep faith in such a pattern. For many decades, he drew strength from this belief to conduct difficult and meticulous empirical studies on planetary motion and the mathematical laws governing it. The establishment of these laws required immense ingenuity, imagination, and tireless hard work. It is now difficult to fathom the level of dedication and precision that Kepler demonstrated.
String Theory: The Ultimate Unifying Theory
The Falling Fruit or Originality: Newton’s Journey to Discovering the Law of Universal Gravitation
This website may contain content sourced from online platforms Facebook and Instagram, which are owned by Meta Platforms Inc., a company that is not accessible in the Russian Federation.

Johannes Kepler, a mathematician, astronomer, mechanic, optician, and the one who discovered the laws of motion of the planets in the solar system, was born on December 27, 1571 in Weil der Stadt and died on November 15, 1630 in Regensburg.
1 Life Story
1.1 Early Life
1.2 Residence in Prague
1.3 Final Years
2 Scientific Contributions
2.1 The Field of Astronomy
2.2 Mathematical Endeavors
2.3 Explorations in Mechanics and Physics
2.4 Innovations in Optics
3 Kepler’s Perspective on Astrology
4 Remembering Kepler
5 Additional Information
6 Works by Kepler
6.1 Translations into Russian
7 Reminders
8 Literature
9 References
Biography
Early Life
Johannes Kepler was born in the historic city of Weil der Stadt (30 kilometers from Stuttgart, now in the federal state of Baden-Württemberg). His father, Heinrich Kepler, served as a soldier in the Spanish Netherlands. When Kepler was 18 years old, his father went on another journey and never returned. Kepler’s mother, Katharina Kepler, ran an inn and also worked part-time as a fortune-teller and herbalist.
In 1589, Kepler completed his studies at the Maulbronn monastery school, demonstrating exceptional talent[4]. As a result, he was granted a scholarship by the city authorities to further his education. In 1591, he enrolled at the University of Tübingen, initially studying at the Faculty of Arts, which encompassed mathematics and astronomy at the time, before switching to the theological faculty. It was here that he first learned about Nicolaus Copernicus’ heliocentric system of the world, thanks to Michael Möstlin, and immediately became a staunch advocate for it. One of Kepler’s close friends at university was Christoph Bezold, who would later become a lawyer.
Initially, Kepler had plans to become a Protestant priest, but his exceptional mathematical abilities led to an invitation to lecture on mathematics at the University of Graz (now in Austria) in 1594.
There should be a picture here.
“Kepler’s Cup”: a representation of the celestial system crafted from five Platonic solids.
During his time in Graz, Kepler dedicated six years to his studies. It was during this period that he published his first book, titled “Mystery of the Universe” (Mysterium Cosmographicum), in 1596. In this work, Kepler sought to uncover the enigmatic harmony that governed the Universe. To do so, he compared the orbits of the five known planets (with a particular focus on the Earth’s orbit) to various “Platonic bodies” or regular polyhedrons. For instance, he represented the orbit of Saturn as a circle, not yet realizing that it was an ellipse, on the surface of a ball that was described around a cube. Within this cube, he inscribed another ball, symbolizing the orbit of Jupiter. Inside this ball, Kepler placed a tetrahedron that was described around a ball to represent the orbit of Mars, and so on. Despite the fact that Kepler’s later discoveries rendered this work less significant (particularly because the planets’ orbits were not perfectly circular), he maintained his belief in the existence of a concealed mathematical harmony within the universe until the end of his life. In 1621, he republished “The Mystery of the World,” introducing numerous modifications and additions to the original text.
Galileo and Tycho Brahe received a copy of the book The Mystery of the Universe from Kepler. Galileo was in favor of Kepler’s heliocentric approach, although he did not believe in mystical numerology. They later engaged in an active correspondence, and this fact (the communication with a “heretic” – Protestant) was highlighted as an aggravating factor in Galileo’s trial[7].
Tycho Brahe, like Galileo, rejected Kepler’s elaborate theories, but admired his intellect and originality of ideas and even invited Kepler to his residence.
Kepler and Brahe, who had been banished, met in Prague in 1600. Their time there, lasting a decade, was the most productive period in Kepler’s life.
It quickly became apparent that Tycho Brahe only partially agreed with the astronomical views of Copernicus and Kepler. In order to uphold geocentrism, Brahe proposed a compromise model: all planets, except for Earth, orbit the Sun, while the Sun orbits the stationary Earth (a geo-heliocentric world system). This theory gained immense popularity and served as the main rival to the Copernican world system for several decades[9].
After Brahe passed away in 1601, Kepler assumed his position. The emperor’s treasury was constantly depleted due to ongoing wars, resulting in Kepler receiving infrequent and meager salary payments. To make ends meet, he had to take on additional work as a horoscope-maker. Furthermore, Kepler had to endure a lengthy battle with Tycho Brahe’s heirs, who attempted to strip him of not only the deceased’s other possessions but also the records of astronomical observations. Eventually, they were persuaded to relent[10]
In 1604, Kepler released his findings on the supernova now known by his name.
Kepler and Emperor Rudolf II. Engraving by F. Bulot, 1862
Tycho Brahe, known for his exceptional powers of observation, spent many years meticulously documenting the movements of planets and hundreds of stars. His measurements were far more precise than those of any previous astronomer, thanks to his use of advanced technology and a unique method for correcting observational errors. The systematic approach he took to his work was especially noteworthy.
After studying Brahe’s data for several years, Kepler came to the conclusion that the orbit of Mars is not a circle, but an ellipse, with the Sun located at one of the foci. This discovery is now known as Kepler’s first law. Additionally, his analysis revealed another important finding, known as Kepler’s second law: the radius-vector connecting a planet and the Sun sweeps out equal areas in equal times. This means that as a planet moves farther away from the Sun, its speed decreases.
Kepler formulated these laws in 1609 in his book “New Astronomy”, but he only applied them to Mars as a precaution.
In 1610, Galileo informed Kepler about the discovery of Jupiter’s satellites. Kepler responded to this news with doubt and in a polemical piece titled “Conversation with the Starry Messenger,” he humorously questioned why there would be satellites if there was no one on Earth to appreciate the view. Galileo did not initially believe Kepler’s report. However, after receiving his own telescope, Kepler changed his stance, confirmed the existence of the satellites, and became interested in the theory of lenses. This led to the development of an enhanced telescope and the groundbreaking work Dioptrics.
Albert Einstein referred to Kepler as “an unparalleled individual” and commented on his destiny: In an era when the existence of a general regularity in all natural phenomena was still uncertain, Kepler demonstrated an unwavering faith in such regularity. Despite working alone, without support or understanding from others, he drew strength from this belief for several decades to undertake a challenging and meticulous empirical study of planetary motion and its mathematical laws. In today’s world, where this scientific feat has already been accomplished, it is difficult to fully grasp the level of ingenuity, hard work, and patience required to uncover and precisely articulate these laws.
By the end of the sixteenth century, the field of astronomy found itself caught in a battle between two competing systems: Ptolemy’s geocentric model and Copernicus’s heliocentric model. Detractors of the Copernican system argued that it was no more accurate than the Ptolemaic system in terms of calculation errors. It is important to note that in Copernicus’s model, the planets were believed to move uniformly in circular orbits. However, in order to account for the apparent irregularity of planetary motion, Copernicus had to introduce additional epicycles. While Copernicus had fewer epicycles than Ptolemy, his astronomical tables, which initially showed greater accuracy than Ptolemy’s, eventually deviated significantly from actual observations. This discrepancy puzzled and dampened the spirits of devoted Copernicanists.
Kepler, with great precision and accuracy, completely elucidated the apparent irregularity of planetary motion through the discovery of his three laws. Rather than relying on convoluted epicycles, Kepler’s model simplifies the motion to a single curve – the ellipse. The second law delineates the variation in a planet’s velocity as it distances itself or approaches the Sun, while the third law enables the calculation of said velocity and the period of revolution around the Sun.
Despite being based on the Copernican model historically, the Keplerian world system actually has very little in common with it, except for the daily rotation of the Earth. The circular motion of the spheres carrying the planets has been replaced, and the concept of planetary orbit has been introduced. In the Copernican system, the Earth still held a somewhat special position, as Copernicus declared the center of the Earth’s orbit to be the center of the world. In Kepler’s system, however, the Earth is just an ordinary planet whose motion is governed by the general three laws. All celestial bodies orbit in ellipses (with the discovery of motion along hyperbolic trajectories coming later with Newton), with the Sun being the common focus of these orbits.
Kepler also derived the “Kepler equation”, which is used in astronomy to determine the position of celestial bodies.
Kepler derived his views on the structure of the universe beyond the solar system from his mystical philosophy. In his belief, the Sun was stationary and the sphere of stars marked the boundary of the world. Contrary to the concept of an infinite universe, Kepler proposed the photometric paradox in 1610 as an argument: if the number of stars is infinite, then in any direction, the eye would encounter a star, leaving no dark areas in the sky[23][24].
Kepler’s world system not only aimed to uncover the laws of planetary motion but also sought to reveal something much more profound. Similar to the Pythagoreans, Kepler perceived the world as a manifestation of numerical harmony, both geometric and musical. By unraveling the structure of this harmony, Kepler believed he could answer the most profound questions.
I have discovered that all movements of celestial bodies, both as a whole and in individual cases, are filled with a universal harmony – although not the one I originally assumed, but even more flawless.
As an example, Kepler provides an explanation for why there are precisely six planets (at that time, only six planets in the solar system were known) and why they are positioned in space in this specific manner and not any other: it turns out that the planets’ orbits are enclosed within regular polyhedra. It is fascinating to note that, based on these non-scientific considerations, Kepler made a prediction about the existence of two moons orbiting Mars and an intermediary planet located between Mars and Jupiter.
Kepler’s laws brought together lucidity, simplicity, and computational prowess, yet the enigmatic structure of his planetary system significantly tainted the true essence of Kepler’s groundbreaking discoveries. However, Kepler’s contemporaries were already convinced of the accuracy of these new laws, although their deeper significance remained obscure until Newton’s time. No endeavor was ever made to revive Ptolemy’s model or propose an alternative system of motion that deviated from heliocentricity.
The frontispiece of the Rudolph Tables.
Kepler played a significant role in persuading Protestants to adopt the Gregorian calendar, as demonstrated during the Diet in Regensburg in 1613 and Aachen in 1615.
Kepler was the first to write a comprehensive account of Copernican astronomy in three volumes, known as the Epitome Astronomiae Copernicanae (1617-1622). However, this groundbreaking work was immediately banned and included in the Index of Prohibited Books. In this influential book, Kepler detailed all of his astronomical discoveries.
In 1627, after 22 years of hard work, Kepler self-published astronomical tables known as “Rudolph’s” in honor of the emperor. These tables were in high demand because previous tables had become outdated and were no longer accurate. Notably, Kepler’s tables also included logarithms for easier calculations. Astronomers and sailors relied on Kepler’s tables until the early 19th century.
Following Kepler’s demise, Gassendi witnessed the anticipated event of Mercury passing across the Sun’s surface[26]. In 1665, Italian physicist and astronomer Giovanni Alfonso Borelli released a publication validating Kepler’s laws for the Jupiter satellites that were discovered by Galileo.
Mathematics
Kepler discovered a technique for calculating the sizes of different objects that rotate, as detailed in his renowned book “New Stereometry of Wine Casks” (1615). This groundbreaking method was the first to incorporate integral calculus[27]. Cavalieri later applied a similar approach to create the highly productive “method of indivisibles”. This sequence of advancements ultimately led to the development of mathematical analysis.
During his studies of astronomy, Kepler made significant contributions to the theory of conic sections. Additionally, he was one of the first to compile tables of logarithms[29]. Kepler is credited with coining the term “arithmetic mean” and also played a crucial role in the development of projective geometry by introducing the concept of an infinitely distant point[30]. Furthermore, he introduced the idea of the focus of a conic section and explored projective transformations of these shapes, including the transformation of an ellipse into a hyperbola. Mechanics and physics[edit edit code]
Kepler was the one who first used the term inertia in physics to describe the inherent resistance of bodies to an external force. He also, like Galileo, clearly stated the first law of mechanics: a body that is not acted upon by other bodies is either at rest or moving in a straight line at a constant speed[31].
Kepler came very close to discovering the law of gravitation, although he did not attempt to express it mathematically. In The New Astronomy, he wrote that there is a “mutual tendency of similar bodies to come together or unite” in nature. According to him, this force is caused by magnetism combined with the rotation of the Sun and planets around their axis[32].
In another publication, Kepler provided further clarification[32]: My definition of gravity is a force that resembles magnetism – a mutual attraction. The strength of this attraction increases as the distance between the two bodies decreases.
Kepler mistakenly held the belief that this force only operates within the plane of the ecliptic. He also incorrectly believed that the force of attraction decreases in proportion to the distance (rather than the square of the distance).
Kepler, almost a century before Newton, was the first to propose that the tides were caused by the moon’s influence on the Earth’s upper oceans[33].
In 1604, Kepler released a substantial treatise on the subject of optics called Supplements to Vitellius. This work marked the beginning of optics as a scientific discipline [34]. Kepler’s treatise delved into both geometrical and physiological optics. He discussed the refraction of light, the concept of optical image, and the general theory of lenses and lens systems. He introduced terms such as “optical axis” and “meniscus”, and he was the first to formulate the law of incidence, which states that the intensity of illumination is inversely proportional to the square of the distance to the light source. Additionally, Kepler was the first to describe the phenomenon of total internal reflection, which occurs when light passes from a more dense medium to a less dense one.
Kepler had mixed feelings about astrology. While he acknowledged that there is a harmonious connection between the earthly and celestial realms, he remained skeptical about using this harmony for predicting specific events.
According to Kepler, people are mistaken in believing that earthly affairs are influenced by the celestial bodies. In one of his well-known statements, he also expressed:
Undoubtedly, astrology is a foolish offspring, but, my goodness, where would its noble mother, astronomy, be without this foolish child! Light, after all, is still much more ignorant and foolish, to the point that the foolish child must prattle and lie for the sake of its wise old mother. Furthermore, mathematicians are paid so meagerly that the mother would likely starve if the child earned nothing.
However, Kepler never disassociated himself from astrology. Furthermore, he held his own unique perspective on the nature of astrology, setting him apart from his astrological peers. In his work “Harmony of the World,” Kepler argues that there are no celestial bodies in the sky that bring misfortune. Instead, he suggests that the human soul has the ability to “resonate” with the rays of light emitted by the celestial bodies, imprinting in its memory the configuration of these rays at the moment of birth. According to Kepler, the planets themselves were living beings with distinct souls[36].
Kepler gained a reputation as a skilled astrologer thanks to his successful predictions. While in Prague, one of his responsibilities was to create horoscopes for the emperor. It is worth mentioning, however, that Kepler did not practice astrology solely for financial gain. He also created horoscopes for himself and his family. In his autobiographical work, “About Myself,” Kepler provides a description of his own horoscope. Additionally, when his son Henry was born in January 1598, Kepler made a horoscope for him. According to his analysis, the year 1601 was the closest to when his son’s life would be in danger. However, tragically, his son passed away in April 1598.
Kepler’s attempts to create a horoscope for General Wallenstein were unsuccessful. In 1608, Kepler made a horoscope for the commander, predicting that he would get married in his 33rd year of life and highlighting the life-threatening years of 1613, 1625, and his 70th year. Kepler also described several other events. However, right from the start, the predictions did not come true. Wallenstein returned the horoscope to Kepler, who then adjusted the time of birth by half an hour, leading to an exact match between the prediction and the course of Wallenstein’s life. However, even this corrected version still had errors. For instance, Kepler believed that the period from 1632 to 1634 would be prosperous for the commander and not pose any danger. However, in February 1634, Wallenstein was killed.

At the moment, there are extra savings discounts (ranging from 2% to 25%) that can be availed by 58,741 educational establishments. To determine the specific discount applicable to all staff members of your educational institution, kindly sign in to your personal Infoworks account.


A course for professional retraining
Managing the tasks of a librarian in professional education
In addition to this offer, we can apply a discount based on the affiliation of your educational institution (the discount percentage will depend on the number of colleagues from your institution who have already completed Infoworks courses).
Currently, 58,741 educational institutions are eligible for additional discounts ranging from 2% to 25%. To find out the specific discount available to all employees of your educational institution, please log in to your personal Infoworks account.


Enroll in our professional retraining course
Master the art of managing electronic services for archives, libraries, and information-library centers.
We offer the opportunity to apply your educational institution’s discount to our course fees. The amount of the discount depends on the number of your colleagues who have previously enrolled in Infoworks courses.
Currently, there are 58,741 eligible educational institutions that can benefit from additional cumulative discounts ranging from 2% to 25%. To find out the specific discount available to all employees of your educational institution, simply log in to your personal Infoworks account.


Creating a Personal Brand through Publications and Media Outreach
Overview of the Presentation


One thing that never fails to fill the soul with increasing wonder and awe the more we contemplate it, is the vast expanse of the starry sky above us.

Slide 3 The laws of planetary motion –
Kepler’s laws
The laws of planetary motion –
Kepler’s laws

Slide 6 Kepler’s Law of Orbits
The planets revolve around the Sun in elliptical paths, with the Sun located at one of the foci of the ellipse.
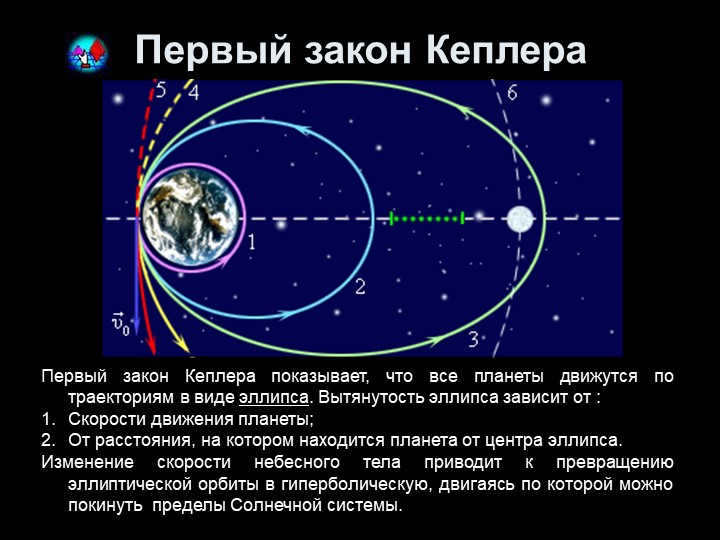
Kepler’s First Law is a fundamental principle that states that the paths of all planets can be described as ellipses. The shape of the ellipse is determined by two factors: the speed at which the planet is moving and its distance from the center of the ellipse. If the velocity of a celestial body changes, its elliptical orbit can transform into a hyperbolic orbit, allowing it to potentially escape the confines of the solar system.
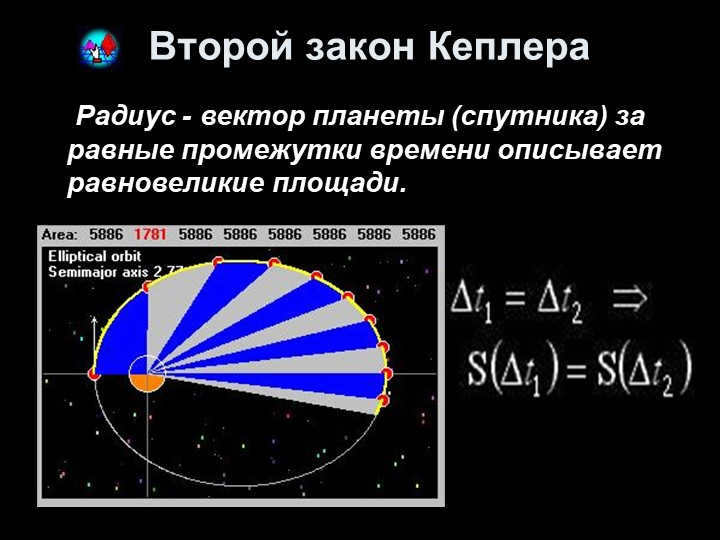
The second law of Kepler states that the planet’s (satellite’s) radius vector covers equal areas in equal time intervals.


Slide 10: Kepler’s Third Law states that the periods of revolution of the planets around the Sun are related to each other in a unique way. Specifically, the squares of these periods are proportional to the cubes of the major semi-axes of their orbits.

Planetary configurations play a crucial role in determining the positions of the planets in relation to both the Earth and the Sun, ultimately influencing their visibility in the sky. Each planet emits a radiant glow, courtesy of the Sun’s reflected light. Consequently, the planet that is closest to the Earth is generally the most visible, assuming that its sunlit side is facing us during the daytime.
Illustrated in Figure 4.1 is the opposition (OA) of Mars (M1), a specific configuration in which the Earth aligns in a straight line between Mars and the Sun. During the opposition, the planet appears at its brightest as its entire sunlit hemisphere is directly facing the Earth.
The paths of the two planets, Mercury and Venus, are nearer to the Sun than that of the Earth, resulting in them not being in opposition. When Venus or Mercury are at their closest point to the Earth, they cannot be seen as the side of the planet facing away from the Sun is in darkness (Fig. 4.1). This arrangement is referred to as a lower conjunction with the Sun. Similarly, during an upper conjunction, the planet is not visible due to the presence of a bright Sun between it and the Earth.
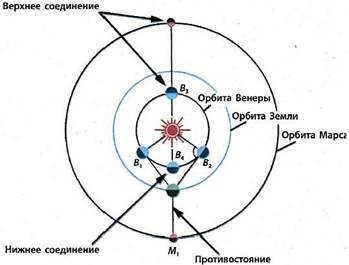
Figure 4.1. Venus and Mars Configurations. Mars opposition – when the planet is closest to Earth, it can be seen throughout the night in the opposite direction from the Sun. Venus is most visible in the evening during its eastern elongation, appearing to the left of the Sun (B1), and in the morning during its western elongation, appearing to the right of the Sun (B2).
Opposition refers to when a planet is visible from Earth throughout the night in the opposite direction from the Sun.
Elongation is the angular distance between a planet and the Sun as observed from Earth’s surface.
The most favorable conditions for observing Venus and Mercury occur during specific configurations known as elongations. The planet is considered to be in eastern elongation when it is visible in the evening sky to the left of the Sun. On the other hand, the western elongation of Venus can be observed in the morning when the planet is visible to the right of the Sun in the eastern part of the sky.
There are different symbols used to represent the positions of these planets. Opposition refers to when the planet is visible throughout the entire night, while conjunction with the Sun means that the planet is not visible. Eastern elongation indicates that the planet can be seen in the evening in the western part of the horizon, whereas western elongation signifies that the planet is visible in the morning in the eastern part of the sky.
The motion of celestial bodies in relation to the stars is determined by the sidereal orbital period. This refers to the amount of time it takes for a planet to complete one full revolution around the Sun while moving in its orbit (Fig. 4.2).
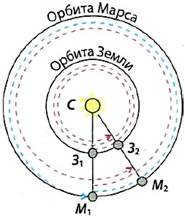
Fig. 4.2. The blue dotted line represents the path of Mars’ orbit around the Sun corresponding to its sideric period, while the red dotted line represents its synodic period
The synodic period determines the motion of celestial bodies relative to the Earth and the Sun. It is the duration during which the same successive configurations of the planets (opposition, conjunction, elongation) are observed. In Fig. 4.2, the positions of NW1-М1 and C-32-М2 represent two consecutive oppositions of Mars. The synodic S and sideric T periods of the planet’s orbit are related as follows: (4.1)
Kepler’s Laws
Johannes Kepler (Figure 4.3) discovered that the movement of Mars around the Sun occurs in an elliptical path, and subsequent research confirmed that other planets also follow elliptical orbits.
Kepler’s first law states that all planets revolve around the Sun in elliptical paths, with the Sun positioned at one of the foci of these ellipses (Figures 4.4, 4.5).
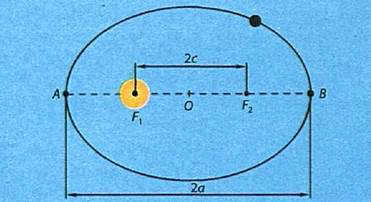
Figure 4.4. The planets revolve around the Sun in elliptical orbits. AF1=Fmin – at the point of closest approach; BF1=Fmax – at the point of farthest distance
The primary implication of Kepler’s first law is that the distance between the planet and the Sun is not fixed and fluctuates within the range: rmax ≤ r ≥ rmin
The Earth reaches its closest point to the Sun, known as perihelion, on January 3-4, when it is approximately 147 million km away.
Conversely, the Earth is at its farthest point from the Sun, known as aphelion, on July 3-4, when it is approximately 153 million km away.
Kepler’s Second Law. According to this law, a planet’s radius-vector traces out equal areas in equal time intervals.
One of the main implications of Kepler’s second law is that as a planet orbits the Sun, not only does its distance from the Sun change over time, but also its linear and angular velocity.
The planet reaches its highest velocity at perihelion, when it is closest to the Sun, and its lowest velocity at aphelion, when it is farthest from the Sun.
Kepler’s second principle, in fact, establishes the renowned principle of energy conservation: the total energy (kinetic and potential) in a closed system remains constant. The velocity of a planet determines its kinetic energy, while the distance between the planet and the Sun determines its potential energy. Therefore, as the planet approaches the Sun, its velocity increases (Fig. 4.6).
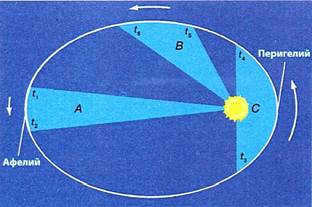
Figure 4.6. The planet’s speed increases when it approaches the Sun, and decreases when it moves away.
If it is difficult to verify the first law of Kepler in a school setting, which requires measuring the distance from Earth to the Sun in both winter and summer, the second law of Kepler can be easily tested by any student. To do this, one simply needs to observe that the speed of Earth changes throughout the year. This can be done using a regular calendar and calculating the duration of the half-year from the spring equinox to the autumnal equinox (March 21st to September 23rd) and vice versa, from September 23rd to March 21st. If Earth orbited the Sun at a constant speed, the number of days in these half-years would be the same. However, according to Kepler’s second law, Earth’s speed is greater in winter and slower in summer. Therefore, summer in the Northern Hemisphere is slightly longer than winter, while in the Southern Hemisphere, winter is slightly longer than summer.
The Earth’s minimum speed during the summer is 29.36 km/s.
In the month of July, the Earth’s speed decreases, resulting in a longer summer in the Northern Hemisphere compared to the Southern Hemisphere. This is why the average annual temperature in the Northern Hemisphere is higher than in the Southern Hemisphere.
Kepler’s Third Law. The squares of the sidereal periods of the planets’ orbits around the Sun are proportional to the cubes of the major semi-axes of their orbits.
Let T1 and T2 represent the sideric period of orbital motion for any planets, and represent the major semi-axes of the orbits of these planets.
By determining the major semi-axis of the orbit for any planet or asteroid, one can use Kepler’s third law to calculate the orbital period of this celestial body without having to wait for a full revolution around the Sun. For instance, in 1930, a new planet named Pluto was discovered in the Solar System, which has a major semi-axis of 40 astronomical units (a.e.). Consequently, the orbital period of Pluto around the Sun was determined to be 248 years. However, in 2006, the International Astronomical Union Congress reclassified Pluto as a dwarf planet due to its orbit intersecting with that of Neptune.
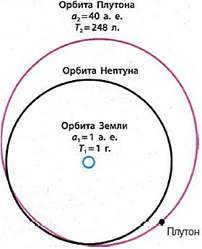
Figure 4.7. The determination of Pluto’s orbit major semi-major axis was made through observations. By considering the parameters of Earth’s orbit as stated in 4.2, we find T2 = 248 years.
Kepler’s third law is also applicable in astronautics for calculating the orbital period of satellites or spacecraft around Earth.
Newton’s Law of Universal Gravitation
Isaac Newton, the renowned physicist and mathematician from England, established the scientific principle behind Kepler’s laws, known as Newton’s Law of Universal Gravitation. This law not only governs the movement of planets within the solar system but also governs the interaction between stars in the Galaxy. In 1687, Newton formulated this law, stating that any two objects with masses M1 and M2 are attracted to each other by a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them (see Figure 4.8):
The distance between these bodies is denoted by R, while the gravitational constant is represented by G.
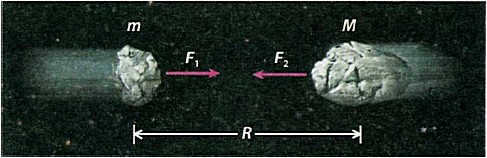
Figure 4.8. The Law of Universal Gravitation
It is important to note that equation (4.3) is only applicable to two individual points. However, if a celestial body has a spherical shape and its density is symmetrically distributed around its center, then the mass of the body can be treated as a single point located at the center of the sphere. For instance, when a spaceship orbits the Earth, the distance from the center of the Earth is used to calculate the gravitational force between the Earth and the spaceship (Fig. 4.9).
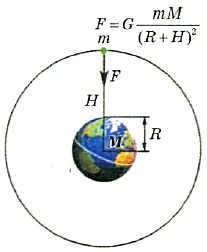
Figure 4.9. The gravitational force experienced by a spacecraft is determined by the distance R+H between the spacecraft and the center of the Earth
By utilizing equation (4.3), it becomes possible to calculate the weight of astronauts on any given planet, given the values of its radius R and mass M (Fig. 4.10). According to the law of universal gravitation, not only is a planet attracted to the Sun, but the Sun is also attracted to the planet with the same magnitude of force. As a result, the motion of both bodies within the gravitational field occurs around the system’s common center of mass. This means that the planet does not fall into the Sun because it is in orbit around the planet at a specific velocity, and similarly, the Sun does not fall towards the planet due to the force of gravity, as it too orbits around the common center of mass.
The mass of the planet and its radius are determining factors for the weight of astronauts. On asteroids, astronauts have to secure themselves with tethers to prevent them from drifting off into space.
In actual conditions, planets do not move in elliptical orbits as Kepler’s laws only apply to two bodies orbiting around a common center of mass. In the Solar System, large planets and numerous small bodies orbit around the Sun, causing each planet to be influenced not only by the Sun but also by the gravitational pull of these other bodies. This results in a complex motion for each planet due to the varying magnitudes and directions of these forces. This type of motion is known as perturbation. The path along which a planet moves during perturbation is not an ellipse.
Conclusions
All celestial objects, ranging from planets to galaxies, follow the principles of universal gravitation, which were first discovered by Newton. Kepler’s laws govern the shape of their orbits, the velocities at which they move within the solar system, and the duration of their revolutions around the sun.
Tests
A. Configuration.
B. Opposition.
C. Cosmogony.
D. Ascension.
E. Displacement.
F. Saturn.
G. Venus.
H. Mercury.
I. Jupiter.
J. Saturn.
K. Venus.
L. Mercury.
M. Jupiter.
N. Leo.
O. Capricorn.
P. Orion.
Q. Pisces.
R. Aquarius.
S. Perihelion.
T. Perigee.
U. Apogee.
V. Aphelion.
W. Apex.
- At what time can Mars be observed throughout the entire night?
- Is Venus visible when it is closest to Earth?
- During which time of year does Earth have its highest orbital velocity?
- Even though Mercury is brighter than Sirius, why is it difficult to see in the sky?
- Is it possible to see Earth from the surface of Mars during the Mars opposition?
- If an asteroid has a period of 3 years and is 3 a.e. from the Sun at aphelion, could it collide with Earth?
- Can a comet exist in the Solar System if it has a 100-year period and passes near Neptune at aphelion?
- How can the weight of astronauts on any planet be calculated if the planet’s radius and mass are known?
Tasks related to observations
Using an astronomical calendar, find out which planet in our solar system is closest to Earth on your birthday this year. Also, identify the constellation in which it can be observed tonight.
Important concepts and terms:
Aphelion, elongation, planetary configurations, parallax, perihelion, opposition, sideric and synodic period.
1. Astronomy. Basic level. Grade 11: textbook / B. A. Vorontsov-Vel’yaminov, E. K. Straut. – 5th ed., revision. – Moscow: Drofa, 2018.
2. Astronomy. 11th grade. Methodical manual for the textbook B. A. Vorontsov-Veliaminov, E. K. Straut “Astronomy. Basic level. 11th grade” / M. A. Kunash. – M .: Drofa, 2018.
3. N.N. Gomulina. Open Astronomy / Edited by V.G. Surdin. – Electronic educational resource. http://www.college.ru/astronomy/course/content/index.htm




