Who is the scientist who discovered the laws of motion? - Explore the Universe: Your Guide to Astronomy

Johannes Kepler, a renowned German mathematician, astronomer, and astrologer, is celebrated for his insatiable thirst for knowledge, unwavering dedication to research, and remarkable endurance. His writings continue to be revered and admired.

Together with Newton and Galileo, Kepler is considered one of the most influential scientists of the Renaissance era. He served as an astrologer to Rudolph II, the king of the Holy Roman Empire, and gained recognition in scientific circles for his groundbreaking “Keplerian” laws of planetary motion.

Biography and scientific activity

Johannes Kepler (December 27, 1571, Weil der Stadt – November 15, 1630, Regensburg) was a German mathematician, astronomer astrologer, and optician. He made groundbreaking discoveries in the field of planetary motion.

Born in Weil der Stadt, a suburb of Stuttgart, Kepler’s father was a salaried military man and his mother was a housewife. At the age of 17, his father abandoned the family, leaving Kepler to care for his seriously ill mother. Throughout his childhood and adolescence, Kepler faced numerous challenges, including a lack of proper care and frequent bouts of poor health, which made him susceptible to extended periods of illness.

Kepler’s fascination with astronomy was sparked during his early years, when his mother Katharina Kepler introduced him to comets and a lunar eclipse (1580). After completing school at the Maulbronn monastery in 1589, he enrolled in the theological faculty of the University of Tübingen in 1591, where he was first exposed to the concepts of Nicolaus Copernicus. Initially, Kepler had aspirations of becoming a Protestant clergyman, but his proficiency in mathematics led to an invitation in 1594 to teach mathematics at the University of Graz.

Kepler and his wife were forced to leave Graz in 1600 due to conflicts with the Catholic Church. They were invited to Prague by astronomer Tycho Brahe, where they faced challenges in their collaborative work. Although Copernicus and Kepler had similar views on astronomy, Tycho Brahe had only partial agreement with them. Despite this, Brahe was an exceptional observer and had compiled a comprehensive descriptive work on planets and stars, lacking mathematical analysis.

Following Brahe’s passing in 1601, Kepler takes over his position as the royal mathematician and astronomer. In 1604, Kepler publishes his own new observations.

In 1611, Kepler released Dioptrica, marking the inception of optics as a scientific discipline. In this seminal work, Kepler meticulously elucidates the phenomenon of light refraction and introduces the concept of the optical image. Possessing an extraordinary grasp of these intricacies, Kepler went on to conceive the blueprint for a revolutionary telescope, which was subsequently constructed by Christoph Scheiner in 1613.

After the Kaiser of Prague passed away in 1612, Kepler relocated to Linz. Further examination of Mars’ orbit led Kepler to make a groundbreaking discovery in 1618: the third law. This law states that the ratio of a planet’s distance from the Sun cubed to the period of its revolution around the Sun squared is constant for all planets: a³/T²=const. Kepler documented this finding in his publication, The Harmony of the World.

Despite the challenges he faced throughout his life, especially during his final decade, Kepler managed to publish his most influential work in 1621: Epitome Astronomiae. This publication discussed heliocentric astronomy and left a lasting impact.

After twenty years of work, Kepler finished the planetary tables that Tycho Brahe had started long ago. These tables, known as Rudolph’s Tables, were published in Ulm in 1627.

One significant event in the scientific community was Kepler’s prediction of Venus passing in front of the sun in 1631. This prediction was based on the laws he had discovered.

Isaac Newton later built upon Kepler’s laws of planetary dynamics to develop his theory of gravity.

In addition to his works on astronomy, Kepler authored several other fascinating publications. One of these included a method for determining the volumes of objects, which contained the initial principles of integral calculus. Furthermore, Kepler meticulously analyzed the symmetry of snowflakes. His examination of symmetry led him to propose the concept of dense packing of spheres, which suggests that the highest packing density is achieved when spheres are arranged in a pyramidal fashion. The mathematical foundation of this theory remained unproven for the next four centuries. The first documentation of a proof emerged in 1998 in a publication by mathematician Thomas Hales, although the final verification of his computer-generated proof is still pending. Kepler’s groundbreaking research on symmetry later found practical applications in fields such as crystallography and coding theory.

Research conducted by Kepler

Kepler initiated his research activities fifty years prior to the announcement of Copernicus’ Hypothesis “on the deceptive motion of the planets” in 1543. Kepler’s theory diverged from the long-standing Ptolemaic geocentric model, which had been in effect for over two millennia. The most audacious proposition of his hypothesis was the displacement of Earth from the center of the universe and the placement of the Sun at said center, with Earth being one of the planets moving in a perfectly circular orbit. Despite Nicolaus Copernicus simplifying the mechanism of celestial body motion with this reform, he still couldn’t completely detach himself from certain key aspects of the geocentric principle of planetary motion, such as the planets’ circular motion at a constant speed. Since the time of Pythagoras in the 6th century BC, the circle had been regarded as perfect, with the planets moving in circular orbits at the same speed. The notion that they could move faster or slower at certain points in their journey was deemed highly inappropriate and unseemly. This notion was later embraced by Christians and was also fully accepted by Kepler’s contemporaries Tycho Brahe and Galileo, thus becoming an integral part of education. The existence of this theory is apparent in the fact that even Nicolaus Copernicus himself, who managed to shift Earth from the center of the universe, couldn’t fathom that the planets could move in any way other than a perfect circle. Copernicus even once suggested that “the mind struggles to conceive of an alternative possibility for the motion of celestial bodies, as it would be simply unworthy to imagine anything that contradicts the most perfect manner – circular motion with constant velocity.” (“Cosmos” by Carl Sagan)

In the meantime, there existed a fundamental and crucial distinction between the Pythagoreans and Kepler. Unlike modern science, which relies on experimentation and observation, Pythagoras taught that the laws of nature could be derived through pure contemplation. On the other hand, Kepler, as a theorist, depended on the findings of observation, and the most precise observations of the planets’ deceptive movement came from a man named Tycho Brahe. Even before the birth of this renowned astrologer, tables detailing the position and motion of the planets (from a geocentric perspective) had been compiled. However, the data in these tables indicated significant deviations from reality. Tycho Brahe refined both the astrological instruments and the observations themselves. He was an exceptional observer and, with his instruments, achieved accuracies down to one lunar minute.

Kepler’s understanding

After a few years, due to pressure from the Lutheran Church, Kepler traveled to Prague in 1600 and joined the renowned Danish astronomer Tycho Brahe, who was then working as a mathematician (astrologer) for King Rudolf II. When Tycho Brahe passed away, Kepler took over his position.

Kepler analyzed Tycho Brahe’s observations of various planets, particularly Mars. Despite not having a telescope, Tycho Brahe was an exceptional observer and had made accurate measurements for two decades. Kepler developed his laws of planetary motion by mathematically interpreting Tycho Brahe’s precise observations.

Brahe also influenced Kepler to focus more on Mars, as its natural movement appeared to be the most irregular and deviated the most from a circular orbit.

Having had the chance to observe the movement of Mars, Kepler started working on mathematically explaining the theory that the Earth and Mars orbit the Sun in rounded paths. After three years of continuous efforts to find proof, Kepler eventually admitted that his concept of the planets’ movement was merely self-deception. He ultimately comes to the conclusion that the universe is organized in a logical manner, but that this “logic” must align with empirical evidence. It took Kepler two more years of research to establish that Mars orbits the Sun in an elliptical trajectory rather than a circular one.

Kepler’s conclusions invalidated the ancient theory that had been in existence for two millennia. Copernicus, on the other hand, hesitated to publish his work for thirty years out of fear that it would disrupt people’s understanding of the world, as it proposed that the Earth was not at the center of the universe but rather one of the planets. By challenging the long-held belief in the Pythagorean theory of celestial motion, Kepler revolutionized the way reality was perceived. In a letter to his friend David Fabricius in 1605, Kepler expressed his apprehension towards his discovery: “I must admit that this elliptical shape scared me. It contradicted the dogma of circular motion that all astronomers have held since the inception of our science. Who am I to dare change the world?”

Kepler revolutionized our understanding of reality, and as Carl Segan famously said, he “ignited the scientific revolution.” In his own words, Kepler wrote:

“We are living in an extraordinary and marvelous era, as our perception of the natural world undergoes profound transformation. However, it is important to remember that it is our perspective that is evolving and expanding, not the actual nature of things themselves.” (Excerpt from a letter to Professor D. A. Madini of Bolony, Prague, September, 1610).

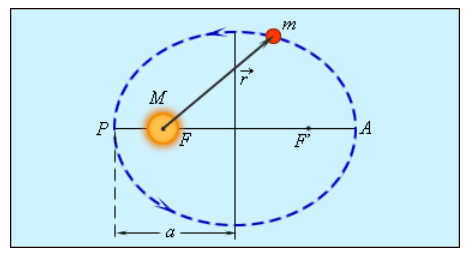
I Kepler’s Law states that the path of any celestial body, such as a planet, follows an elliptical orbit with the Sun at one of the foci.

II Kepler’s Law states that the imaginary lines connecting the planets and the Sun, known as the thrust or radius-vector, sweep out equal areas in equal amounts of time. This implies that planets closer to the Sun move at a faster speed than those that are farther away.

III Kepler’s Law states that the square of a planet’s orbital period is proportional to the cube of its average distance from the Sun.

Kepler’s laws are based entirely on observation and are derived from empirical data. Kepler spent approximately eight years conducting extensive calculations in order to formulate the law of areas. The speed at which a planet orbits is directly related to its proximity to the Sun. At the beginning of each year in January, the Earth accelerates as it passes through perihelion, causing the Sun to appear to move faster along the ecliptic compared to its average annual movement. Conversely, in early July, when the Earth reaches aphelion, its movement slows down, resulting in a deceleration of the Sun’s movement along the ecliptic. The law of areas states that the force governing the orbital motion of the planets is directed towards the Sun.

It is worth remembering that the nature of the gravitational force was mathematically unraveled by the renowned scientist Isaac Newton, who applied Kepler’s Third Law. Although Newton did not explicitly mention his debt to Kepler in his main work “Principia,” he did acknowledge it in a letter to Edmund Haley in 1686, stating, “I admit that I derived this from Kepler’s theory twenty years ago.”

ACHIEVEMENTS, PUBLISHED LITERATURE:

* Mysterium cosmographicum ("Cosmographic Mystery") (1596)
* The more certain foundations of astrology (1602).
* Astronomiae Pars Optica (1604) *
* De Stella nova in pede Serpentarii (On the New Star in Ophiuchus's Foot) (1604)
* Astronomia nova (New Astronomy) (1609)
* Dioptrice (1611).
* Epitome astronomiae Copernicanae ("Abridgment of Copernican astronomy", in three parts) (1618-1621)
* Harmonicse Mundi (1619)
* Tabulae Rudolphinae ("Rudolphine Tables") (1627)
* Somnium ("Sleep")(1634) is a fantasy novel that was published after his death. In this novel, the protagonist embarks on a lunar journey within a dream. In this work, Kepler provided a rather precise depiction of the moon’s surface.

In addition to these renowned works, Kepler also produced a vast array of publications covering various subjects.

Kepler’s impact on the advancement of astrology was significant. He was responsible for establishing the criteria that defined astrology as a legitimate science. According to Kepler, astrology needed to meet three conditions in order to be considered a true science: it had to be grounded in a well-defined philosophical and astronomical cosmogony, it had to have a reliable experimental foundation, and it had to be able to validate the truth of its statements through practical application. Drawing inspiration from Pythagorean traditions, Kepler believed that the universe was founded upon harmonic ratios. For approximately three decades, he dedicated himself to the pursuit of uncovering the universal law of harmony that governed the world.

Kepler also mentioned the correlation between the distances of planets and musical tones in the diatonic scale, with the possibility of transitioning to the chromatic scale if the number of planets (including the Sun and the Moon) reaches twelve. This concept by Kepler foreshadowed the modern concept of quantized planetary orbits. Kepler referred to this as the “music of the spheres,” which he believed could only be heard by the Sun, who acted as the conductor of the entire orchestra known as the Solar System. This idea is presented in Kepler’s work, Mysterium Cosmographicum.
(“The Cosmographic Mystery,” 1596).

Kepler discovered a mathematical connection between the distances of the planets from the Sun and the dimensions of regular polyhedra that are enclosed in a sphere. Currently, scientists are actively considering the concept of the solar system’s pseudo-crystallinity. One of Kepler’s most famous works is Astronomia nova
(New Astronomy, 1609).

During his time, Kepler held a unique perspective that differed from many astrologers. He believed that the planetary influences had no direct impact on a person’s life or destiny. Instead, he argued that these influences merely corresponded to the vibrations or biorhythms of the individual, including their soul. In an attempt to establish astrology on a more reliable and calculable basis, Kepler embarked on an enormous project to calculate ephemerides. This work was eventually published as the “Tabulae Rudolphinae” or “Rudolphine’s Tabulae” in 1627, also known as the “Rudolphine Tables”.

Kepler’s objective was to revolutionize astrology by conducting experimental research, and he dedicated his life to this pursuit. He diligently compiled horoscopes and prognostics, and meticulously verified their accuracy. One of his most notable achievements was the compilation of a horoscope for the renowned general Wallenstein, whom he served as a personal astrologer from 1628 to 1630. Based on this horoscope, Kepler accurately predicted the general’s death, a prediction that was later utilized by Schiller in his play The Death of Wallenstein. Kepler initially gained fame as a remarkable astrologer with his successful astrological predictions in 1595. However, he remained highly skeptical of the predictive astrology prevalent during his time, attributing its flaws to the arbitrary nature of domination systems.

In the biographical literature on Kepler, it is often stated that despite not believing in astrology, Kepler sometimes had to create horoscopes for a living. However, this perspective fails to explain the fact that Kepler also engaged in serious astrological research and conducted a thorough examination of his own horoscope.

The primary focus of Kepler’s astrological research was on aspects. He introduced three minor aspects into astrological practice – quintile (72°), bi-quintile (144°), and sexti-square (135°). Kepler acknowledged the possibility of other combinations but chose to limit himself to these three additional aspects to avoid confusion in practical application.

Kepler’s new ideas were based on the theory of harmony and were supported by empirical observations of astrological effects. After years of experience, research, and analysis of 800 horoscopes, Kepler concluded that the Earth is a living entity with its own soul.
He strongly believed that aspects were the most important factors in astrology. In a brief statement, he wrote:

“Experience is what truly validates the significance of aspects. This is evident to anyone who is not personally convinced of it.”
(excerpt from a letter to Herwart and Feselius; date unknown)

"In my perspective on astrology, I perceive the sky as having a profound influence on individuals, although the exact nature of this influence remains a mystery. I strongly believe that the planetary configurations, known as aspects, play a significant role in shaping people’s lives."
(From Kepler, by Džona Banvila)

Meanwhile, Kepler argues that there are no inherently good or bad aspects, and the planets do not dictate a person’s entire being. The planets do not possess their own agency to determine an individual’s fate, but they do impart a certain character to the soul. Each person, at the onset of their life, absorbs the character and essence of all the constellations in the sky, as well as the energy transmitted through the rays that reach Earth, which remains within them until death.

Kepler hypothesized that the Earth’s atmosphere was susceptible to the influence of other planets. One example of this was the conjunction of Saturn and the Sun, which he believed could result in colder weather. Kepler also drew a parallel between the way human souls can be affected by geometric relationships between planets and the idea that the Earth itself has a soul that is influenced by these planetary aspects, causing changes in the weather.

After years of studying weather patterns and their connection to planetary configurations, Kepler came to the conclusion that specific aspects between planets create a resonance that ultimately leads to changes in weather patterns.

Starting in 1593, Kepler commences documenting the daily weather conditions in Graz, in an attempt to discover a rationale for the correlation between celestial bodies and the climate. Ephemerides II (the second installment), covering the years 1621 and 1629, encompasses Kepler’s detailed records of his daily observations from 1617 to 1620. Furthermore, his calendar spanning from 1617 to 1624 also encompasses a meteorological forecast.

Kepler’s personal understanding of his horoscope

(extract from Kepler’s autobiographical essay, penned in Latin in 1597, at the age of twenty-five, and never intended for publication)

Mercury in the seventh house signifies both swiftness and laziness, as it is associated with speed. The Sun in a harmonious aspect with Saturn indicates both immediacy and endurance. These two qualities are contradictory within individuals: a constant lamentation for wasted time and a constant squandering of time, for which one can only blame oneself. Mercury invokes a devotion to humor and play, which arise from a delight in superficial matters. During my childhood, I wholeheartedly engaged in play, but as I entered young adulthood, my interests shifted and I dedicated myself to other pursuits. This raises the question of what brings pleasure to human beings. Meanwhile, due to my greed, I often played alone. It is important to note that my greed did not stem from a desire to accumulate wealth, but rather from a fear of poverty – although it is possible that all possessiveness stems from a misdirected inclination. The pursuit of money often enslaves many individuals. I have always considered self-interest and honesty in my actions. It is possible that much of this is rooted in a fear and shame surrounding poverty. I am not someone who despises public opinion, but there are times when my words may seem harsh.

For instance, when Saturn aligns with Mercury, it causes a decrease in temperature and dulls the mind. Conversely, when Jupiter aligns with Mercury, it creates warmth. In the former scenario, everything is focused on the desire for accumulation, while in the latter scenario, everything is directed towards the desire for fame and honor. If Mars is observed from its alignment, it appears intimidating. Mars is responsible for mental chaos, frenzy, fickleness, wars, exaggerations, lack of courage, obsession with work – all of which are characteristic of mortal beings. Mars leads to conflict, struggle, acceptance of any order, and criticism of tradition. All the aspects I wish to analyze are brought to the surface. Engaging in heated conversations, arguments, contempt, and fostering immoral habits in certain individuals.”

List of upcoming events at the Kepler Institute – click for the complete list

19.08.2023 ONLINE WEBINAR 20:00 – 21:00

“Kepler’s Laws” – this phrase is well-known to astronomy enthusiasts. Who was Johannes Kepler and what did he discover about the connection and interdependence of the planets’ motion? Kepler, a renowned astronomer, mathematician, theologian, and philosopher, was the genius behind the laws that describe the motion of the solar system’s planets.

The start of the journey

Johannes Kepler, born in December 1571 in Weil der Stadt, Germany, entered this world with various challenges. Despite being weak and visually impaired, he overcame all obstacles to achieve great success in life. His educational journey began in Leonberg, where his family relocated. He then enrolled in a prestigious Latin school to gain a strong foundation in the language, which he would later utilize in his future publications.

In 1589, he completed his studies at the Maulbronn monastery school in Adelburg. In 1591, he enrolled in the University of Tübingen. The dukes implemented a successful educational system during the rise of Lutheranism. They offered grants and scholarships to help less fortunate individuals apply to universities, with the goal of producing well-educated clergy capable of defending the new faith during times of intense religious debates.

During his time at the institution, Kepler was influenced by astronomy professor Michael Möstlin. Möstlin secretly held the same views as Copernicus on the idea of a heliocentric universe, with the Sun at the center. However, he taught his students in accordance with Ptolemy’s geocentric model, with Earth at the center. Kepler’s extensive knowledge of Copernicus’ ideas sparked his interest in astronomy. This meant that Copernicus’ theory gained another supporter, someone who wanted to personally understand the laws of planetary motion around the Sun.

Oddly enough, the individual who ultimately uncovered the laws governing the motion of celestial bodies did not identify himself as an astronomer by profession. Kepler maintained a belief throughout his life that the solar system was a masterpiece teeming with enigmatic phenomena, and he aspired to become a priest. The astronomer justified his fascination with the Copernican theory by asserting that, prior to drawing any conclusions from his own investigations, he must first familiarize himself with various perspectives.

However, university professors regarded Kepler as an exceptionally intelligent student. In 1591, after obtaining his master’s degree, the scholar continued his theological studies. As he was nearing completion, news broke out that a mathematics professor at the Lutheran school in Graz had passed away. The University of Tübingen then recommended the hiring of a talented alumnus for the position. Thus, were the laws of planetary motion left behind?

In the name of the Almighty

Johann, a young man of 22 years old, reluctantly abandoned his original calling to become a clergyman. However, he dutifully took on the role of a mathematics professor in Graz. While delivering a lecture to his students, the inexperienced teacher was sketching geometric shapes on the blackboard, specifically focusing on concentric circles and triangles. Suddenly, a thought crossed his mind – these figures exhibit a consistent ratio between the sizes of two circles, as long as the triangle is equilateral. This led him to ponder the ratio of the areas between two circles. His thought process began to gain momentum.

A year later, this exceptional theologian published his first work, titled “The Enigma of the Cosmos” (1596). Within its pages, he expounded upon his innovative ideas about the mysteries of the universe, all of which were firmly grounded in his religious convictions.

The laws of planetary motion were discovered in the name of God by a researcher who revealed the mathematical plan of the universe. The researcher concluded that there are six planets enclosed in spheres, with five regular polyhedrons fitting between them. However, this version was based on the assumption that there are only six celestial bodies. Kepler proposed the existence of a perfect dodecahedron around the Earth’s orbit and a sphere touching the orbit of Mars.

A tetrahedron and a sphere were observed by the scientist in the vicinity of Mars, located next to the orbit of Jupiter. In the orbital sphere of Earth, the sphere of Venus perfectly fitted into the icosahedron. The same was done with the remaining types of perfect polyhedra. Astonishingly, the ratios of neighboring planetary orbits found in Kepler’s nested model of the spheres coincided with Copernicus’ calculations.

When discovering the laws of planetary motion, a priest with a mathematical mind primarily relied on divine inspiration. He had no concrete basis for his arguments. The significance of the treatise “Mysteries of the Universe” lies in the fact that it was the first major step towards the acceptance of Copernicus’ heliocentric system of the world.

Contrasting Assumptions and High Precision

In September 1598, the Catholic rulers in Graz, Austria expelled Protestants from the city, including Kepler. Despite being permitted to come back, the atmosphere remained highly charged. In search of assistance, Kepler sought out Tycho Brahe, a renowned mathematician and astronomer in the service of Emperor Rudolf II. Brahe was famous for his extensive compilation of planetary observations.

He was aware of the book titled The Enigma of the Cosmos. However, when his creator came to the Tycho Observatory just outside Prague in 1600, Brahe, who was deeply engrossed in his remarkably precise (for that era) research, greeted him as the author of a specific work, but not as a fellow scientist. The confrontation between them persisted until the death of the Danish astronomer, which occurred a year later. Following the departure of his adversary to the afterlife, Kepler was entrusted with safeguarding the treasure trove of Brahe’s observations. These observations proved invaluable in guiding the researcher towards his eventual discovery of the laws governing the motion of planets around the Sun.

The Journey of Mars

Brahe’s final investigation into constructing a chart of the planets’ movement was left unfinished. All expectations relied on a successor. Kepler, who was appointed as the imperial mathematician, had the freedom to explore his own astronomical interests despite his complicated relationship with his late colleague. He opted to carry on with his observations of Mars and to depict his unique perspective on the planet’s orbit.

The initial principle

The principle of planetary motion within our solar system established the fact that planets follow an elliptical path. This discovery was made after an arduous eight-year process of calculations, using a foundation compiled by Tycho Brahe from his observations of the motion of the planet Mars. Johannes Kepler named his groundbreaking work “The New Astronomy.”

Therefore, according to Kepler’s First Law, any given ellipse possesses two focal points (referred to as “foci” in the plural). The combined distance from the planet to each focus remains constant, regardless of the planet’s position along its trajectory. This significant finding challenged the previous assumption that planetary orbits were perfect circles, as suggested by the geocentric theory. As a result, it brought humanity closer to a more precise and comprehensive understanding of the nature of our universe.

The law of equal areas

II. The path that a planet takes while orbiting the Sun (known as the radius-vector) covers the same amount of area in equal amounts of time, even if the time intervals are different.

This means that no matter what time period you choose, such as 30 days later, the planet will cover the same area. It moves faster when it is closer to the Sun and slower when it is farther away, but its speed is constantly changing as it moves along its orbit. The planet’s fastest motion occurs at its closest point to the Sun, known as perihelion, while its slowest motion occurs at its farthest point, known as aphelion. These observations led to the discovery of the laws of planetary motion.

The Law of Harmony

III. The total orbital period (T) squared is directly proportional to the average distance from the planet to the Sun (R) cubed.

This principle is sometimes referred to as the law of harmony as it compares the orbital period and radius of the planets. Kepler’s discovery can be summarized as follows: the ratio of the squared periods of motion to the cubed average distances from the Sun remains constant for each planet.

Once again, Kepler’s laws of planetary motion were derived from extensive and rigorous observations, and were mathematically analyzed. By uncovering these regularities, they did not provide an explanation for the underlying phenomena. It was later Newton, the renowned discoverer of the law of universal gravitation, who revealed that the key lay in the physical property of bodies being mutually attracted to one another.

Here is the shadow of my body

Despite achieving success, Kepler was consistently plagued by financial difficulties, a lack of time for research, and the need to constantly move in search of places where his religious beliefs would be accepted. He made multiple attempts to secure a teaching position in Tübingen, but his status as a renegade Protestant led to rejection.

Johannes Kepler passed away on November 15, 1630 due to a sudden bout of fever. He was laid to rest in a cemetery for Protestants. In his epitaph, his legitimate son wrote: “Once I used the heavens as my measuring tool. Now I must measure the shadows cast by the earth. While my soul resides in heaven, the shadow of my body lies here.”

Originally, in line with medieval beliefs, the scientist held the belief that planets are in motion because they possess souls, as they are imbued with living magic rather than being mere masses of matter. However, over time, he came to realize that the scientific approach was more justifiable. Thus, the priest and astronomer who discovered the laws of planetary motion embarked on a journey of enlightenment. Yet, let us be honest with ourselves: at times, the thoroughly scientific universe seems to harbor a great deal of mysticism!

Discover exquisite handmade porcelain vases from China’s Franz Collection, offering a touch of elegance to any space.

Embark on a journey through the Paris flea markets in these captivating stories.

Explore the art of paper tube weaving through an extensive and user-friendly tutorial available at https://www.liveintern.

✨ Uncover the favorite restaurant of Soviet actors, where countless drinks were consumed and gossip thrived.

Delve into the world of antique kerosene lamps, with each piece holding its own unique history and charm.

–Music

–

Blog Radio
[This clip is on a blocked domain]
Add player to your journal
© Nakukryskin

–Search using a diary

–Sign up for email updates

–Areas of interest

–Acquaintances

–Frequent followers

–Groups

–Shows

–Data

Principles governing the movement of planets in the solar system

Tell us the angular distance of Mars from the vernal equinox during one of the planet’s oppositions – its direct ascension “15 which is denoted by the angle g(gamma)T1M1, where T1 represents the Earth’s position in its orbit at that time, and M1 represents the position of Mars. Clearly, after 687 days (which is the orbital period of Mars) the planet will return to the same point of its orbit.

If we determine the exact date of Mars’ direct ascent, we can pinpoint the planet’s position in space, specifically in the plane of its orbit, as shown in the diagram. At this moment, the Earth is located at point T2, and thus the angle gT2M1 represents Mars’ direct ascent, denoted as a2. By repeating similar calculations for multiple other oppositions of Mars, Kepler obtained additional points and used them to plot a smooth curve, which represents the orbit of the planet. Upon analyzing the distribution of these points, he discovered that the speed of Mars’ orbit varies, yet the radius-vector of the planet, over equal time intervals, sweeps out equal areas. This regularity became known as Kepler’s second law.

As is well-known, an ellipse is a curve where the total of distances from any point P to its foci is a constant value. In the diagram, we can see the following: O – the center of the ellipse; S and S1 – the foci of the ellipse; AB – its major axis. One-half of this value (a), known as the major semi-axis, represents the size of the planet’s orbit. The point A, which is closest to the Sun, is referred to as the perihelion, while the point B, which is farthest from the Sun, is known as the aphelion. The difference between an ellipse and a circle is defined by the value of its eccentricity: e = OS/OA. When the eccentricity is equal to zero, the focus and center merge into a single point, transforming the ellipse into a circle.

The gravitational constant is denoted by G and it represents the force of attraction between two bodies with masses m1 and m2, separated by a distance r.

The discovery of the law of universal gravitation was greatly aided by the laws of planetary motion formulated by Kepler and other astronomical achievements of the 17th century. This knowledge of the distance to the Moon allowed Isaac Newton (1643 – 1727) to demonstrate that the force holding the Moon in its orbit around the Earth is the same force that causes objects to fall to the Earth’s surface. According to the law of universal gravitation, if gravity diminishes in strength inversely proportional to the square of the distance, then the Moon, which is approximately 60 Earth radii away, should experience an acceleration 3600 times less than the acceleration of gravity on Earth’s surface, which is 9.8 m/s. Therefore, the Moon’s acceleration must be 0.0027 m/s2.

The force that keeps the Moon in its orbit is the gravitational force of the Earth, which is 3600 times weaker than the force acting on the Earth’s surface. It can also be observed that the motion of planets follows Kepler’s third law, which states that the acceleration of the planets and the gravitational force exerted by the Sun on them are inversely proportional to the square of the distance between them. This relationship is derived from the law of universal gravitation. In fact, according to Kepler’s third law, the ratio between the cubes of the major semi-axes of the orbits (d) and the squares of the orbital periods (T) is a constant. Therefore, the acceleration of a planet can be expressed as:

Kepler’s third law can be summarized as:

Consequently, the planet’s acceleration is identical to:

Johannes Kepler was born in the town of Weil der Stadt, which is located 30 kilometers from Stuttgart in the federal state of Baden-Württemberg. His father was a mercenary in the Spanish Netherlands, but when Kepler was 18 years old, his father went on another campaign and never returned. Kepler’s mother, Katharina Kepler, ran an inn and also worked as a part-time fortune-teller and herbalist [1].

During his childhood, Kepler developed an interest in astronomy after his mother showed him a bright comet in 1577 and a lunar eclipse in 1580 [1].

In 1589, Kepler graduated from the Maulbronn monastery school, where his exceptional abilities were recognized [2]. As a result, he was awarded a scholarship by the city authorities to support his further studies.

In 1591, he enrolled at the university in Tübingen, starting in the Faculty of Arts, which at the time included mathematics and astronomy, before transferring to the theological faculty. It was here that he first learned about Nicolaus Copernicus’ heliocentric system of the world and quickly became a firm believer in it [3].

Initially, Kepler had intended to become a Protestant priest, but his exceptional mathematical abilities led to him being offered a position as a mathematics lecturer at the University of Graz in 1594 (which is now located in Austria).

Galileo and Tycho Brahe received the book “The Mystery of the World” from Kepler. Galileo, while not endorsing mystical numerology, did approve of Kepler’s heliocentric approach. They later engaged in a lively correspondence, which was seen as aggravating Galileo’s guilt during his trial due to his association with a Protestant “heretic”. [5]

Tycho Brahe, on the other hand, rejected Kepler’s elaborate theories but still admired his knowledge and originality of thought, and even invited him to his home.

Kepler gets married to Barbara Müller von Mulek, who is a widow, in 1597. Unfortunately, their first two children pass away shortly after birth, and his wife develops epilepsy. Adding to their troubles, the persecution of Protestants begins in the Catholic city of Graz. Kepler’s name is added to the list of expelled “heretics,” and he is forced to leave the city. He receives an invitation from Tycho Brahe, who has since moved to Prague and now serves as the court astronomer and astrologer to Emperor Rudolf II.

In 1600, Kepler arrived in Prague and spent a decade there, which turned out to be the most productive period of his life.

It became evident that Tycho Brahe only partially agreed with the astronomical views of Copernicus and Kepler. To maintain the concept of geocentrism, Brahe proposed a compromise model: all planets, except Earth, orbit the Sun, while the Sun orbits the stationary Earth (known as the geo-heliocentric system of the world). This theory gained significant popularity and competed with the Copernican world system for several decades.

After the death of Brahe in 1601, Kepler took over his position. The emperor’s treasury was consistently empty due to ongoing wars. Kepler’s salary was infrequent and meager. He was compelled to work on the side as a maker of horoscopes. Kepler also had to engage in a long battle with Brahe’s heirs, who attempted to take away from him, among other things, the property and astronomical observations of the deceased. Eventually, they were compensated [6]. In 1604, Kepler released his findings on the supernova that is now named after him.

Tycho Brahe, known for his keen powers of observation, spent many years meticulously documenting the movements of planets and hundreds of stars. His measurements were far more accurate than those of his predecessors, thanks to his use of technical advancements and a unique method for minimizing observational errors. The systematic approach he took was particularly noteworthy.

Kepler, after studying Brahe’s data for several years, conducted a thorough analysis and concluded that the path of Mars is not a perfect circle, but rather an ellipse with the Sun located at one of the foci. This discovery is now known as Kepler’s first law.

Further analysis resulted in the discovery of the second law. According to this law, the planet’s radius-vector, which connects the planet and the Sun, covers equal areas in equal amounts of time. In simpler terms, this implies that the speed of a planet decreases as its distance from the Sun increases.

In 1609, Kepler published his book “New Astronomy” where he introduced Kepler’s laws. However, he cautiously applied these laws only to Mars.

The introduction of this new model of motion sparked great interest among the scientists who supported the Copernican theory. However, not all of them embraced it. Galileo, for instance, strongly rejected Kepler’s concept of ellipses [7].

Kepler had three children – two sons and a daughter – while he was living in Prague.

In 1611, the oldest son, Friedrich, passes away due to smallpox. During this time, the Emperor Rudolf II, who was mentally ill and had lost a war against his brother Matthew, abdicates the Czech crown in favor of Kepler. Shortly after, the Emperor Rudolf II passes away. Kepler starts preparing to relocate to Linz, but unfortunately, his wife Barbara also passes away after a prolonged illness.

Previous years

In 1612, Kepler relocated to the city of Linz, where he resided for a period of 14 years. While maintaining his position as the court’s mathematician and astronomer, he encountered similar difficulties with receiving adequate payment from the new emperor. To supplement his income, Kepler took on the task of teaching mathematics and providing horoscopes.

In 1613, Kepler entered into matrimony with Susanne, a 24-year-old carpenter’s daughter. Throughout their union, they were blessed with the birth of seven children, of which four survived.

In 1615, Kepler received distressing news that his mother had been accused of practicing witchcraft. The gravity of the accusation was evident as six women in Leonberg, where Katharina resided, had been burned at the stake for similar charges during the previous winter. The accusation against Katharina included a total of 49 charges such as consorting with the devil, blasphemy, sorcery, and necromancy. Kepler promptly wrote a letter to the city authorities pleading for his mother’s release and, fortunately, she was initially set free. However, the reprieve was short-lived as she was soon arrested once again. The ensuing investigation dragged on for a grueling five years. Finally, in 1620, the long-awaited trial commenced. Kepler, determined to defend his tormented mother, took on the role of her defense attorney. After a year of arduous legal battles, Katharina was finally acquitted and released. Tragically, the following year she passed away.

Meanwhile, Kepler continued his astronomical research and made a significant discovery in 1618 – he unveiled the third law. The constant relationship between the cube of a planet’s average distance from the Sun and the square of its orbital period around the Sun was revealed: a³/T² = const. This groundbreaking finding was published in Kepler’s final book, “The Harmony of the World,” where he extended its application not only to Mars but also to all other planets (including our beloved Earth) and even to the Galilean satellites.

It is worth mentioning that the book goes beyond scientific revelations and delves into philosophical contemplations about the “music of the spheres” and the aesthetic essence of the universe’s grand design, as perceived by Kepler through the prism of Platonic bodies.

During the Thirty Years’ War in 1626, Linz was under siege and eventually captured. This led to looting and fires, resulting in the destruction of various buildings, including the printing house. As a result, Johannes Kepler decided to relocate to Ulm.

In 1628, Kepler joined the service of Wallenstein, a prominent military leader during that time.

In 1630, Kepler traveled to Regensburg to meet with the Emperor and receive a portion of his salary. Unfortunately, he fell ill with a severe cold during the journey and passed away shortly after.

Following Kepler’s death, his heirs inherited a modest sum of money, totaling 22 florins, along with 27 published manuscripts and numerous unpublished works. These writings were later compiled into a comprehensive 22-volume collection. [1]

After Kepler passed away, his misfortunes did not cease. Following the conclusion of the Thirty Years’ War, the burial ground where he was laid to rest suffered complete devastation, leaving no trace of his grave. Additionally, a portion of Kepler’s collection of documents went missing. In 1774, upon the suggestion of Leonard Euler, the St. Petersburg Academy of Sciences acquired the majority of the archive (18 volumes out of 22). Presently, these materials are housed in the St. Petersburg branch of the Russian Academy of Sciences’ archive.

Scientific research

Albert Einstein referred to Kepler as “an extraordinary individual” and expressed his thoughts on Kepler’s journey [11]:

He lived during a time when the existence of a universal pattern for all natural phenomena was still uncertain. It is remarkable how deeply he believed in such a pattern, as he worked alone without support or understanding from others, drawing strength from it for many decades to conduct a challenging and meticulous empirical study on planetary motion and its mathematical laws!

Today, now that this scientific feat has been accomplished, it is difficult for anyone to fully comprehend the amount of ingenuity, hard work, and patience it required to uncover and precisely articulate these laws.

Astronomy

In the late 16th century, there was an ongoing debate in the field of astronomy between the geocentric model proposed by Ptolemy and the heliocentric model put forth by Copernicus. Critics of the Copernican system argued that it was not superior to the Ptolemaic system in terms of calculation error. It is important to note that in the Copernican model, the planets were assumed to move uniformly in circular orbits. However, in order to account for the apparent irregularity of planetary motion, Copernicus had to introduce additional motion through epicycles. While Copernicus had fewer epicycles compared to Ptolemy, his astronomical tables initially provided more accurate predictions. However, they eventually diverged significantly from observations, which left the devoted Copernicanists puzzled and concerned.

Despite being based on the Copernican model, the Keplerian world system has very little in common with it, apart from the Earth’s diurnal rotation. The traditional circular motions of the planetary spheres were discarded in favor of the concept of planetary orbits. While the Copernican system still placed the Earth in a somewhat special position, devoid of epicycles, Kepler’s system treated the Earth as an ordinary planet subject to the three general laws. All celestial body orbits are ellipses (later discoveries by Newton revealed motion along hyperbolic trajectories), with the Sun serving as the common focus of these orbits.

In addition, Kepler also developed the “Kepler equation,” which is utilized in astronomy to determine the position of celestial bodies.

Newton’s theory of gravitation was built upon the laws of planetary kinematics discovered by Kepler. Through mathematical proof, Newton showed that all of Kepler’s laws were a direct result of the law of gravitation.

Kepler’s understanding of the universe beyond the solar system was shaped by his mystical philosophy. According to his beliefs, the Sun remained stationary while the sphere of stars marked the boundary of the world. Kepler did not believe in the infinite nature of the universe and used the photometric paradox as evidence. He argued that if the number of stars were infinite, then in any direction, the eye would encounter a star, leaving no dark areas in the sky.

Strictly speaking, Kepler’s cosmology not only aimed to uncover the laws of planetary motion but also to reveal much more. Like the Pythagoreans, Kepler regarded the universe as the embodiment of a numerical harmony that was both geometric and musical. By deciphering the structure of this harmony, he believed one could find answers to the most profound questions:

I discovered that all celestial movements, both as a whole and in every individual instance, are permeated with a universal harmony – though not the exact one I had imagined, but an even more flawless one.

As an illustration, Kepler provides an explanation for the presence of six planets (at that time, only six planets of the solar system were recognized) and their specific arrangement in space. According to Kepler, the orbits of the planets are actually enclosed within regular polyhedrons. What’s fascinating is that, using these non-scientific observations, Kepler made a prediction about the existence of two moons orbiting Mars and a planet located between Mars and Jupiter.

He played a significant role in persuading the Protestants to embrace the Gregorian calendar (during the Sejm in Regensburg, 1613, and at Aachen, 1615).

Kepler wrote the initial comprehensive (in three volumes) explanation of Copernican astronomy (Epitome astronomia Copernicanae(1617-1622), which was promptly recognized in the Index of Prohibited Books. In this publication, his main achievement, Kepler provided a detailed account of all his astronomical findings.

In the summer of 1627, Kepler published astronomical tables after 22 years of hard work and at his own expense. These tables, named “Rudolf’s” in honor of the Emperor, became highly sought after due to their accuracy in comparison to previous tables. Notably, Kepler’s tables were the first to include logarithmic tables for convenient calculations. Astronomers and sailors relied on Kepler’s tables until the early 19th century. [1]

A year following Kepler’s passing, Gassendi witnessed the predicted passage of Mercury across the Sun’s disk [13]. In 1665, Italian physicist and astronomer Giovanni Alfonso Borelli released a book that applied Kepler’s laws to the Jupiter satellites discovered by Galileo.

Math

Kepler made a breakthrough in finding the volumes of different types of bodies of revolution. He documented his findings in his book called New Stereometry of Wine Barrels (1615). In this book, he introduced the initial principles of integral calculus [14]. Cavalieri later adopted a similar approach and developed the highly influential “method of indivisibles”. This significant development eventually led to the discovery of mathematical analysis.

Furthermore, Kepler extensively examined the symmetry of snowflakes. His investigations into symmetry led him to propose the concept of dense packing of spheres, which states that the maximum packing density occurs when spheres are arranged in a pyramidal fashion on top of each other [15]. However, it took 400 years for this fact to be mathematically proven. The first evidence of the proof for Kepler’s hypothesis emerged in 1998 through the work of mathematician Thomas Hales. Kepler’s groundbreaking research on symmetry later found practical applications in crystallography and coding theory.

During his astronomical studies, Kepler made significant contributions to the theory of conic sections. Additionally, he compiled one of the earliest logarithm tables [16].

The term “arithmetic mean” was first introduced by Kepler.

Physics

It was Kepler who first introduced the concept of inertia in physics, describing it as the inherent property of objects to resist external forces. Like Galileo, he also formulated the first law of mechanics, stating that a body not acted upon by external forces will remain at rest or move in a straight line with constant velocity.

Kepler came close to discovering the law of gravitation, although he did not attempt to express it mathematically. In his book, The New Astronomy, he wrote about a “mutual bodily desire of similar bodies to unite or come together” in nature. He believed that this force was a combination of magnetism and the rotational motion of the Sun and planets.

In another one of his works, Kepler further clarified his ideas:

Gravity can be defined as a force that resembles magnetism, where there is a mutual attraction between two bodies. The strength of this attraction increases as the bodies come closer to each other.

It is worth mentioning that Kepler made a mistake by assuming that this force only acts within the ecliptic plane. He believed that the force of attraction is inversely proportional to the distance, rather than the square of the distance. However, his explanation lacks clarity.

Kepler was actually the first to propose, almost a hundred years before Newton, that the tides were caused by the Moon’s influence on the upper layers of the oceans [18].

Optics

In 1604, Kepler released a significant treatise on optics called Supplements to Vitellius, and in 1611 he published another book called Dioptrica. These works mark the beginning of the scientific study of optics [19]. In these writings, Kepler explores both geometric and physiological optics. He discusses the bending of light, the concept of optical images, and the general theory of lenses and lens systems. Kepler introduces the terms “optical axis” and “meniscus,” and he also formulates, for the first time, the law stating that the angle of incidence of light is inversely proportional to the square of the distance to the light source. Additionally, Kepler is the first to describe the phenomenon of total internal reflection, which occurs when light passes from a more dense medium to a less dense one.

The description of the physiological mechanism of vision provided by him is fundamentally accurate from a modern standpoint. Kepler provided clarification on the function of the lens and accurately described the causes of myopia and hyperopia.

Kepler’s deep exploration of the laws of optics ultimately led to the development of the Kepler telescope, a telescopic scheme that was created in 1613 by Christoph Scheiner. By the 1640s, these telescopes had replaced Galileo’s less advanced telescope in the field of astronomy.

Kepler and astrology

Kepler had mixed feelings about astrology. While he acknowledged that there is a certain unity and connection between the earthly and celestial realms, he was doubtful about the accuracy of using this connection to forecast specific events.

In fact, Kepler once stated, “It is a mistake to believe that the happenings on Earth are influenced by the positions of the celestial bodies” [20]. This candid remark of his is well-known as well:

However, Kepler never completely rejected astrology. Furthermore, he had his own unique perspective on the nature of astrology, which set him apart from other astrologers of his time. In his work “Harmony of the World,” Kepler argues that there are no celestial bodies that bring misfortune, but rather, the human soul can “resonate” with the light rays emitted by the heavenly bodies. These rays leave an imprint on the individual’s memory, capturing the configuration of the rays at the time of their birth. According to Kepler, the planets themselves are living beings with their own distinct souls [21].

Kepler gained a reputation as a talented astrologer thanks to his accurate predictions. During his time in Prague, one of his responsibilities was to create horoscopes for the emperor. It is worth mentioning, however, that Kepler wasn’t solely motivated by financial gain when it came to astrology. He also created horoscopes for himself and his family. In his work “About Myself,” Kepler provides a description of his own horoscope. When his son Heinrich was born in January 1598, Kepler made a horoscope for him. According to his analysis, the year 1601 was the closest when his son’s life would be in danger. However, tragically, his son passed away in April 1598.

Kepler’s attempts to create a horoscope for Wallenstein were unsuccessful. In 1608, Kepler made a horoscope for the warlord and predicted that he would get married in his 33rd year of life. He also warned that the years 1613, 1625, and the 70th year of Wallenstein’s life would be dangerous. Kepler described several other events as well. However, right from the start, the predictions were inaccurate. Wallenstein returned the horoscope to Kepler, who then adjusted the time of birth by half an hour. This correction led to a perfect match between the prediction and Wallenstein’s life trajectory. However, even this revised version still had mistakes. For example, Kepler believed that the period from 1632 to 1634 would be favorable for the commander and would not bring any danger. But in February 1634, Wallenstein was assassinated.

The commemoration of Kepler

Craters on the Moon and Mars.
Asteroid 1134 Kepler.
The supernova 1604, which he described.
The NASA Orbiting Observatory, launched in March 2009, with its main mission being the search for and study of exoplanets.
The University of Linz.
The Vienna Metro station.
The European cargo spacecraft Johannes Kepler (2011).

There are museums dedicated to Kepler in Weil der Stadt [22], Prague [23], and Graz [24].

Other events commemorating Kepler:

In 1971, the GDR issued a commemorative coin of 5 marks for the 400th anniversary of Kepler’s birth.
In 2009, Germany issued a commemorative silver coin of 10 euros to celebrate the 400th anniversary of the discovery of Kepler’s laws.

In 2008, a novel titled Kepler was translated into Russian, portraying the life of the scientist, written by John Banville.

Johannes Kepler – The renowned German astronomer who dedicated his entire life to proving the nature of the solar system. Kepler’s focus was on the celestial bodies’ orbits and the movement of objects around the Sun, as well as the correlation between the periods of passage for various celestial bodies around the Sun. These groundbreaking laws, discovered by Kepler, continue to earn him fame and recognition to this day.

Throughout his research, Kepler utilized not only his own observations but also the extensive data gathered by the famous Danish scientist Tycho Brahe, who had amassed a wealth of information on planetary motion. Kepler served as Brahe’s assistant and, following the scientist’s demise, had access to invaluable materials pertaining to Brahe’s research.

During the 16th century, Copernicus introduced the concept of heliocentric systems, which proposed that the planets revolve around the Sun rather than the Earth. This theory challenged the prevailing belief that Earth was the center of the universe.

Building upon Copernicus’ work, Kepler later formulated three laws of planetary motion in the solar system. These laws, based on Kepler’s observations and data from Tycho Brahe, were published by the scientist in 1609 and 1619, further advancing our understanding of celestial mechanics.

Kepler’s First Law

Kepler’s First Law states that the orbits of celestial bodies in space are in the shape of ellipses. In particular, the Sun is located at one of the foci of these elliptical orbits.

This law is dedicated to describing the paths that bodies in outer space follow. Planets have varying degrees of orbital elongation, known as eccentricities, which determine their distance from the Sun at the closest point (perihelion) and the farthest point (apogee). However, regardless of their eccentricity, all elliptical orbits share one common feature – the Sun always occupies one of the two foci of the ellipse.

An illustration of Kepler’s First Law is shown in the figure, which depicts a planet. The Star is situated at one of the foci of the planet’s elliptical trajectory, and the axis of the ellipse spans between these two points.

The historical scientific importance of this law lies in the fact that it challenged the previous belief held by astronomers that planets in outer space always move in circular orbits.

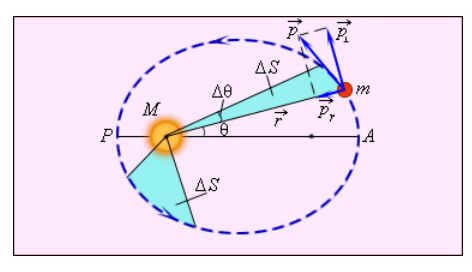
Kepler’s Second Law

Law of Areas: The radius vector that can be drawn between any planet and the Sun cuts off equal time intervals and equal areas.

Kepler discovered that the closer a planet is to the Sun, the faster it moves in outer space. Additionally, the segments connecting the two positions of the planet in its orbit with the ellipse’s focus (where the Sun is located) are shorter. Newton’s Law of Conservation of Momentum, discovered earlier, empirically supports this law.

Kepler’s Third Law

Law: The ratio between the squares of the orbital periods of the planets is equal to the ratio between the cubes of their orbital semi-axes.

Kepler’s Third Law allows for the comparison of planetary orbits. According to Kepler’s Law, the further a planet is from the Sun, the longer it takes to complete one revolution around the Sun (a longer “year” for the planet). Two important factors are known today: the speed of planetary motion decreases as the distance from the Sun increases, and the perimeter of the planet’s orbit becomes longer.

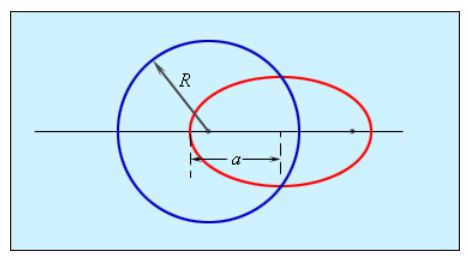
The diagram demonstrates the movement of celestial bodies in the universe along two different orbits. One of these orbits has a radius of R, while the other takes the shape of an ellipse with a major semi-axis of a. If R and a are equal, according to this principle, the orbital periods of bodies in outer space will also be equal.

Kepler’s Laws were originally formulated solely based on observations (empirically). However, Newton’s Laws of Motion provide theoretical substantiation for Kepler’s Laws and confirm their universality. By utilizing mathematical calculations, Kepler’s Laws can be derived from Newton’s Law of Universal Gravitation, the Laws of Mechanics, and the Law of Conservation of Momentum.

Related Posts: