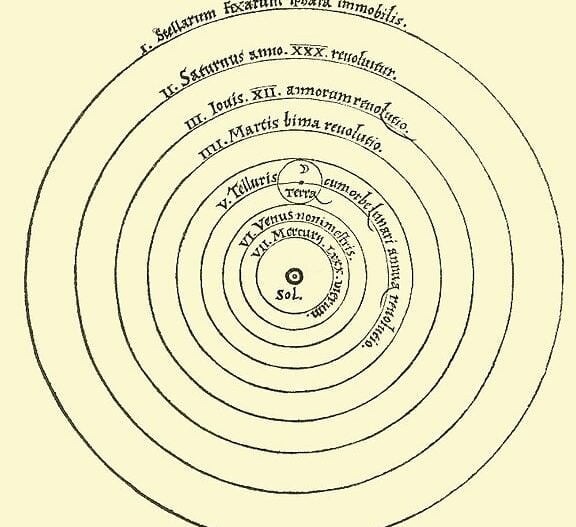
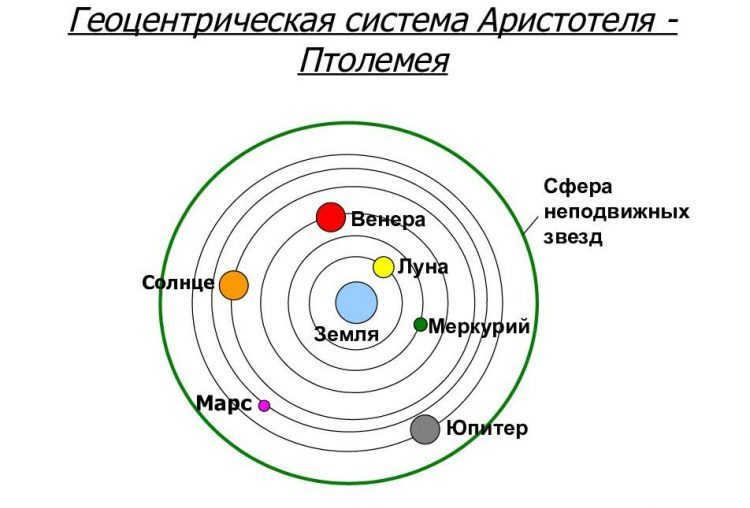
In the late 16th century, there was a significant debate in astronomy between two models of our solar system: the geocentric model, originally proposed by Ptolemy, which stated that the Earth was the center of rotation for all celestial bodies, and the heliocentric model, introduced by Copernicus, which proposed that the Sun was the central body.
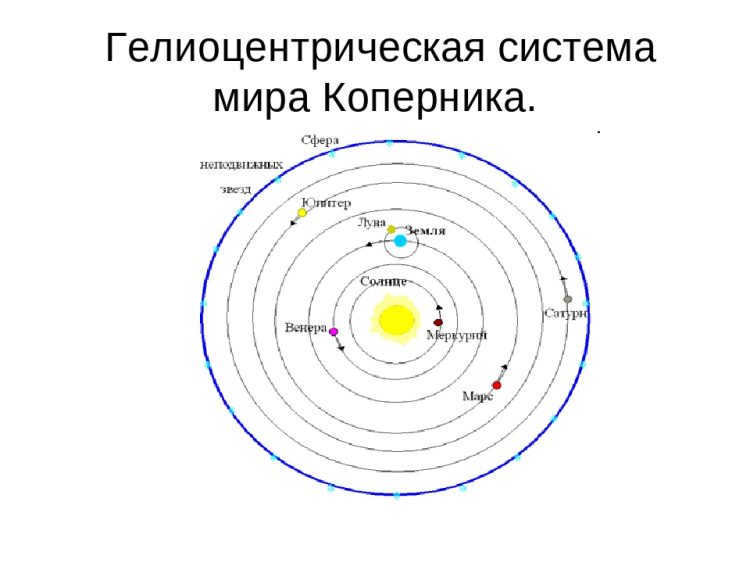
Despite being closer to the true understanding of the solar system, Copernicus’ work had certain imperfections. The main flaw was the claim that the planets orbit the Sun in circular paths. This assertion made Copernicus’ model nearly as inconsistent with observations as Ptolemy’s system. To address this inconsistency, the Polish astronomer proposed an additional movement of the planets in circular paths, with the center of these paths already moving around the Sun – known as an epicycle. However, this adjustment did not completely resolve the discrepancies in the model.
During the early 17th century, the renowned German astronomer Johannes Kepler thoroughly examined the planetary system proposed by Nicolaus Copernicus. Additionally, he carefully analyzed the astronomical observations conducted by the Danish scientist Tycho Brahe. Based on this comprehensive research, Kepler formulated the fundamental principles governing the motion of planets, which became widely known as Kepler’s Three Laws.
Tycho Brahe, an exceptional observer, dedicated many years to compiling an extensive record of planetary observations and countless stars. The precision of Brahe’s measurements surpassed that of all his predecessors.
Kepler’s law of orbital ellipses.
The celestial bodies within the solar system follow a path of elliptical orbits, with one of the foci being occupied by the Sun.
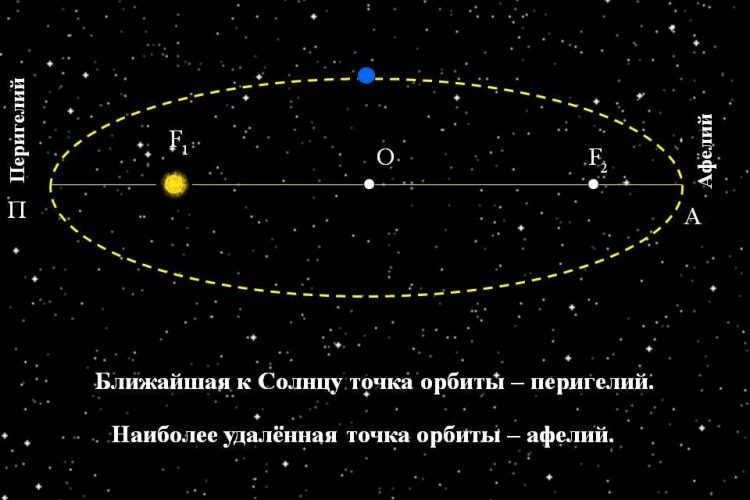
As per Kepler’s initial principle, each of the planets within our system follow a closed curve known as an ellipse. Our star is positioned at one of the foci of the ellipse. There are two foci: these are two points inside the curve, where the sum of the distances to any point on the ellipse remains constant.
After extensive observations, scientists have discovered that the orbits of all the planets in our system are nearly in the same plane. Some celestial bodies travel along elliptical orbits that resemble circles. Only Pluto and Mars travel in more elongated orbits. Hence, Kepler’s first principle is referred to as the principle of ellipses.
A planet’s radius-vector traces out equal areas in equal time intervals.
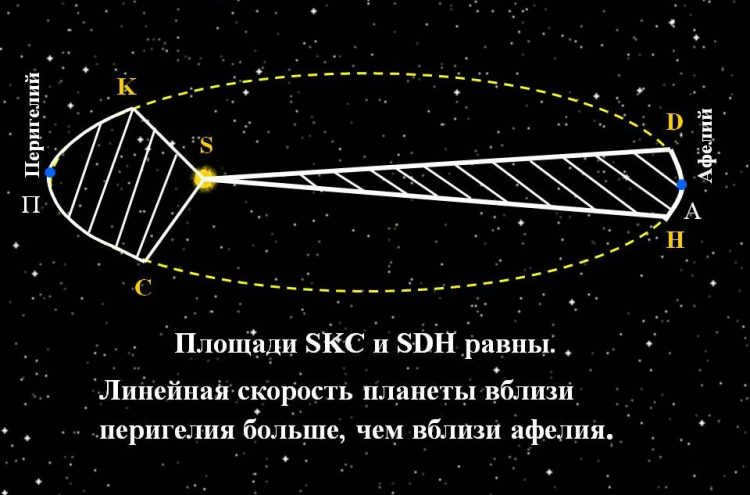
The second principle established by Kepler states that each planet’s movement occurs within a plane that intersects with the center of our star. Additionally, the radius vector linking the Sun and the specific planet traces out equal areas. Consequently, it becomes evident that the celestial bodies orbit the yellow dwarf in an uneven manner, reaching their maximum velocity at perihelion and minimum velocity at aphelion.
This phenomenon can be observed in the Earth’s motion. Every year, in early January, our planet accelerates as it passes through perihelion. As a result, the Sun moves more swiftly along the ecliptic than during other times of the year. Conversely, in early July, the Earth reaches aphelion, causing the Sun to move at a slower pace along the ecliptic.
Harmonic Law: Kepler’s Third Law
The relationship between the squares of the orbital periods of the planets and the cubes of the major semi-axes of their orbits.
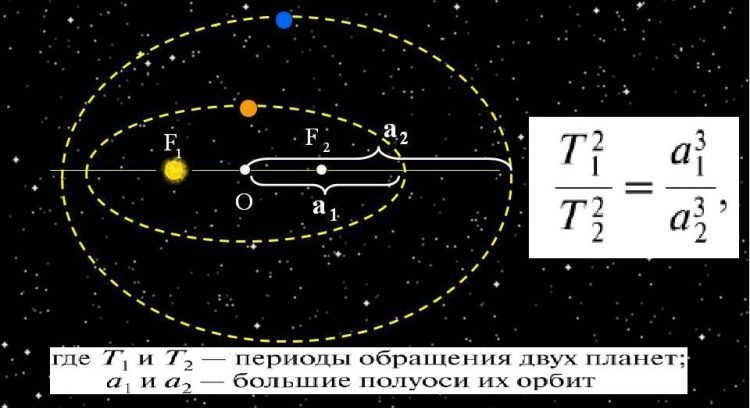
Kepler’s third law establishes a relationship between the orbital period and average distance of planets or satellites from a luminary. This law holds true for both planets and satellites, with an accuracy of less than 1%.
By applying this law, it is possible to calculate the duration of a planet’s year (the time it takes to complete one revolution around the Sun) if its distance from the Sun is known. Conversely, the same law can be used to determine the orbit when the period of revolution is known.
Despite the fact that Kepler’s laws had a relatively small margin of error, they were acquired through observation and experimentation, lacking any theoretical backing. Fortunately, this issue was resolved by none other than Isaac Newton, who, in 1682, unveiled the groundbreaking law of universal gravitation.
Undoubtedly, Kepler’s laws played a pivotal role in comprehending and outlining the movement of celestial bodies.
Video
Reword the text, making it unique, using the English language and preserving the HTML markup:
Video
Final examination in the field of astronomy
Final examination “Elements of Astronomy”
Astronomy is a scientific discipline that investigates ….
A) the movement and origin of celestial bodies and their systems.
B) the formation of celestial bodies and their characteristics.
C) the movement, characteristics, origin, and development of celestial bodies and their systems.
Astronomy requires the use of a telescope to ….
A) collect light and generate an image of the source.
B) gather light from a celestial object and expand the field of view at which the object is observed.
C) acquire an enlarged image of a celestial body.
The highest point of the celestial sphere is known as …
A) the northern point. B) the zenith. C) nadir. D) the eastern point.
The term used to describe the angle at which a star sees the radius of the Earth’s orbit is A) parallax.
A) parallax. B) stellar magnitude. C) astronomical unit.
The planet that is third in order from the Sun is ….
A) Saturn. B) Venus. C) Earth.
What type of orbits do the planets have around the Sun?
A) circles. B) ellipses that are close to circles. C) the branches of parabolas.
The point in a planet’s orbit that is closest to the Sun is called …
A) perihelion. B) aphelion. C) eccentricity.
The coldest surface temperatures can be found on …
A) yellow stars. B) orange giants C) white dwarfs.
All giant planets share the characteristic of ….
A) fast rotation. B) slow rotation.
Asteroids orbit between the paths of …
A) Venus and Earth. B) Mars and Jupiter. C) Neptune and Pluto.
What are the predominant substances in the atmospheres of stars?
A) helium and oxygen. B) nitrogen and helium. C) hydrogen and helium.
To which class of stars does the Sun belong?
A) supergiant. B) a yellow dwarf. C) white dwarf. D) red giant.
How many constellations is the sky divided into?
A) 108. B) 68. C) 88.
Who discovered the laws of planetary motion around the sun?
A) Ptolemy. B) Copernicus. C) Kepler. D) Bruno.
Which layer of the Sun is the main source of visible radiation?
A) Chromosphere. B) Photosphere. C) The solar corona.
Stars that emit periodic pulses of radio waves are called ….
A) quasars. B) pulsars. C) black holes.
CONTROL WORK #4 “Elements of Astronomy”.
What is the field of cosmology?
A) a discipline that investigates the movement and origin of celestial bodies and their systems.
B) a field of study that examines the structure and evolution of the universe.
C) the scientific field that explores the laws governing the motion of celestial objects.
Parsec serves as a unit of measurement for ….
A) the brightness of celestial bodies. B) the dimensions of celestial bodies.
C) the distances between celestial bodies.
The nadir refers to ….
A) the northern point. B) the zenith. C) the lowest point on the celestial sphere. D) the eastern point.
The equivalent of longitude in geographical coordinates is .
A) the meridian. B) the true horizon. C) the right ascension.
Entering the Earth’s atmosphere and traversing it, small solid particles are known as a .
A) meteor. B) comet. C) meteorite.
The planet that is sixth in order from the Sun is ….
A) Saturn. B) Jupiter. C) Uranus.
The apparent movement of the planets in the sky is ….
A) circular motion. B) a loop-shaped motion. C) straight-line motion.
The point in a planet’s orbit that is farthest from the Sun is called ….
A) perihelion. B) aphelion. C) eccentricity.
Which type of stars have the highest surface temperatures?
A) blue dwarfs. B) yellow stars. C) red giants.
Consisting of elements that are heavy in weight are ….
A) giant planets. B) terrestrial planets.
The duration of solar activity is …
A) 10 years. B) 12 years. C) 11 years.
What is the appearance of the Milky Way galaxy?
A) elliptical. B) spiral. C) irregular.
Belonging to what category of stars is Betelgeuse?
A) a supergiant. B) a yellow dwarf. C) a white dwarf. D) an orange giant.
What is the total number of stars that can be observed in the sky in a single day?
A) Approximately 2500 stars. B) Approximately 5000 stars. C) Approximately 10000 stars.
Who is credited as the founder of the heliocentric model of the universe?
A) Ptolemy. B) Copernicus. C) Kepler. D) Bruno.
What is the name of the outermost layer of the solar atmosphere?
A) Chromosphere. B) Photosphere. C) The solar corona.
Celestial objects that emit powerful radio waves are known as ….
A) quasars. B) pulsars. C) black holes.
Recommended criteria for evaluating work:
7 – 10 correct answers – "3",
11 – 14 correct answers – "4",
15 – 17 correct answers – "5".
“Management of a general education organization:
New Trends and Modern Technologies”
Certificate and discount on training for each participant
We are currently seeking educators to join the Infowork team
Material number: 78193042116
These courses will pique your interest:
Post a comment
Get authorized to post your inquiries.
Advice from educators on preparing for the Unified State Exam: the key to success
The cost of first-year tuition at Russian universities has risen by 10% in the past year
Every year, at least 500 thousand children in Russia will be taught how to swim
Review of the beloved fairy tale “Evenings at the Farmstead near Dikanka”
Rospotrebnadzor reports a high prevalence of COVID-19 among children
The regional round of the All-Russian Olympiad for schoolchildren has begun
Online conference on managing educational institutions
Gift vouchers
The users who have posted the materials on the site are responsible for resolving any conflicts regarding the materials and their content. Nevertheless, the site administration is willing to offer assistance in addressing any concerns related to the site’s operation and content. If you come across any unauthorized use of materials on this site, kindly notify the site administration via the provided feedback form.
All content published on this website is either created by the website’s authors or contributed by its users, and is provided for informational purposes only. The copyrights for these materials belong to their respective authors. Any unauthorized reproduction, in whole or in part, of the website’s content is strictly prohibited without the written permission of the website’s administration. Please note that the views expressed by the administration may not necessarily reflect those of the authors.
We have already calculated the linear and angular velocity of Earth’s rotation around its own axis. Today, let’s examine the Earth’s motion around the Sun and determine its speed. Additionally, we will discuss Kepler’s three laws, as they are essential to understanding this topic.
Method 1
What is the speed at which the Earth revolves around the Sun? The initial approach is to utilize the familiar equation for finding linear velocity:
The distance from Earth to the Sun is known as one astronomical unit or 149,597,870,700 meters. The period of revolution is equal to one year. When converted to seconds, it amounts to 31,536,000 s.
By substituting these values into our equation and performing the calculation, we can find the answer.
Another approach
However, there is an alternative method we can pursue. The initial speed of the Earth can be determined by considering the Sun’s gravitational pull, which corresponds to the first cosmic velocity. It is worth recalling the formula used to calculate the first cosmic velocity:
Where G represents the gravitational constant, R denotes the distance between the Earth and the Sun, and M represents the mass of the Sun. By accurately measuring the mass of the Sun and plugging it into the equation, we can calculate the initial speed:
Typically, for convenience, the speed is approximated and expressed as 30 km/s or 108,000 km/h. Interestingly, the latter figure holds particular significance in Hinduism, as the number 108 is considered sacred. In fact, Hindus have even defined the value of Pi as the ratio 339/108. However, let us now return to the concept of velocity.
Kepler’s first law.
In our calculations, we assume that the Earth moves uniformly in a circular path. However, in reality, this is not entirely accurate.
Johannes Kepler (1571 – 1630).
During the early 17th century, the German astronomer Johannes Kepler examined years of observations on the planet Mars, which were obtained from his teacher, the Danish astronomer Tycho Brahe. From these observations, he deduced that all the planets in the solar system do not move in perfect circles, but rather in ellipses, with the Sun located at one of the foci. This principle is known as Kepler’s first law.
All the planets in the solar system orbit in an elliptical path, with the Sun positioned at one of the focal points.
Now, let’s delve into the concept of an ellipse and its foci.
What is an ellipse?
An ellipse is a geometric shape defined as the set of all points on a plane. These points have the property that the sum of the distances from each point to two fixed points on the plane, known as the foci, is a constant value greater than the distance between the foci.
To better understand this concept, let’s consider a simple example. Imagine we have a piece of string with stationary buttons attached to each end. We stick the buttons into a piece of plasterboard, which we found in the garage after completing some repairs.
Next, we take a pencil and draw lines by pressing it against the string. The resulting shape is an ellipse, and the points where we attached the buttons are referred to as the foci.
Primary and secondary semi-major axis
Crucial characteristics of the ellipse include its primary semi-major axis. It is commonly represented by the Latin letter “a”, and secondary, which is represented by the letter “b”. Also Latin.
The primary semi-major axis – is the measurement from the center of the ellipse to its furthest point. Similarly, the secondary semi-major axis – is the measurement from the center to the nearest point of the ellipse.
Eccentricity
Another important characteristic of an ellipse is its eccentricity, which is represented by the letter “e” and is defined as the ratio of the focal length of the ellipse (c) to the major semi-axis (a).
An ellipse is sometimes referred to as a flattened circle, and the eccentricity indicates how much the circle is flattened.
The closer the eccentricity is to one, the more elongated the ellipse becomes. On the other hand, an eccentricity close to 0 means that the ellipse is very similar to a circle. In fact, we can say that a circle is an ellipse with an eccentricity of 0.
In the solar system, Venus has the smallest eccentricity of only 0.007, making its trajectory almost circular. Comets, on the other hand, have eccentricities close to one. For example, the comet Galea has an eccentricity of 0.967.
Aphelion and Perihelion
The point at which a planet is closest to the Sun is known as perihelion. It is derived from the Greek words “peri” meaning near and “helios” meaning Sun. The opposite point to perihelion is called aphelion. This is the point where the planet is farthest away from the Sun.
The Earth reaches perihelion in early January, when it is approximately 147.1 million kilometers away from the Sun. It reaches aphelion in early July, when it moves approximately 152.1 million kilometers away. The difference between the two points is approximately 5 million kilometers.
This phenomenon can partially explain why winters in the northern hemisphere tend to be milder than in the southern hemisphere. In winter, the Earth is slightly closer to the Sun. Conversely, since the Earth receives less solar energy in July, summers in the northern hemisphere are cooler.
Kepler’s Second Law
As we have previously mentioned, Kepler’s first law states that the Earth orbits the Sun in an elliptical path rather than a perfect circle. Additionally, the Earth’s velocity varies depending on its distance from the Sun. It speeds up as it gets closer and slows down as it moves further away.
Kepler’s second law can be summarized as:
When a planet is at equal time intervals, the area it sweeps out is equal.
This law is also known as the law of areas. While this formulation may seem unimportant, it is actually closely related to the law of conservation of momentum. However, what interests us more is the following equation:
The multiplication of the linear velocity and the radius vector at the perihelion is equal to the multiplication of the velocity and the radius vector at the aphelion. This situation represents a specific instance of Kepler’s second law, specifically for the maximum and minimum values of the velocity of the planet.
Maximum and minimum velocity of the Earth’s movement
By knowing this, it becomes possible to calculate the speeds at which the Earth moves at the perihelion and aphelion. In other words, determine its maximum and minimum velocities. However, the law of conservation of energy is required here.
Additionally, there are formulas available for determining the distance from the sun to the aphelion and perihelion, using the eccentricity and major semiaxis:
Furthermore, there is an equation for finding the initial spatial velocity.
We substitute the single distance R in the equation with a, which represents the semi-major axis. The semi-major axis of the Earth’s orbit is the average distance between the Earth and the Sun, and it is this value that we initially used in our calculations. Therefore, the velocity we obtained at the beginning is the average orbital velocity. This is the velocity we will be using.
We establish a set of equations and from a physics standpoint, the problem is solved. The only thing left is the math.
To solve the problem, we begin by reducing the mass of the Earth in the law of conservation of energy, and we also replace the radius vectors with their respective values, , .
If we carefully examine the situation, we can observe that the square of the average orbital velocity is present in the relationships , and . We have already computed this value earlier, so it would be convenient to substitute it here.
Next, we can solve for in the first equation and substitute it into the second equation. By making the necessary transformations, we can express :
Finally, we can also solve for :
All that’s left is to substitute the given values and perform the calculations.
Kepler’s Third Law
In 1609, Johannes Kepler published his two laws, but he didn’t stop there. He continued his search and, ten years later, made a breakthrough with the discovery of the third law.
The relationship between the squares of the stellar periods of the planets’ orbits is equal to the cubes of the major semi-axes of those orbits.
By the late 16th century, followers of Copernicus, particularly Johannes Kepler, recognized the need for further development and refinement of his theory in order for it to gain wider acceptance.

The renowned German scientist, Johannes Kepler (1571-1630), made significant contributions to the fields of mathematics, mechanics, astronomy, and optics. He is best known for his groundbreaking discovery of the laws governing the motion of planets within the solar system.
The Hypothesis of Non-Uniform Planetary Motion
In his quest to determine the true paths followed by planets as they orbit the Sun, Kepler analyzed extensive astronomical observations collected by Tycho Brahe over many years. These measurements, which boasted an unprecedented level of accuracy for the pre-telescopic era, allowed Kepler to challenge the prevailing assumption of uniform planetary motion. Instead, he proposed that the speed at which planets travel along their orbits varies, with faster speeds occurring when they are closer to the Sun and slower speeds when they are farther away.
Simultaneously, the planet’s orbits continued to revolve around him in circular paths, albeit with the Sun positioned off-center. It became imperative to mathematically express the relationship between a planet’s distance from the Sun and the time it took to complete specific segments of its journey.
By this point, algebra, geometry, and trigonometry, which represented the mathematics of fixed values, had amassed a considerable amount of data, enough to form a comprehensive body of knowledge, despite the presence of numerous unresolved and unfinished aspects.
Kepler’s Laws
However, Kepler faced a problem that could not be solved using traditional mathematical methods. The problem involved calculating the area of a sector of an eccentric circle, which is equivalent to calculating an elliptic integral in mathematical analysis.
Although Kepler was unable to find a solution using quadrature, he did not give up in the face of difficulties. Instead, he approached the problem by summing an infinite number of “actualized” infinitesimals. This atomistic approach to solving a complex astronomical problem was a groundbreaking step in the development of mathematical analysis during that time period, and its significance cannot be overstated.
Kepler introduced a new concept in mathematics by considering a certain integral as the area of a curvilinear trapezoid bounded by a curve (conchoid). This marked a significant advancement in the field of variable mathematics. The calculation methods he used here align closely with modern approaches to approximate integration.
By solving this problem for the case of an eccentric circle, Kepler made a groundbreaking discovery in the early 17th century (in 1602) – the second law of planetary motion. (“The areas described by the radius-vectors ‘planet – Sun’ at equal intervals of time are equal to each other”).
Therefore, the groundbreaking law of the revolutionary celestial mechanics is uncovered using a specially developed, groundbreaking mathematical method, marking the dawn of a new era in mathematics – the era of variable mathematics.
Three years later, in 1605, after an incredibly arduous calculation process involving the validation of various hypotheses, Kepler successfully unveils the initial law. (“The planets orbit in elliptical paths with the Sun situated at one of the focal points”.) The mathematical perspective on determining the sectorial area set by Kepler for this scenario remains largely unchanged.
New mathematical techniques
In 1615, he released his publication titled “Innovative Stereometry of Wine Casks”, where he continued to advance integration techniques and applied them to determine the volumes of over ninety complex rotational bodies. He also explored challenging problems, leading to the emergence of a new branch of infinitesimal calculus known as differential calculus.
Kepler’s groundbreaking work did not go unnoticed, and in 1616, A. Anderson and later I. Guldin criticized his methods for summing infinitesimals without realizing that despite their apparent rigidity, these methods were highly productive and contained crucial ideas for the future advancement of mathematics.
On the contrary, at that time, B. Cavalieri, a student of Galileo, highly praised Kepler’s work and made significant contributions to the development of the ideas contained in them. Consequently, the methods and findings of Kepler and Cavalieri captured the attention of numerous prominent mathematicians of the 17th century, sparking a surge of research in the emerging field of mathematics, particularly in the last quarter of the century. This research focused on differential and integral calculus.
As a result, variable mathematics dominated the realm of mathematical knowledge for an extended period and became the most potent tool for investigating increasingly complex problems in natural science and technology.
The desire to enhance astronomical computations captivated Kepler, leading him to delve into the theory and application of logarithms. In parallel with Neeper (and Bürgi), Kepler developed his own version of logarithmic theory (in contrast to Neper – who relied solely on arithmetic) and utilized it to construct logarithmic tables that closely resembled Neper’s, yet boasted greater precision. These tables were initially published in 1624 and remained in circulation until 1700.
However, Kepler’s most significant contribution was his pioneering use of logarithmic calculations in the creation of the renowned Rudolphine planetary tables. These tables were based on the Copernican model of the solar system and Kepler’s laws of planetary motion, and served as an invaluable reference for astronomers worldwide for an extended period of time.
The emergence of Copernican astronomy also acted as a catalyst for the advancement of automated calculation. Wilhelm Schickard, a close associate of Kepler and an advocate for the Copernican theory, constructed the first-ever calculating machine capable of performing all four basic arithmetic operations around 1623. Two other notable figures in this field were the renowned mathematicians Pascal (1642) and Leibniz (1674). However, the technological capabilities of that era were still insufficient to consider mass-producing dependable computing devices.
Kepler’s fascination with second-order curves, on one hand, and the challenges of astronomical optics, on the other (both stemming from the needs of advancing Copernican astronomy), guided him towards formulating the overarching principle of continuity. The general principle of continuity serves as a crucial heuristic method enabling the derivation of an object’s properties from those of another, provided that the former can be attained through a limit transition from the latter.
In his work “Additions to Vitellinus or the optical part of astronomy” (1604), Kepler delves into the study of conic sections, interpreting the parabola as a hyperbola or ellipse with an infinitely distant focus. This marks the earliest application of the general principle of continuity in the annals of mathematics.
Therefore, with the aid of innovative mathematical techniques, Kepler’s discoveries about the motion of celestial bodies provided compelling evidence for the Copernican theory. These findings proved instrumental in enabling Newton to formulate the law of universal gravitation, which ultimately provided a dynamic justification for Copernicus’ theory. Both Kepler and Newton were renowned mathematicians of their era.
(Source: White Y.A. Copernicus, Copernicanism and the Development of Natural Science // Historical and Astronomical Studies. Issue XII. – M.: Nauka, 1975. P. 66-69).
Materials on the Same Topic
In the late 16th century, the field of astronomy was divided between two competing theories: the geocentric system proposed by Ptolemy and the heliocentric system proposed by Copernicus. The supporters of the geocentric system argued that the Copernican model was not superior to the Ptolemaic model in terms of calculating errors. It is important to note that in the Copernican model, the planets were assumed to move uniformly in circular orbits. However, in order to explain the apparent irregularity of planetary motion, Copernicus had to introduce additional motion through the use of epicycles. Although Copernicus used fewer epicycles compared to Ptolemy, his astronomical tables, which were initially more accurate, eventually deviated significantly from observations. This discrepancy puzzled and disappointed the enthusiastic supporters of the Copernican system.
Kepler’s remarkable discoveries of the three laws of planetary motion provided a thorough and precise explanation for the seeming irregularities in the motions of celestial bodies. In place of the complex and artificial system of epicycles, Kepler’s model simplifies things by introducing just one curve, namely the ellipse. The second law elucidates the variations in a planet’s velocity as it moves closer to or farther away from the Sun, while the third law enables us to determine both the velocity and the period of revolution around the Sun.
While the Copernican model served as the basis for the Keplerian world system historically, they actually differ in many ways (except for the Earth’s daily rotation). The old concept of circular motions of planetary spheres carrying the planets was abandoned, and a new idea of planetary orbits emerged. In the Copernican system, the Earth still held a somewhat special position as Copernicus declared it the center of the Earth’s orbit. However, in Kepler’s system, the Earth is treated as a regular planet subject to the three general laws of motion. All celestial bodies move along elliptical orbits (later, Newton discovered motion along hyperbolic trajectories), with the Sun serving as the common focus of these orbits.
In addition, Kepler also derived the “Kepler equation”, which is widely used in astronomy to determine the position of celestial bodies.
The principles of planetary motion that Kepler discovered later formed the foundation for Newton’s theory of gravity. Newton demonstrated through mathematical proof that all of Kepler’s laws were direct consequences of the law of gravity.
Kepler’s beliefs regarding the structure of the universe beyond our solar system were influenced by his mystical philosophy. He believed that the Sun remained motionless, with the sphere of stars serving as the boundary of the world. Kepler did not believe in the infinite expanse of the universe, and to support his argument, he proposed what would later be known as the photometric paradox. If the number of stars were infinite, then no matter which direction one looked, a star would always be visible, leaving no dark regions in the sky.
I have discovered that all celestial movements, both as a whole and in every individual case, are infused with a universal harmony – though not the exact one I had initially imagined, but an even more flawless one.
As an illustration, Kepler provides an explanation for why there are precisely six planets (at that time, only six planets of the solar system were known) and why they are positioned in space in their particular arrangement: it turns out that the planets’ orbits are inscribed within the correct polygons. Interestingly, based on these non-scientific considerations, Kepler made a prediction about the existence of two moons orbiting Mars and an intermediary planet located between Mars and Jupiter.
Kepler’s laws were a combination of clarity, simplicity, and computational power, but the mystical nature of his world system completely tainted the true essence of Kepler’s groundbreaking discoveries. However, even in Kepler’s time, his peers recognized the precision of these new laws, although their underlying significance remained unclear until Newton’s time. No one attempted to resurrect Ptolemy’s model or propose an alternative system of motion, aside from the heliocentric one.

Kepler was the original author of the comprehensive exposition of Copernican astronomy, which was published in three volumes under the title “Epitome Astronomiae Copernicanae” (1617-1622). This work was immediately banned and included in the Index of Prohibited Books. Kepler’s major contribution in this book was the description of all his astronomical discoveries.
In 1627, after 22 years of hard work, Kepler self-published a set of astronomical tables known as “Rudolf’s” in honor of the emperor. These tables were in high demand because the previous ones did not match up with observations. Notably, this was the first time logarithmic tables were included in such a work, making calculations more convenient. Kepler’s tables were used by astronomers and sailors until the early 19th century.
One year after Kepler passed away, Gassendi made an observation of Mercury’s anticipated crossing over the Sun’s disk. In 1665, an Italian physicist and astronomer named Giovanni Alfonso Borelli published a book confirming Kepler’s laws for the Jupiter satellites discovered by Galileo.
Kepler’s First Law (The Law of Ellipses)
Each planet within the solar system orbits in an elliptical shape with the Sun at one of its focal points. The shape of the ellipse and its similarity to a circle is determined by the ratio, where is the distance from the center of the ellipse to its focus (half of the interfocal distance), and is the major semi-axis. The value is known as the eccentricity of the ellipse. When , the ellipse becomes a perfect circle.
Kepler’s second law (the law of areas)
Each celestial body moves in a plane that passes through the central star, and over equal periods of time, the line segment connecting the star and the celestial body sweeps out equal areas.
Kepler’s third law (the harmonic law)
The squares of the orbital periods of celestial bodies around the central star are proportional to the cubes of the lengths of their major semi-axes. This relationship holds not only for planets, but also for their satellites.
Where T1 and T2 are the orbital periods of two celestial bodies around the central star, and a1 and a2 are the lengths of their major semi-axes.

Johannes Kepler.
From the original at the Royal Observatory in Berlin.
Johannes Kepler, also known as Kepler, was a renowned German astronomer who played a crucial role in the development of modern astronomy. Born in 1571, he is best known for his discovery of the laws of planetary motion, which are now commonly referred to as Kepler’s laws. These laws formed the basis for the creation of planetary tables, also known as Rudolph’s tables. Additionally, Kepler made significant contributions to the theory of eclipses. Notably, he is credited with inventing a telescope that utilized double-convex lenses for both the objective and eyepiece. The original works of Kepler can be found at the Royal Observatory in Berlin.
Johannes Kepler (December 27, 1571, Weilder-Stadt – November 15, 1630, Regensburg) was a German astronomer and mathematician who sought to find the mathematical harmony in the universe that was created by God. He worked on organizing the mathematical principles of Copernican ideas. Kepler studied at the University of Tübingen and later taught mathematics and ethics in Graz. He also created calendars and made astrological predictions.
In his work “Prodromus sive Mysterium cosmographicum” (Prodromus sive Mysterium cosmographicum, 1596), Kepler presented the divine mathematical order of the celestial bodies. He described how six planets corresponded to five distinct spaces, each represented by a “Platonic” polyhedron. Kepler served as a court mathematician in Prague and worked as an assistant to Tycho Brahe. Using Brahe’s precise observations of Mars, Kepler established the first two laws of planetary motion: the planets travel in elliptical orbits with the Sun at one of the foci, and the planets sweep out equal areas in equal times (“New Astronomy” – Astronomia nova, Pragae, 1609).
Later, Kepler extended these laws to include all planets and satellites. He also formulated the third law, known as the “Harmonies of the World” (Harmonices mundi, 1619), which states that the square of a planet’s orbital period is proportional to the cube of its average distance from the Sun. Kepler’s study on the “Stereometry of wine barrels” (1615) was particularly significant for mathematics, as he calculated the volumes of bodies obtained by rotating conical sections around an axis lying in the same plane.
Kepler also applied logarithms to create new tables of planetary motion (1627) and wrote the influential astronomy textbook “Epitome astronomiae Copernicanae” (1621). His discoveries had a profound impact on the philosophical and scientific development of the Renaissance and the Scientific Revolution.
New Philosophical Encyclopedia. In four volumes. / Institute of Philosophy of the Russian Academy of Sciences. Editorial Board: V.S. Stepin, A.A. Huseynov, G.Y. Semigin. Moscow, Mysl, 2010, vol. II, E – M, p. p. 242.
Johannes Kepler was born on December 27, 1571 in the town of Weil near Stuttgart in Germany. Kepler came from a humble background, and thus faced significant challenges in completing school and gaining admission to the University of Tübingen in 1589. While at the university, Kepler focused his studies on mathematics and astronomy. His mentor, Professor Mestlin, was a covert supporter of the Copernican theory. Inspired by his teacher, Kepler also became a proponent of the Copernican theory.
In 1596, Kepler released his work “Cosmographic Mystery,” which explored the relationship between the distances of planetary orbits and the radii of spheres inscribed with regular polyhedrons. This theory was based on Copernicus’ belief in the central position of the Sun in the planetary system. Although Kepler’s work still had elements of scholastic and quasi-scientific thinking, it garnered him considerable recognition.
In 1600, Tycho Brahe, the famous Danish astronomer-observer, arrived in Prague and offered Johannes a position as his assistant for observing the sky and making astronomical calculations. After Brahe passed away in 1601, Kepler began studying the remaining materials that contained data from past observations. Kepler eventually rejected the idea that planetary orbits were circular and instead proposed that they were elliptical. Through his calculations, he demonstrated that the planets do not travel in perfect circles, but rather in elliptical paths. Kepler’s first law states that the Sun is not located at the center of the ellipse, but at a specific point known as the focus. This means that the distance between a planet and the Sun is not constant. Kepler also discovered that a planet’s speed varies as it orbits the Sun: when a planet is closer to the Sun, it moves faster, and when it is farther away, it moves slower. This variation in the planets’ motion is known as Kepler’s second law.
In 1609, Kepler’s “New Astronomy” was published, which marked the introduction of both of his laws into the field of science. This publication laid the groundwork for the new field of celestial mechanics.
Kepler was drawn to the theory and practice of logarithms due to the need for improved astronomical calculations and the creation of tables based on the Copernican system. He developed the theory of logarithms from an arithmetic perspective and used it to compile logarithmic tables. These tables were first published in 1624 and remained in print until 1700.
In his work “Supplements to Vitellius, or the Optical Part of Astronomy” (1604), Kepler explored conic sections and presented the parabola as either a hyperbola or an ellipse with an infinitely distant focus. This was the first application of the principle of continuity in the history of mathematics.
During the time of the Thirty Years’ War, specifically from 1617 to 1621, when the Vatican had already banned Copernicus’s book, Kepler released three editions of “Essays on Copernican Astronomy”. Although the title may be misleading, as it suggests a focus on the Sun, the book actually discusses the position of the Sun as described by Copernicus, as well as the orbits of the planets, the Moon, and the recently discovered satellites of Jupiter according to Kepler’s own laws. In those same years, Kepler also published “Harmony of the World” where he introduced the third law of planetary motions, stating that the squares of the periods of revolution for two planets are proportional to the cubes of their average distances from the Sun.
Not only was Kepler involved in studying the movement of the planets, he also had an interest in other astronomical matters. One specific area that caught his attention was comets. Upon observing that the tails of comets always faced away from the Sun, Kepler speculated that these tails were formed as a result of the Sun’s rays. During that time, little was known about solar radiation and the structure of comets. It was only in the later half of the 19th century and the 20th century that it was established that the formation of comet tails is indeed linked to the radiation emitted by the Sun.
On November 15, 1630, Kepler passed away while traveling to Regensburg. He had made an unsuccessful attempt to receive at least a portion of the salary owed to him by the imperial treasury for many years.
Adapted from http://100top.ru/encyclopedia/
Additional resources:
Kepler’s Three Laws. In the publication: Gurtovtsev A.L. Think or Believe? Ode to the ignorance of human nature. Minsk, 2015.
Publications:
Collected Works, Vol. 1 – 18, edited by W. Van Dyck and M. Caspar. Munch., 1937-63; in Russian: A fresh perspective on the measurement of wine barrels. M,-L., 1935:
About the structure of hexagonal snowflakes. М., 1982.